Конспект лекций_Администрирование БД. Теоретические основы баз данных
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
1.3 Модели данных и этапы проектирования баз данных.Процесс проектирования БД представляет собой последовательность переходов от неформального словесного описания информационной структуры предметной области к формализованному описанию объектов предметной области в терминах некоторой модели. В общем случае можно выделить следующие этапы проектирования: Системный анализ и словесное описание информационных объектов предметной области и связей между ними. Как результат формулируется техническое задание на разработку базы данных. Проектирование инфологической модели предметной области в терминах некоторой семантической модели. Выбор конкретной СУБД и даталогическое или логическое проектирование БД. Декомпозиция отношений. Физическое проектирование БД, то есть выбор эффективного размещения БД на внешних носителях и способа доступа к ней. Способ описания данных и способ манипулирования данными определяют модель данных, поддерживаемую конкретной СУБД. Модель данных – это некоторая абстракция, которая, будучи приложима к конкретным данным, позволяет пользователям и разработчикам трактовать их уже как информацию, то есть сведения, содержащие не только данные, но и взаимосвязи между ними. Предметная область – часть реального мира, отражаемая в БД. Инфологическая (внешняя) модель данных – обобщённое, не привязанное к какой-либо ЭВМ или СУБД описание предметной области. Иногда говорят о нескольких внешних моделях данных, по-разному представляющих одну концептуальную модель. Отражает в удобной для разработчиков форме информационно-логический уровень абстрагирования, связанный с фиксацией и описанием объектов предметной области, их свойств и взаимодействий. Концептуальная модель данных – способ логического упорядочения данных (модели данных иерархическая, сетевая, реляционная, объектно-ориентированная). Даталогическая (внутренняя) модель данных – описание данных на языке конкретной СУБД. Физическая модель данных – описание расположения хранимых данных и методов доступа к ним (логическая структура файлов, работа с аппаратными средствами хранения данных)  Документальные модели данных соответствуют представлению о слабоструктурированной информации, ориентированной в основном на свободные форматы документов, например текстов на естественном языке или с гипертекстовой разметкой. Тезаурусные модели основаны на принципе организации словарей, содержат определенные языковые конструкции и принципы их взаимодействия в заданной грамматике. Эти модели эффективно используются в системах-переводчиках, особенно многоязыковых. Дескрипторные модели – самые простые из документальных моделей, они широко использовались на ранних стадиях использования документальных баз данных. В этих моделях каждому документу назначался дескриптор, который описывал документ по некоторым ключевым характеристикам. 1.4 Инфологическое моделирование. ER-диаграммы.Цель инфологического моделирования (ИМ) – обеспечение наиболее естественных для человека способов сбора и представления той информации, которую предполагается хранить в создаваемой базе данных. Инфологическое моделирование прежде всего связано с попыткой представления семаники предметной области в модели БД. Основным инструментом разработки инфологических моделей (прежде всего для реляционных баз данных) в настоящий момент являются диаграммы «сущность-связь» (Entity-Relationship). Предложен этот способ моделирования в 1976 г. Питером Пин-Шэн Ченом. В настоящее время используются различные нотации этой модели. Мы будем рассматривать ER-диаграммы в нотации Баркера. Конструктивные элементы инфологического моделирования: Сущность (Entity) – объект либо совокупность объектов, имеющих существенное значение для рассматриваемой предметной области, информация о которых подлежит хранению. Сущность имеет имя, уникальное в пределах моделируемой системы. С помощью сущности описывается класс однотипных объектов, т.е. предполагается, что в системе существует множество экземпляров данной сущности. Экземпляры сущности должны иметь некоторые уникальные признаки, позволяющие отличать их друг от друга. Сущность на диаграммах изображается в виде прямоугольника с наименованием. Атрибут сущности – этот некоторая характеристика экземпляра сущности, определяющая свойства данного представителя класса. При этом набор атрибутов должен быть таким, чтобы можно было различать конкретные экземпляры сущности. Например, атрибутами сущности «книги» могут являться «название», «количество страниц», «издательство», «цвет обложки». Атрибуты записываются внутри прямоугольника-сущности, по одному на строку. Ключ сущности – неизбыточный набор атрибутов, значения которых в совокупности являются уникальными для каждого экземпляра сущности. Неизбыточность заключается в том, что удаление любого атрибута из ключа должно приводить к нарушению его уникальности. Либо так: ключевым называют набор атрибутов, однозначно идентифицирующий конкретный экземпляр сущности. Атрибуты, входящие в ключ на диаграмме, выделяются подчёркиванием. Между сущностями могут быть установлены связи (relationship) – бинарные ассоциации, показывающие, каким образом сущности соотносятся или взаимодействуют между собой. Связь может существовать между двумя разными сущностями или между сущностью и ею же самой (рекурсивная связь). Связи всегда именуются. Связи делятся на три типа по множественности: - один-к-одному (1:1) – экземпляр одной сущности связан только с одним экземпляром другой сущности; - один-ко-многим (1:М) – один экземпляр сущности может быть связан с несколькими экземплярами другой сущности; - многие-ко-многим (М:М) – один экземпляр первой сущности связан с несколькими экземплярами второй сущности, и наоборот, один экземпляр второй сущности связан с несколькими экземплярами первой сущности. Пример – верхняя связь на рисунке: студенты слушают лекции многих преподавателей, и преподаватели читают лекции многим студентам. Следует отметить, что тип «многие ко многим» является временным типом связи, допустимым на ранних этапах разработки инфологической модели. В дальнейшем она заменяется на две связи (1:М) путём создания промежуточной сущности. В нашем случае это может быть сущность «расписание лекций». Другой пример – сущность «авторы» и сущность «книги». Некоторые книги написаны несколькими авторами, а некоторые авторы написали более одной книги. Для разрешения связи (М:М) необходима дополнительная сущность «титульная страница», содержащая в числе прочих атрибуты «название книги» и «фамилия автора». Связи также делятся на два типа по модальности: «обязательная» и «возможная». Связь является обязательной, если в ней должен участвовать каждый экземпляр сущности; возможной – если не каждый экземпляр сущности должен участвовать в связи. При этом связь может быть обязательной со стороны одной сущности и возможной со стороны другой. Пример – нижняя связь на рисунке: студент, пишущий диплом, всегда имеет научного руководителя, а преподаватель может иметь одного или несколько дипломников, или вовсе их не иметь. Графически связь изображается линией, соединяющей две сущности. Над линией помещается имя связи или два имени у каждого конца связи. Конец линии со стороны «многие» отмечается её растраиванием. В случае возможной связи линия пунктирная, в случае обязательной – сплошная.  В результате построения модели предметной области в виде набора сущностей и связей получается связный граф. В полученном графе не должно быть циклических связей – они выявляют некорректность модели. В ER-диаграмме допускается принцип категоризации сущностей. Это значит, что может вводиться подтип сущности, то есть сущность может быть представлена в виде нескольких подтипов, каждый из которых имеет некоторое подмножество атрибутов и отношений, наследуемых из основной сущности. В терминах ИМ: База данных – даталогическое представление информационной модели предметной области, а СУБД – система, с помощью которой реализуется централизованное управление данными, хранимыми в базе, доступ к ним и поддержание их в состоянии, соответствующем состоянию предметной области. 1.5 Модели доступа к данным.Помимо разделения баз данных по методам обработки, можно классифицировать их по используемой модели (или структуре) данных. С помощью модели данных можно наглядно представить структуру объектов и установленные между ними связи. Модель данных непосредственно определяет наименование СУБД. 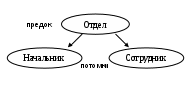 Иерархическая модель. БД состоит из упорядоченного набора древовидных структур данных. Организационные структуры, списки материалов, оглавления в книгах, планы проектов и многие другие совокупности данных могут быть представлены в иерархическом виде. При этом автоматически поддерживается целостность ссылок между предками и потомками. Основное правило: никакой потомок не может существовать без своего родителя, причём потомок имеет единственного родителя. Недостатком модели является сложность реорганизации данных и невозможность выполнения «горизонтальных» запросов к данным, не связанных с иерархической структурой. Иерархическая модель появилась первой среди всех даталогических моделей: именно эту модель поддерживала первая из зарегистрированных промышленных СУБД IMS (Information Management System) IBM (1968 год). Каждая физическая база описывается набором операторов, определяющих как её логическую структуру, так и структуру хранения баз данных. С 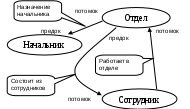 предок етевая модель. Является расширением иерархической модели. Здесь каждый порождённый элемент (потомок) может иметь более одного порождающего элемента (предка). Сетевая БД может представлять непосредственно все виды связей, присущих данным. По этим данным можно перемещаться, исследовать и запрашивать их всевозможными способами. Однако любой запрос к сетевой БД предполагает выработку собственного механизма навигации по этой базе. При этом автоматически целостность данных СУБД не поддерживается. Базовыми понятиями модели являются: Элемент данных – минимальная информационная единица, доступная пользователю с использованием СУБД. Агрегат – поименованный набор данных. Агрегат данных типа «вектор» - линейный набор элементов данных (например агрегат «Адрес: город, улица, дом, квартира»). Агрегат данных типа «повторяющаяся группа» соответствует совокупности векторов данных. Например, агрегат «Зарплата: месяц, сумма (х 12)». Записью называется совокупность агрегатов или элементов данных, моделирующая некоторый класс объектов реального мира. Для записи вводятся понятия типа записи и экземпляра записи. Связь или набор – двухуровневый граф, связывающий отношением «один-ко-многим» два типа записи. Связи именуются. Для любых двух типов записей может быть задано любое количество связей. Некоторые правила и термины построения сетевой модели: Тип связи L определяется для типа записи предка P и потомка C. Экземпляр типа связи состоит из одного экземпляра типа записи предка и упорядоченного набора экземпляров типа записи потомка. При этом (1) каждый экземпляр типа P является предком только в одном экземпляре L; (2) Каждый экземпляр C является потомком не более чем в одном экземпляре L. Следствия таких правил таковы: Тип записи С в связи L1 может быть типом записи P в связи L2 (обычная иерархическая модель). Тип записи P может быть таковым в любом числе типов связи. Тип записи P может фигурировать как тип записи C в любом числе типов связи. Может существовать любое число типов связи с одним и тем же типом записи P и типом записи C. Одни и те же типы записей могут быть предком и потомком в связи L1 и потомком и предком в связи L2. Стандарт сетевой модели впервые был определен в 1975 году организацией CODASYL (Conference of Data System Language), которая определила базовые понятия модели и формальный язык описания. Типичным представителем является Integrated Database Management System (IDMS) компании Cullinet Software, Inc. Реляционная модель. Основная идея реляционной модели данных заключается в том, чтобы представить любой набор данных в виде двумерной таблицы. В простейшем случае реляционная модель описывает единственную двумерную таблицу, но чаще всего эта модель описывает структуру и взаимоотношения между несколькими таблицами. Реляционная модель не позволяет корректно представить данные, имеющие собственную сложную структуру. Создание реляционных отношений для таких данных может привести к потере значимых связей между данными. Примеры широко известных реляционных БД: MS FoxPro, MS Access. Объектно-ориентированная модель. Её структура описывается с помощью трёх ключевых понятий: Инкапсуляция – каждый объект хранит в себе набор данных (т.е. обладает некоторым внутренним содержанием) и набор методов, с помощью которых (точнее исключительно с помощью которых) можно получить доступ к данным этого объекта. Наследование – подразумевает возможность создавать из классов объектов новые классы объектов, которые наследуют структуру и методы своих предков, добавляя к ним (или исключая) структуру данных и методы, отражающие их собственную индивидуальность. Полиморфизм – различные объекты в зависимости от внешних событий могут вызывать одинаково названные методы, но по-разному реализованные. Особенностью ООБД является невозможность применения к хранимым объектам понятий и алгоритмов реляционной модели. В этой связи необходим некоторый процедурный язык для оформления запросов и обработки данных. Обеспечение целостности данных заключается в (1) автоматической поддержке отношений наследования; (2) возможности объявлять поля и методы объекта как «скрытые» (т.е. невидимые для других объектов); (3) реализовывать процедуры контроля целостности данных внутри объектов. Примеры ООБД: Caché, FastObjects, GemStone/S, Jasmine, к ним примыкает объектно-реляционная СУБД PostgeSQL. 1.6 Теория модели реляционных баз данных.Теоретической основой модели стала теория отношений, основу которой заложили Ч.С. Пирс и Э. Шрёдер. Основоположником теории реляционных баз данных считается сотрудник фирмы IBM доктор A. Codd, опубликовавший в 1970 г. статью «Реляционная модель данных для больших коллективных банков данных». Кодд, будучи математиком по образованию, предложил использовать для обработки данных аппарат теории множеств и предикативной логики для того, чтобы внести в область управления базами данных строгие математические принципы. Предложения Кодда были настолько эффективны для систем баз данных, что за эту модель он был удостоен премии Тьюринга в области теоретических основ вычислительной техники. Термины реляционной модели и теории множеств: Домен (Domain) – некоторое конечное множество. Обозначение: Di , где i – номер домена. Отдельный элемент домена обозначим di с тем же смыслом i. Полное декартово произведение множеств – набор всевозможных сочетаний из n элементов каждое, где каждый элемент берётся из своего домена. Описание: D1D2…Dn. Отношение (relation) R – подмножество декартова произведения множеств D1, D2, … Dn (n≥1), необязательно различных. Описание: R D1D2…Dn. Число n называется степенью отношения (n = 1 – унарное, n = 2 – бинарное, в общем случае n-арное). Атрибутом (Attribute) называют домен, входящий в отношение. Степень отношения определяет количество атрибутов в отношении. Кортежем (Tuple) называют декартово произведение элементов множеств d1d2…dn. Атрибуты, значения которых однозначно идентифицируют кортежи, называются ключевыми. Отношение может содержать несколько ключей. Всегда один из ключей объявляется первичным (primary key), его значения не могут обновляться. Все остальные ключи отношения называются возможными (потенциальными) ключами. Схемой отношения S называется перечень имён атрибутов данного отношения с указанием домена, к которому они относятся. Описание: SR= (A1, A2, …, An), Ai Di. Набор именованных схем отношений представляет собой схему базы данных. Отношения удобно представлять в виде таблиц. Можно условно связать язык формальной логики, язык инфологических моделей и практический язык терминов реляционных БД с помощью следующей таблицы «синонимов»:
В прикладном смысле реляционной считается такая база данных, в которой все данные представлены для пользователя в виде прямоугольных таблиц значений данных, и все операции над базой данных сводятся к манипуляциям с таблицами. В более строгом изложении реляционная модель состоит из трех частей, описывающих разные аспекты реляционного подхода: структурной части, манипуляционной части и целостной части. 1. В структурной части модели фиксируется, что единственной структурой данных, используемой в реляционных БД, является нормализованное n-арное отношение. 2. В манипуляционной части модели утверждаются два фундаментальных механизма манипулирования реляционными БД: реляционная алгебра и реляционное исчисление. 3. В целостной части реляционной модели данных фиксируются два базовых требования целостности, которые должны поддерживаться в любой реляционной СУБД: требование целостности сущностей и требование целостности по ссылкам. Свойства реляционных баз данных (вытекают из определения отношения и кортежа как множеств): В отношении нет одинаковых кортежей (все строки таблицы различаются по своему содержанию). Следствие: наличие у каждого кортежа первичного ключа. Для каждого отношения, по крайней мере, полный набор его атрибутов является первичным ключом. Однако, при определении первичного ключа должно соблюдаться требование "минимальности", т.е. в него не должны входить те атрибуты, которые можно отбросить без ущерба для основного свойства первичного ключа - однозначно определять кортеж. Отсутствие упорядоченности кортежей (таблица с переставленными строками остаётся той же самой таблицей). Отсутствие упорядоченности атрибутов (таблица с переставленными столбцами остаётся той же самой таблицей). Все значения атрибутов отношения атомарные (в каждой позиции на пересечении столбца и строки расположено только одно значение). Последнее свойство является одним из самых спорных, и практически никогда не реализуется. Во всех широко распространённых СУБД используется в качестве значения поля маркер NULL, означающий отсутствие информации и обрабатывающийся специальным образом. Правило целостности объектов говорит о том, что первичный ключ отношения не должен содержать значений NULL. Реляционная алгебра: Алгеброй называется множество объектов с заданной на нём совокупностью операций, замкнутых относительного этого множества. Коддом было предложено 8 операций, хотя это множество избыточное, так как некоторые операции могут быть представлены друг через друга. Теоретико-множественные операции: Объединение отношений. Результатом объединения двух отношений является отношение, включающее все кортежи, входящие хотя бы в одно из отношений-операндов. Обозначение: R3 = R1 R2. Операция коммутативна. Пересечение отношений. Результатом пересечения двух отношений является отношение, включающее все кортежи, входящие в оба отношения-операнда. Обозначение: R3 = R1 R2. Операция коммутативна. Разность отношений. Отношение, являющееся разностью двух отношений включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом. Обозначение: R3 = R1 \ R2. Операция некоммутативна. Пример на первые три операции: Предметная область: экзамен по курсу «Методы вычислений», который проводился в сентябре и декабре. Пусть имеются три отношения, имеющие эквивалентные схемы: R1 = (Номер зачетки, ФИО, Группа) – список студентов, сдававших экзамен в сентябре; R2 = (Номер зачетки, ФИО, Группа) – список студентов, сдававших экзамен в декабре; R3 = (Номер зачетки, ФИО, Группа) – список студентов, сдавших экзамен по курсу до января месяца; Ударим реляционной алгеброй по следующим вопросам: а) Какие студенты сдавали два раза, но так и не сдали экзамен? Ответ: R = R1 R2 \ R3. б) Какие студенты сдавали экзамен только один раз, и сдали его? Ответ: R = (R1 \ R2 R3) (R2 \ R1 R3). в) Какие студенты смогли сдать экзамен только со второго раза? Ответ: R = R1 R2 R3. г) Какие студенты сдавали экзамен один раз, не сдали, и больше не появлялись? Ответ: R = (R1 \ R2) (R2 \ R1) \ R3. Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами. Прямое произведение отношений (расширенное декартово произведение). Результатом прямого произведения двух отношений является отношение, кортежи которого являются конкатенацией (сцеплением) кортежей первого и второго операндов. Обозначение: R1 R2. Операция коммутативна. Операция используется для получения отношения, которое характеризует все возможные комбинации между элементами отдельных множеств. Специальные реляционные операции: Ограничение отношения (горизонтальная фильтрация). Результатом ограничения отношения по некоторому условию является отношение, включающее кортежи отношения-операнда, удовлетворяющее этому условию. Обозначение: R[(r)], где - булевское выражение, составленное из термов сравнения с помощью связок «И», «ИЛИ», «НЕ» и скобок. Унарная операция. На интуитивном уровне операцию ограничения лучше всего представлять как взятие некоторой "горизонтальной" вырезки из таблицы. Пример: выбрать из R3 студентов из группы 21402. Запишем так: R4 = R3 [Группа = 21403]. Проекция отношения (вертикальная фильтрация). Результатом проекции отношения R на заданный набор его атрибутов B является отношение, кортежи которого производятся путем взятия соответствующих значений из кортежей отношения-операнда. Обозначение: R[B]. Значения, не принадлежащие атрибутам из набора В, удаляются. Унарная операция. Продолжаем наш пример: R = R4[Номер зачетки, ФИО]. Соединение отношений (соединение по условию). При соединении двух отношений R и Q по некоторому условию образуется результирующее отношение, кортежи которого являются конкатенацией кортежей первого и второго отношений и удовлетворяют этому условию. Обозначение: R []Q. По определению результатом операции сравнения является отношение, получаемое путем выполнения операции ограничения по условию прямого произведения отношений R и Q. Операция соединения называется операцией эквисоединения, если условие соединения имеет вид (a = b), где a и b - атрибуты разных операндов соединения. Такое соединения применяется к паре отношений R и Q, обладающих общим атрибутом (т.е. атрибутом с одним и тем же именем и определенным на одном и том же домене). На интуитивном уровне это способ связи таблиц, имеющих одинаковое по смыслу поле. Деление отношений. Пусть заданы два отношения – R(a1, a2, ..., an, b1, b2, ..., bm) и T(b1, b2, ..., bm). Будем считать, что атрибут bi отношения R и атрибут bi отношения T не только обладают одним и тем же именем, но и определены на одном и том же домене. Назовем множество атрибутов {aj} составным атрибутом A, а множество атрибутов {bj} - составным атрибутом B. После этого будем говорить о реляционном делении бинарного отношения R(A,B) на унарное отношение T(B). Результатом деления является унарное отношение Q(A), состоящее из таких кортежей v, которые в отношении R фигурировали как кортежи-сцепления Предположим, что имеются два отношения: Студенты(Имя, Группа) и Имена(Имя), причем унарное отношение Имена содержит все имена студентов в университете. Тогда после выполнения операции реляционного деления отношения Студенты на отношение Имена будет получено унарное отношение, содержащее номера групп, в которых студенты обладают всеми возможными в университете именами. 1.7 Ключи и поддержка целостности.Возможным (потенциальным) ключом отношения называется набор атрибутов, однозначно определяющий кортеж отношения, причём при удалении любого атрибута из этого набора его свойство однозначной идентификации кортежа теряется. Потенциальный ключ должен иметь следующие свойства: - уникальность (на практике – обязательное условие); - неизбыточность (на практике – может быть нарушено); В общем случае в отношении может быть несколько возможных ключей. Среди всех возможных ключей отношения обычно выбирают один, который считается главным, и который называют первичным ключом отношения. Неключевым атрибутом называется любой атрибут отношения, не входящий в состав ни одного возможного ключа. Атрибут, не входящий в состав первичного ключа, назовём непервичным. Различные объекты предметной области, информация о которых хранится в базе данных, всегда взаимосвязаны друг с другом. Например, накладная на поставку товара содержит список товаров с количествами и ценами, сотрудник предприятия имеет детей, числится в подразделении и т.д. Термины "содержит", "имеет", "числится" отражают взаимосвязи между понятиями. Такие взаимосвязи отражаются в реляционных базах данных при помощи внешних ключей(foreignkey), связывающих несколько отношений. Пусть дано отношение R. Подмножество атрибутов А отношения R будем называть внешним ключом, если: Существует отношение S (R и S не обязательно различны) с потенциальным ключом K. Каждое значение A в отношении R всегда совпадает со значением K для некоторого кортежа из S, либо является null-значением. Отношение S называется родительским отношением, отношение R называется дочерним отношением. Под целостностью реляционной базы данных будем понимать соответствие информационной модели предметной области, хранимой в базе данных, объектам реального мира и их взаимосвязям в каждый момент времени. 1. Правило структурной целостности: допускается работа только с однородными структурами данных типа «реляционное отношение». 2. Правило целостности объектов: первичный ключ отношения не должен содержать значений NULL. 3. Правило языковой целостности: реляционная СУБД должна обеспечивать языки описания и манипулирования данными не ниже стандарта SQL. Ссылочная целостность обеспечивает поддержку непротиворечивого состояния базы данных в процессе модификации данных при выполнении операций добавления или удаления. 4. Правило ссылочной целостности (declarative referential integrity): база данных не должна содержать значений внешних ключей, для которых не существует соответствующих значений потенциальных ключей. Поддерживается один из двух принципов взаимосвязи между экземплярами кортежей взаимосвязанных отношений: - кортежи подчинённого отношения уничтожаются при удалении кортежа основного отношения, связанного с ними. - кортежи основного отношения модифицируются при удалении кортежа основного отношения, связанного с ними, при этом на месте ключа родительского отношения ставится значение NULL. Для внешнего ключа характерны следующие свойства: - Каждое значение атрибута внешнего ключа должно являться значением соответствующего потенциального ключа. Причём обратное необязательно. - Количество атрибутов внешнего ключа должно соответствовать количеству атрибутов потенциального ключа. Если внешний ключ – составной, то и потенциальный – составной. - Для внешнего ключа не требуется, чтобы он был компонентом первичного ключа или вообще какого-либо потенциального ключа в отношении, к которому он принадлежит. - Каждый атрибут, входящий в данный внешний ключ, должен быть пределен на том же домене, что и соответствующий атрибут потенциального ключа. - Для атрибутов внешнего ключа разрешается иметь значение NULL. В общем случае запрещение реальной СУБД при проверке условия ссылочной целостности изменять или удалять значения первичного ключа называется ограничением (restrict). Отображение изменений или удалений значений первичного ключа на соответствующих значениях внешнего ключа называется каскадированием (cascading). 1.8 Нормализация отношений в базе данных.Классическая технология проектирования реляционных баз данных связана с теорией нормализации, основанной на анализе функциональных зависимостей между атрибутами отношений. Функциональной зависимостью набора атрибутов B отношения R от набора атрибутов А того же отношения называется такое соотношения проекций1 R[A] и R[B], при котором в каждый момент времени любому элементу проекции R[A] соответствует только один элемент проекции R[B], входящий вместе с ним в какой-либо кортеж отношения R. Обозначение: R.A R.B Взаимно-независимые – атрибуты, которые не зависят функционально друг от друга. Аксиомы функциональных зависимостей: Рефлексивность: если B А, то А B. Дополнение: если А B, то АС BС. Транзитивность: если А B и B C, то А С. Проектирование схемы базы данных обычно осуществляется путём декомпозиции (разбиения) исходного набора отношений, при этом полученные отношения являющихся проекциями исходных. Схемы базы данных называются эквивалентными, если содержание исходной базы может быть получено путём естественного соединения отношений, входящих в результирующую схему, и при этом не появляется новых кортежей в исходной базе данных. Нормализация – это процесс проектирования схемы базы данных с использованием декомпозиции. Каждой нормальной форме соответствует некоторый определённый набор ограничений, и отношение находится в некоторой нормальной форме, если удовлетворяет свойственному ей набору ограничений. 1NF . Отношение находится в первой нормальной форме тогда и только тогда, когда значения всех его атрибутов атомарны. Это определение является синонимом определения отношения в теории реляционных баз данных. Пример отношения, которое НЕ находится в 1NF: расписание занятий
Для перевода отношения в 1NF необходимо разделить с дублированием содержания общие ячейки на отдельные записи. 2NF . Отношение находится во второй нормальной форме тогда и только тогда, когда оно находится в первой нормальной форме и не содержит неполных функциональных зависимостей непервичных атрибутов от атрибутов первичного ключа. Функциональная зависимость R.A R.B называется полной, если набор атрибутов В функционально зависит от А, но не зависит функционально от любого подмножества А, то есть если А1 А R.A –/ R.B. В противном случае функциональная зависимость называется неполной. Пример отношения, которое НЕ находится во 2NF: результаты сессии. Рассмотрим отношение R ( ФИО, номер зачетки, группа, дисциплина, оценка ). Первичный ключ подчеркнут. Однако при этом атрибуты (ФИО, группа) зависят только от части первичного ключа – от атрибута (номер зачетки). При этом возможны следующие аномалии: - в результате ошибки оператора студенту по результатам одного или нескольких экзаменов приписали не ту группу. - если студент не сдал ни одного экзамена, то он не существует. Для приведения отношения во 2NF следует провести декомпозицию (разбить на проекции), например так: R1 ( ФИО, номер зачетки, группа). R2 (номер зачетки, дисциплина, оценка ). Приведение таблицы ко второй нормальной форме позволяет избежать повторения (избыточности) данных. 3NF . Отношение находится в третьей нормальной форме тогда и только тогда, когда оно находится во второй нормальной форме и не содержит транзитивных зависимостей. Функциональная зависимость R.A R.B является транзитивной, если существует набор атрибутов C такой, что: С не является подмножеством А. С не включает в себя В. (В С) Существует функциональная зависимость R.A R.С. Не существует функциональной зависимости R.С R.А. Существует функциональная зависимость R.С R.B. Иными словами, требование 3NF сводится к тому, чтобы все неключевые поля зависели только от первичного ключа и не зависели друг от друга. Пример отношения, которое находится во 2NF, но НЕ находится в 3NF: связь студента с группой, факультетом, специализацией. Дано отношение: R( номер зачетки, ФИО, группа, факультет, кафедра ). Первичный ключ подчеркнут. Так как он состоит из одного атрибута, то критерий 2NF выполнен. В отношении имеются транзитивные зависимости, в числе которых: 1) номер зачётки группа (обратное неоднозначно), группа факультет, номер зачётки факультет. 2) номер зачётки кафедра, кафедра факультет, номер зачётки факультет. Для приведения отношения в 3NF требуется декомпозиция следующего вида: R1 ( номер зачетки, ФИО, группа ). R2 ( группа, факультет). R3 (кафедра, факультет ). BCNF . Отношение находится в нормальной форме Бойса-Кодда, если оно находится в третьей нормальной форме и каждый детерминант отношения является возможным ключом этого отношения. Определение: Если в отношении существует несколько функциональных зависимостей, то каждый атрибут или набор атрибутов, от которого зависит другой атрибут, называется детерминантом отношения. Иными словами, отношение находится в BCNF, если любая функциональная зависимость между его атрибутами сводится к полной функциональной зависимости от возможного ключа. Пример отношения, которое находится в 3NF, но НЕ находится в BCNF: таблица результатов приемных экзаменов: Дано отношение: R( идентификатор, номер паспорта, предмет, оценка ). Ответ на вопрос: зачем? Например, один абитуриент потерял свою карточку и ему выдали другую с другим номером. Второй абитуриент – гениальный ребенок, и у него пока нет паспорта. Имеются следующие функциональные зависимости: 1. Идентификатор, предмет оценка; 2. Номер паспорта, предмет оценка; (зависимость полная) 3. Идентификатор номер паспорта; (зависимым не является непервичный атрибут) 4. Номер паспорта идентификатор. Транзитивных зависимостей нет, так как зависимость 3 имеет обратную 4. Таким образом, отношение находится в 3NF. Но функциональные зависимости между атрибутами идентификатор и номер паспорта не являются зависимостями от возможного ключа этого отношения. Для приведения отношения в BCNF возможна декомпозиция следующего вида: R1 ( идентификатор, предмет, оценка). R2 ( идентификатор, номер паспорта). Ответ на вопрос: зачем? Например, один абитуриент потерял свою карточку и ему выдали другую с другим номером. Второй абитуриент – гениальный ребенок, и у него пока нет паспорта. В большинстве случаев достижение третьей нормальной формы или даже формы Бойса-Кодда считается достаточным для реальных проектов баз данных, однако в теории нормализации существуют и другие нормальные формы: 4NF. Отношение находится в четвёртой нормальной форме в том и только в том случае, если существует многозначная зависимость А –>> B и все остальные атрибуты R функционально зависят от А. Определение: В отношении R(A,B,C) существует многозначная зависимость R.A –>> R.B в том и только в том случае, если множество значений В, соответствующее паре значений атрибутов А и С, зависит только от А и не зависит от С. Иными словами, отношение находится в четвёртой нормальной форме, если оно находится в BCNF, и все его многозначные зависимости являются функциональными зависимостями от потенциальных ключей. Пример (1) отношения, которое НЕ находится в 4NF: список дисциплин, которые предстоит прослушать студенту первого курса: Дано отношение: R( номер зачетки, группа, дисциплина ). Перечень дисциплин, которые должен слушать студент на первом курсе, определяется исключительно номером группы, а не номером зачетки. То есть, в данном отношении существуют две многозначные зависимости: группа –>> дисциплина. группа –>> номер зачетки. Это означает, что каждой группе однозначно соответствует перечень дисциплин по учебному плану, и номер группы определяет список студентов, которые в этой группе учатся. При этом возможны следующие аномалии: - Мы не можем хранить информацию о новой группе и перечне её дисциплин до тех пор, пока в неё не будут зачислены студенты. - Если в группу добавляется новый студент, то необходимо сгенерировать для него весь перечень дисциплин для данной группы. Для приведения отношения в 4NF возможна декомпозиция следующего вида: R1 ( номер зачетки, группа). R2 (группа, дисциплина ). Пример (2): меню: Исходное отношение: R( блюдо, повар, рецепт ). Повар умеет готовить разные блюда, одинаково названные блюда могут отличаться рецептом приготовления. Декомпозиция: R1 ( повар, блюдо). R2 (блюдо, рецепт). 5NF (PJ/NF). Отношение R находится в пятой нормальной форме (нормальной форме проекции-соединения) в том и только в том случае, когда любая зависимость соединения в R следует из существования некоторого возможного ключа в R. Определение: Отношение R (A, B, … Z) удовлетворяет зависимости соединения (А, B, … Z) в том и только в том случае, когда R восстанавливается без потерь путём соединения своих проекций на A, B, … Z (наборы атрибутов отношения R). Полной декомпозицией отношения называют такую совокупность произвольного числа его проекций, соединение которых полностью совпадает с содержимым исходного отношения. Иными словами, отношение находится в пятой нормальной форме тогда и только тогда, когда в каждой его полной декомпозиции все проекции содержат возможный ключ. Пример отношения, которое находится в 4NF, но НЕ находится в 5NF: почасовики. Дано отношение: R( преподаватель, кафедра, дисциплина). Считается, что приглашённый преподаватель может работать на нескольких кафедрах и вести различные дисциплины. В этом случае ключом отношения является полный набор из трёх атрибутов. В отношении отсутствуют многозначные зависимости, и поэтому оно находится в 4NF. Однако в нём нет наборов атрибутов, которые составляют возможные ключи отношения, и потому это отношение не в PJ/NF. При этом провести полную декомпозицию на два отношения нельзя. Возможна декомпозиция следующего вида: R1 ( преподаватель, кафедра). R2 (преподаватель, дисциплина ). R3 (кафедра, дисциплина). Отношение, не имеющее ни одной полной декомпозиции, также находится в пятой нормальной форме. |
