Теоретические основы термоконтактного пиролиза

• Название: Теоретические основы термоконтактного пиролиза
• Дата: 25.11.2022
• Размер: 1.11 Mb.
• Имя файла: Rgr_8_Variant (2).docx
• Тип: Документы; #811997

1. 
   Теоретические основы термоконтактного пиролиза
   

В настоящее время нефтехимический потенциал промышленно развитых государств определяется объемами производства низших олефинов. Практически весь этилен получают в процессе термического пиролиза. Этот процесс представляет собой модификацию термического крекинга нефтепродуктов, развитие которого с применением трубчатых печей началось в 10 ‒ 20-x гг. на нефтеперерабатывающих заводах США. Первые промышленные синтезы современной нефтехимии были осуществлены на основе этилена и пропилена, выделенных из газов крекинга.

Первые установки термического пиролиза в трубчатых печах, специально предназначенные для производства низших олефинов, были сооружены в США в 30-x г.; в странах Западной Европы, Японии и СССР они появились в 40 ‒ 50-x г. В 60-e годы в технологическую схему производства низших олефинов был внесен ряд важных усовершенствований. Углубление знаний основных закономерностей процесса позволила перейти к новым конструкциям печей, с применением которых был осуществлен пиролиз при высоких температурах и малом времени пребывания сырья в реакционной зоне. Освоение жестких режимов процесса в печах с вертикально расположенными трубами резко повысило удельные выходы этилена. В технологическую схему был введен, так называемый, узел «закалки» пирогаза, что позволило использовать тепло продуктов пиролиза для выработки пара высокого давления. Наличие на установках пара собственного производства обеспечило на стадии сжатия пирогаза экономически эффективную замену компрессоров с электрическим приводом на турбокомпрессоры.

Пиролиз ‒ процесс термического превращения углеводородов (предпочтительно парафиновых) при быстром повышении температуры сырья до 750 ‒ 900 °С (вплоть до 1200 °С при пиролизе метана) и низком давлении до 0,03 ‒ 0,12 МПа за время реакции 0,1 ‒ 0,3 с в присутствии перегретого водяного пара и следующим за этим мгновенным понижением температуры продуктов реакции до 370 ‒ 420 °С в течение 0,02 ‒ 0,03 с [6].

Газообразное сырье ‒ этан, пропан, н-бутан и их смеси ‒ является наилучшим сырьем с точки зрения получения максимальных выходов этилена и пропилена. Состав продуктов пиролиза этого сырья зависит от глубины конверсии (степени превращения), которая в промышленной практике определяется конкретными условиями производства: необходимостью выработки заданного объема продуктов, загруженностью узла компримирования и системы газоразделения, энергетическими затратами и др.

Подаваемый на пиролиз пропан обычно имеет концентрацию 99 % и в качестве примесей в нем присутствуют этан и бутан. В промышленных условиях степень превращения пропана достигает 85 ‒ 90 %. По сравнению с этаном выход этилена при пиролизе пропана в 2 раза ниже в расчете на полную конверсию сырья. Однако пропан дает высокий выход пропилена, который при невысоких степенях превращения может составлять 18 ‒ 19 %, а с учетом рецикла ‒ до 23 %

2. 
   Краткое описание технологического объекта
   

Основным аппаратом установки процесса пиролиза является реактор (трубчатый реактор – печь пиролиза).

1. 
   Описание процесса пиролиза
   

В реакторах пиролиза происходят различные термические превращения углеводородного сырья с получением водорода, этилена, пропилена, метана, бутадиена, бутиленов, бензола, смолистых продуктов, кокса и других продуктов. Для обеспечения стабильной работы печи пиролиза необходимо поддерживать оптимальные параметры процесса, обеспечивающие требуемые выходы продуктов.

Пиролиз представляет собой сложный процесс химических реакций, делящихся на первичные и вторичные реакции. К первичным реакциям относятся реакции расщепления (крекинга) молекул парафиновых и нафтеновых углеводородов с получением этилена, пропилена, метана, этана, водорода. Вторичные реакции – это в основном превращения типа конденсации и полимеризации, в результате которых из непредельных углеводородов получаются диолефины, а в дальнейшем ароматические углеводороды.

Образование кокса при пиролизе является результатом вторичных реакций конденсации и полимеризации. Как в ходе первичных, так и вторичных превращений протекают реакции дегидрирования. Все превращения, протекающие при пиролизе, имеют свободно-радикальный характер, механизм превращения – цепной.

Пиролиз н–гексана:

С₆Н₁₄ = С₂Н₄ + С₄Н₁₀

С₆Н₁₄ = С₃Н₈ + С₃Н₆

С₆Н₁₄ = С₆Н₁₂ + Н₂

С₆Н₁₄ = СН₄ + С₅Н₁₀

С₆Н₁₄ = С₄Н₈ + С₂Н₆

В дальнейшем полученные предельные углеводороды в свою очередь разлагаются:

С₃Н₈ = СН₄ + С₂Н₄

С₃Н₈ = С₃Н₆ + Н₂

С₄Н₁₀ = С₂Н₄ + С₂Н₆

С₄Н₁₀ = С₃Н₆ + СН₄

С₄Н₁₀ = С₄Н₈ + Н₂

С₂Н₆ = С₂Н₄ + Н₂

Пиролиз циклогексана. Первичные реакции:

С₆Н₁₂ = С₄Н₆ + С₂Н₆

С₆Н₁₂ = С₄Н₆ + Н₂ + С₂Н₄

С₆Н₁₂ = С₆Н₆ + 3Н₂

Вторичные реакции (общие для обоих исходных углеводородов):

С₂Н₄ = С₂Н₂ + Н₂

2С₂Н₄ = С₄Н₆ + Н₂

С₂Н₄ + С₄Н₆ = С₆Н₆ + 2Н₂

С₂Н₄ + С₆Н₆ = С₆Н₅ + С₂Н₅

С₆Н₅ + С₂Н₅ + С₂Н₄ = С₆Н₄(С₂Н₅)₂

С₆Н₄ + (С₂Н₅)₂ = С₁₀Н₈ + 3Н₂ и т.д.

Чем выше температура пиролиза, тем выше конверсия сырья. Если меняется состав сырья, предпочтительно поддерживать заданную температуру в реакторе, чтобы поддерживать постоянной относительную жесткость пиролиза.

Основные входные и выходные переменные реактора приведены на рисунке 1. Обычно на протекание процесса пиролиза воздействуют изменением расхода сырьевой смеси и температуры в реакторе. Таким образом, основными регулируемыми входными переменными реактора, влияющими на процесс пиролиза, являются Q, T.

Основные выходные переменные реактора: Y_ол – выход суммы олефинов; Y_э – выход этилена; Y_п – выход пропилена; Y_б – выход суммы бутиленов.

Основными статическими характеристиками реактора являются:

1 зависимость Y_ол = f(T, Q);

2 зависимость Y_э = f(T, Q);

3 зависимость Y_п = f(T, Q);

4 зависимость Y_б = f(T, Q).

Исследуемый объект (реактор) представлен в виде аналитической математической модели.


T – температура в реакторе; Q – расход сырьевой смеси; Q_вп – расход водяного пара; C – состав сырья; T_c – температура сырья на входе в реактор; T_вп – температура водяного пара на входе в реактор; Y_ол – выход суммы олефинов; Y_э – выход этилена; Y_п – выход пропилена; Y_б – выход суммы бутиленов

Рисунок 1 – Схема модели реактора

2. 
   Описание компьютерной модели процесса пиролиза
   

Математическое моделирование в последнее время становится все более эффективным методом научного исследования, основанным на познании изучаемого химико-технологического процесса с помощью математической модели. Моделирование и расчеты процессов и химических реакторов связаны с необходимостью выбора наилучшего варианта из многих возможных.

Моделирующая компьютерная программа представляет собой документ электронной таблицы Excel, с программным приложением Visual Basic и пред-назначена для моделирования и расчёта процесса термоконтактного и термокаталитического разложения углеводородов в лифт-реакторах в температурном ин-тервале от 450 до 800 °С. Расчёт производиться совместно лифт-реактора и регенератора.

Структурная схема реакторно-регенераторного блока процесса пиролиза приведена на рисунке 2, где при моделировании вводятся основные входные и выводятся выходные переменные.

В математическую модель реакторного блока входят: математические модели лифт-реактора пиролиза и регенератора микросферического катализатора (контакта) в кипящем слое.

Уравнения, входящие в моделирующий алгоритм, связывают между собой материальные, тепловые, химические, гидродинамические, конструктивные и другие параметры.

Материальные и соответствующие им тепловые балансы реактора и регенератора составляют основу алгоритма расчета.

Тепловой баланс реактора:

;

тепловой баланс регенератора: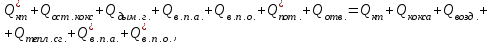

где Q*_кт – количество тепла, уносимое из регенератора и вносимое в реактор катализатором;

Q_{ост.кокс} – количество тепла, уносимое из регенератора и вносимое в реактор коксом;

Q_кт – количество тепла, уносимое из реактора и вносимое в регенератор катализатором;

Q_кокса – количество тепла, уносимое из реактора и вносимое в регенератор коксом;

Q*_вп – количество тепла, вносимое в реактор водяным паром;

Q_вп – количество тепла, уносимое из реактора водяным паром;

Q_в.п.а – количество тепла, вносимое в регенератор водяным паром, адсорбированным на катализаторе;

Q*_в.п.а – количество тепла, уносимое из регенератора водяным паром, адсорбированным на катализаторе;

Q_в.п.о – количество тепла, вносимое в регенератор водяным паром, подаваемым на отпарку;

Q*_в.п.о. – количество тепла, уносимое из регенератора водяным паром, подаваемым на отпарку;

Q_дым.г – количество тепла, уносимое из регенератора дымовыми газами регенерации;

Q_возд – количество тепла, вносимое в регенератор воздухом на сжигание кокса;

Q*_пот и Q_пот – потери тепла в окружающую среду в регенераторе и в реакторе соответственно;

Q_отв – количество тепла, отводимое из регенератора через змеевики;

Q_отв – количество тепла, уносимого из реактора продуктами;

Q_сырья – количество тепла, которое вносится в реактор с сырьем.

Количества тепла, подводимые и отводимые из реактора и регенератора большинством материальных потоков, рассчитываются по известным классическим выражениям. Для материальных потоков, компонентный состав неизвестен, количества тепла рассчитывались по различным соотношениям, приведенным в литературе.

Количество тепла, уносимого из реактора продуктами Q_прод, складывается из тепла, уносимого газообразными продуктами и жидкими продуктами, находящимися в паровой фазе. Количество тепла, уносимого жидкими продуктами, находящимися в паровой фазе, определяется по уравнению: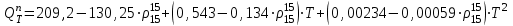

.

Тепловой эффект реакций пиролиза определяется по формуле: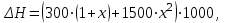



где х – степень превращения сырья.

Температура в реакторе определяется температурой в зоне смешения сырья с катализатором и температурой продуктов и катализатора на выходе из реактора следующим уравнением:

.

Температура в зоне смешения катализатора с сырьем определяется из теплового баланса в зоне смешения методом итерационного приближения: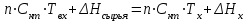

,

где n – кратность циркуляции катализатора;

Т_х – искомая температура, К;

ΔН_сырья – теплосодержание сырья при соответствующей ему температуре, с которой оно подается в реактор;

ΔН_х – теплосодержание сырья в паровой фазе после установления температуры смешения Т_х.

Температуры на выходе из реактора и температура в регенераторе находятся из тепловых балансов реактора и регенератора с использованием итерационного метода, т.е. постепенного приближения к искомому решению.

Температура на выходе из реактора определяется по уравнению



где G_кт, G_кокс, Gпрод., G_в.п. – соответственно количества катализатора, кокса, продуктов реакций пиролиза, водяного пара;

С_i – теплоемкости катализатора, кокса, продуктов реакций пиролиза, водяного пара;

ΔН_прод. – теплосодержание продуктов при искомой температуре Т_вых.

Температуру в регенераторе определяем по уравнению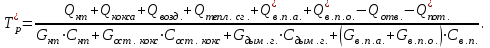



К основным входным переменным математической модели относятся температура и скорость подачи сырья, кратность циркуляции катализатора, расход и температура водяного пара, подаваемого в зону смешения, температура и расход воздуха, подаваемого в регенератор для выжига кокса.

Основными выходными переменными являются температура в аппаратах, глубина превращения сырья, состав получаемых продуктов, остаточный кокс на катализаторе и концентрация газов в продуктах горения.

Кинетические закономерности процессов пиролиза, выжига кокса описываются математической моделью разработанной на основе экспериментальных и литературных данных.

Вероятностно-статистическая кинетическая модель процессов пиролиза, по которой определяются составы получаемых продуктов на выходе из реактора, в общем виде представляет собой зависимости выхода продуктов пиролиза от параметров нормальной функции распределения: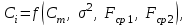



где С_m – максимально возможный выход i-го компонента;

F_ср1 и F_ср2 – средние значения фактора жесткости кривых образования или разложения;

σ² – дисперсия фактора жесткости F.

Величина степени выжига кокса в регенераторе определяется по формуле

,

где С₀ – начальная концентрация кислорода;

k₁ и k₂ – параметры, зависящие от температуры и радиуса зерен катализатора.

Математическая модель регенератора по твердой фазе как проточного реактора идеального смешения имеет вид

,

где Y – средняя степень выжига кокса;

y – степень выжига кокса на отдельном зерне;

t_к – время, необходимое для полного выжига кокса с поверхности катали-затора;

t – текущее время;

t_п=M_к/G_к – среднее время пребывания катализатора в регенераторе;

M_к – масса катализатора в регенераторе;

G_к – массовый расход подачи катализатора в регенератор.

Моделирующий алгоритм реализован следующим образом. В связи с тем, что технологические параметры работы реактора и регенератора взаимосвязаны, расчет реакторно-регенераторного блока носит итерационный характер. После ввода входных переменных задаются приближенным значением температуры катализатора на выходе из лифт-реактора (или в регенераторе) и содержанием кокса на катализаторе. Затем производится расчет регенератора. Суть расчета регенератора заключается в определении температуры в регенераторе, остаточного кокса на катализаторе и концентрации газов в продуктах горения. Зная температуру катализатора, поступающего в реактор, определяются температура в зоне смешения, температура продуктов на выходе из реактора, средняя температура в зоне реакции. В ходе расчетов определяются все составляющие материального и теплового балансов аппаратов и все выходные переменные. Выходы продуктов пиролиза при этом рассчитываются по вероятностно-статистической кинетической модели.

Вычисленная в результате расчетов температура катализатора на выходе из лифт-реактора сравнивается с исходным её значением и, если разница их превышает заранее заданную величину, принятую за критерий решённости, расчет повторяется при новом значении температуры.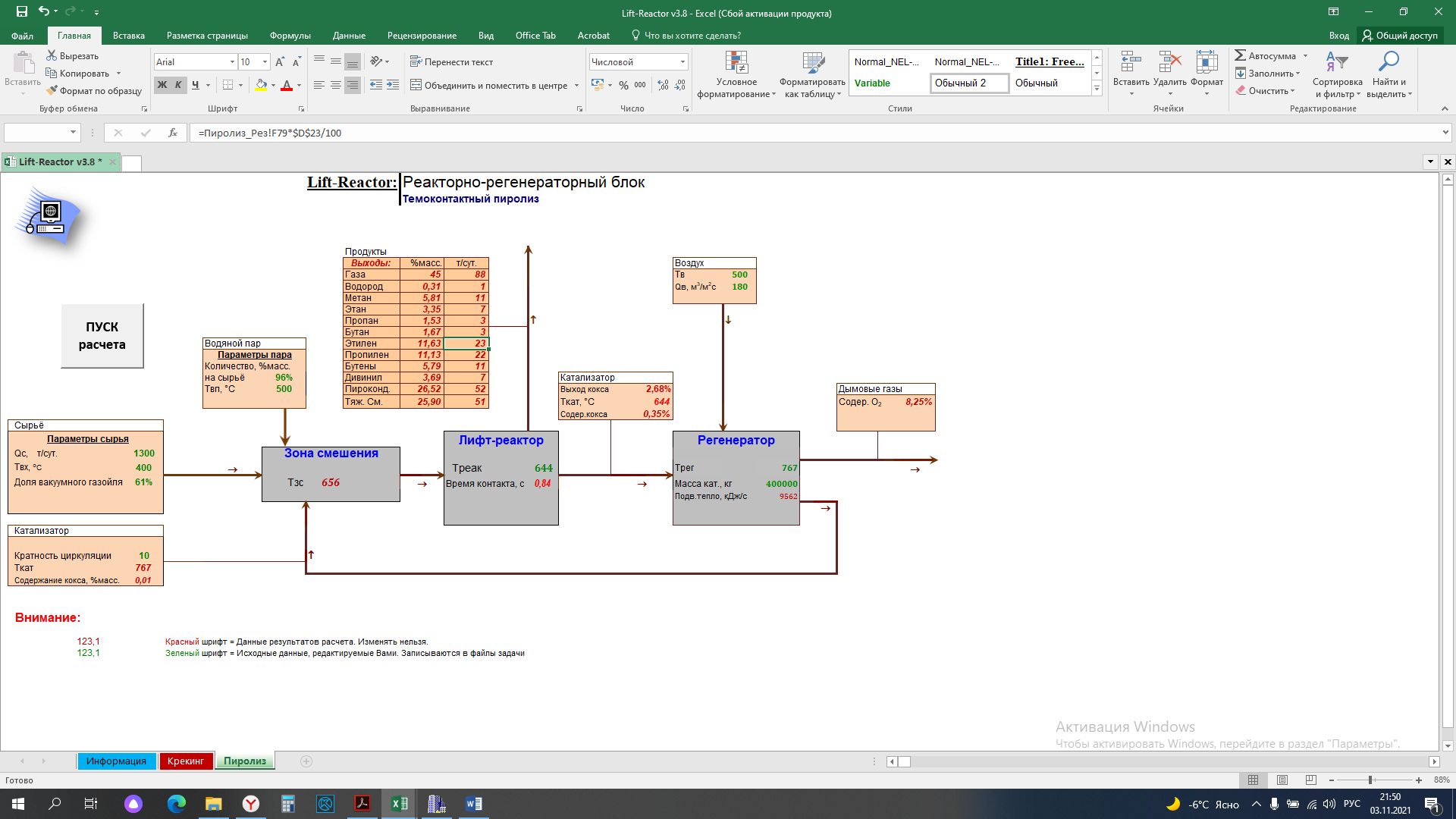




Рисунок 2 – Структурная схема реакторно-регенераторного блока процесса пиролиза

3. 
   Выполнение работы
   

1. 
   Выбор параметра оптимизации, факторов, области определения факторов и основного уровня факторов (согласно варианту задания по приложению):
   

Таблица 1 – Исходные данные

Доля вакуумного газойля в сырье, % масс.	Основной уровень		Параметр оптимизации
	х1	х2
	Температура в реакторе Тр, °С	Расход водяного пара, % масс. на сырьё	Выход продукта, т/сут
61	644	96	Этилен

2. 
   Выбираем интервалы варьирования факторов.
   
3. 
   Выбираем план. Для этого воспользуемся программой ПЛАН.ехе. После запуска программы, вводим координаты основного уровня и интервалы варьирования факторов полнофакторного эксперимента 2².
   

Рисунок 3 – Планирование эксперимента

4. 
   В программе ПЛАН.ехе составляется матрица планирования эксперимента в натуральных значениях факторов, т.е. условия проведения опытов.
   

Рисунок 4 – Матрица эксперимента

5. 
   Используя моделирующую программу Lift-Reactor.xlm согласно матрице планирования проводим первую серию компьютерных опытов. Основные технологические параметры установлены по умолчанию. Необходимо ввести значения температуры в реакторе и количество водяного пара. После нажатия на кнопку ПУСК производится итерационный расчёт реакторно-регенераторного блока. Заносим результаты опытов Y_экс в таблицу окна Матрица.
   

Таблица 2 – Результаты эксперимента

Опыт №1	Х1	Х2	Yэкс
1	654	95	64,60
2	634	95	58,47
3	654	85	65,55
4	634	85	59,54

6. 
   В программе ПЛАН.ехе переходим в окно «Шаг в направлении градиента», вводим приращение одного из факторов. При этом значение другого фактора вычисляется автоматически. Шаг должен быть меньше или равен интервалу варьирования. Если направление выбрано правильно, в окне появляется надпись «Шаг осуществляется в направлении максимума». Записываем уравнение линейной модели. Во втором столбце вычисляются значения координаты очередного основного уровня. При этих значениях проводим опыт на моделирующей программе Lift-Reactor.xlm.
   

Рисунок 5 – Шаг в направлении градиента
Уравнение линейной модели опыта №1

Y = 62,04 + 3,035 · X₁ – 0,505 · X₂

7. 
   После каждого опыта проверяем адекватность движения по градиенту фактическому поведению процесса. Легче всего это сделать, сравнивая значение оптимальности в последующем опыте со значением критерия в предыдущем опыте: если оно стало, ниже, то разрабатываем новый план, с использованием координат предыдущего опыта в качестве основного уровня. Находим новое математическое описание и т.д.
   

Таблица 3 – Результаты эксперимента

Опыт №2	Х1	Х2	Yэкс
1	684	93,336	69,54
2	664	93,336	64,78
3	684	83,336	70,17
4	664	83,336	65,58

Уравнение линейной модели опыта №2

Y = 67,517 + 2,3375 · X₁ – 0,3575 · X₂
Таблица 4 – Результаты эксперимента

Опыт №3	Х1	Х2	Yэкс
1	704	91,807	72,81
2	684	91,807	69,55
3	704	81,807	73,15
4	684	81,807	70,19

Уравнение линейной модели опыта №3

Y = 71,425 + 1,555 · X₁ – 0,245 · X₂
Таблица 5 – Результаты эксперимента

Опыт №4	Х1	Х2	Yэкс
1	724	90,231	74,58
2	704	90,231	72,90
3	724	80,231	74,72
4	704	80,231	73,24

Уравнение линейной модели опыта №4

Y = 73,86 + 0,79 · X₁ – 0,12 · X₂


Таблица 6 – Результаты эксперимента

Опыт №5	Х1	Х2	Yэкс
1	744	88,712	75,00
2	724	88,712	74,62
3	744	78,712	74,92
4	724	78,712	74,74

Уравнение линейной модели опыта №5

Y = 74,82 + 0,14 · X₁ – 0,01 · X₂
Таблица 7 – Результаты эксперимента

Опыт №6	Х1	Х2	Yэкс
1	764	87,998	74,32
2	744	87,998	74,99
3	764	77,998	74,06
4	744	77,998	74,90

Уравнение линейной модели опыта №6

Y = 74,567 – 0,3775 · X₁ + 0,0875 · X₂
Таблица 8 – Результаты эксперимента

Опыт №7	Х1	Х2	Yэкс
1	749	86,157	74,892
2	739	86,157	75,004
3	749	82,157	74,830
4	739	82,157	74,990

Уравнение линейной модели опыта №7

Y = 74,929 – 0,068 · X₁ + 0,019 · X₂


Таблица 9 – Результаты эксперимента

Опыт №8	Х1	Х2	Yэкс
1	740	85,216	75,002
2	738	85,216	74,999
3	740	84,216	74,997
4	738	84,216	74,997

Уравнение линейной модели опыта №8

Y = 74,998 + 0,00075 · X₁ + 0,0016 · X₂

8. 
   Используя EXCEL, даем геометрическую интерпретацию процесса нахождения оптимума параметра оптимизации.
   

Вывод: в данной работе мы изучили теоретические основы процесса термоконтактного пиролиза и с помощью моделирующей программы «Lift-reactor.xls» провели серии опытов и определили экстремальное значение выхода суммы олефинов 75,004 т/сут, а так же параметры, при которых данный экстремум существует Т_р = 739 °С, расход в.п. 86,157 % масс. на сырье. Используя EXCEL изобразили геометрическую интерпретацию процесса нахождения оптимума параметра оптимизации.



Рисунок 6 – Геометрическая интерпретация процесса нахождения оптимума параметра оптимизации.