для учеников 7 класа. Теоретических вопросов и задач вопросов муниципального публичного зачета по геометрии
 Скачать 246.5 Kb. Скачать 246.5 Kb.
|
|
ПЕРЕЧЕНЬ теоретических вопросов и задач вопросов муниципального публичного зачета по геометрии Вопрос № 1 1. Определение отрезка. Обозначение отрезка. Середина отрезка. Построение середины отрезка с помощью циркуля и линейки. (без доказательства) 2. Определение луча. Обозначение луча. Определение биссектрисы угла. Построение биссектрисы угла при помощи циркуля и линейки. (без доказательства) 3. Определение угла. Обозначение угла. Построение угла, равного данному. (без доказательства) 3. Определение и свойство смежных углов (формулировка). 4. Определение и свойство вертикальных углов (формулировка). 5. Определение треугольника. Стороны, вершины, углы треугольника. Периметр треугольника. 7. Определение равнобедренного треугольника. Равносторонний треугольник. Сформулировать свойства равнобедренного треугольника. 8. Определение медианы, биссектрисы и высоты треугольника. 9. Определение внешнего угла треугольника. Сформулировать свойство внешнего угла треугольника. 10. Определение остроугольного, прямоугольного, тупоугольного треугольника. Стороны прямоугольного треугольника. 11. Определение окружности. Центр, радиус, хорда, диаметр и дуга окружности. 12. Определение параллельных прямых и параллельных отрезков. Сформулировать аксиому параллельных прямых. 13. Определение расстояния от точки до прямой. Наклонная. Определение расстояния между параллельными прямыми. 14. Сформулировать признаки равенства прямоугольных треугольников. 15. Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Вопрос № 2 1. Доказать признак равенства треугольников по двум сторонам и углу между ними. 2. Доказать признак равенства треугольников по стороне и двум прилежащим углам. 3. Доказать признак равенства треугольников по трем сторонам. 4. Доказать теорему о сумме углов треугольника. 5. Доказать свойство биссектрисы равнобедренного треугольника. 6. Аксиома параллельных прямых. Доказать следствия из аксиомы параллельных. 7. Доказать свойства смежных и вертикальных углов. 8. Сформулировать признаки параллельных прямых. Доказать один по выбору обучающегося. 9. Доказать, что при пересечении двух параллельных прямых секущей накрест лежащие углы равны. 10. Доказать, что при пересечении двух параллельных прямых секущей а) соответственные углы равны, б) сумма односторонних равна 180 0. 11. Доказать свойство углов при основании равнобедренного треугольника. 12. Доказать теорему о соотношении между сторонами и углами треугольника (прямую или обратную). Следствия из теоремы. 13. Доказать, что каждая сторона треугольника меньше суммы двух других. Что такое неравенство треугольника. 14. Доказать свойство внешнего угла треугольника. 15. Доказать свойство катета прямоугольного треугольника, лежащего против угла в 300. Сформулировать обратное утверждение. Задача № 3 1. В прямоугольном треугольнике DEF катет DF равен 14 см, угол Е 300. Найдите гипотенузу DE. 2. Угол при основании равнобедренного треугольника равен 720. Найдите угол при вершине. 3.Один из углов, образованных при пересечении двух прямых, равен 700. Найти остальные три угла. 4.  Доказать равенство треугольников ADM и AFE. Доказать равенство треугольников ADM и AFE.5. Доказать равенство треугольников COD и AOD. 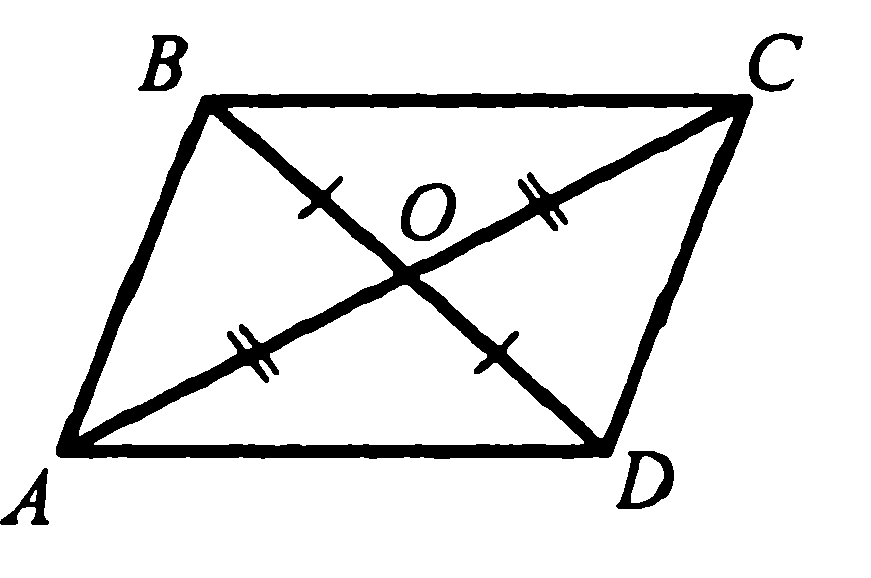 6. Один из острых углов прямоугольного треугольника 370. Найти второй острый угол. 7. В прямоугольным треугольнике ABC гипотенуза АВ равна 38 см, а угол В равен 600. Найдите катет ВС. 8. Периметр равнобедренного треугольника 19 см, а основание – 7 см. Найти боковую сторону треугольника. 9. Один из углов, образованных при пересечении двух прямых, на 500 меньше другого. Найти эти углы. 10. Внешний угол равнобедренного треугольника равен 760. Найдите углы треугольника. 11. Угол АBC и угол DCB равны 900, АС=BD. Доказать, что AD=CD.  12. Найти углы треугольника АВС.  13. Углы FDB и CBD равны, углы FBD и CDB равны. Доказать, что равны углы F и C.  14. Доказать, что прямые a и b параллельны. 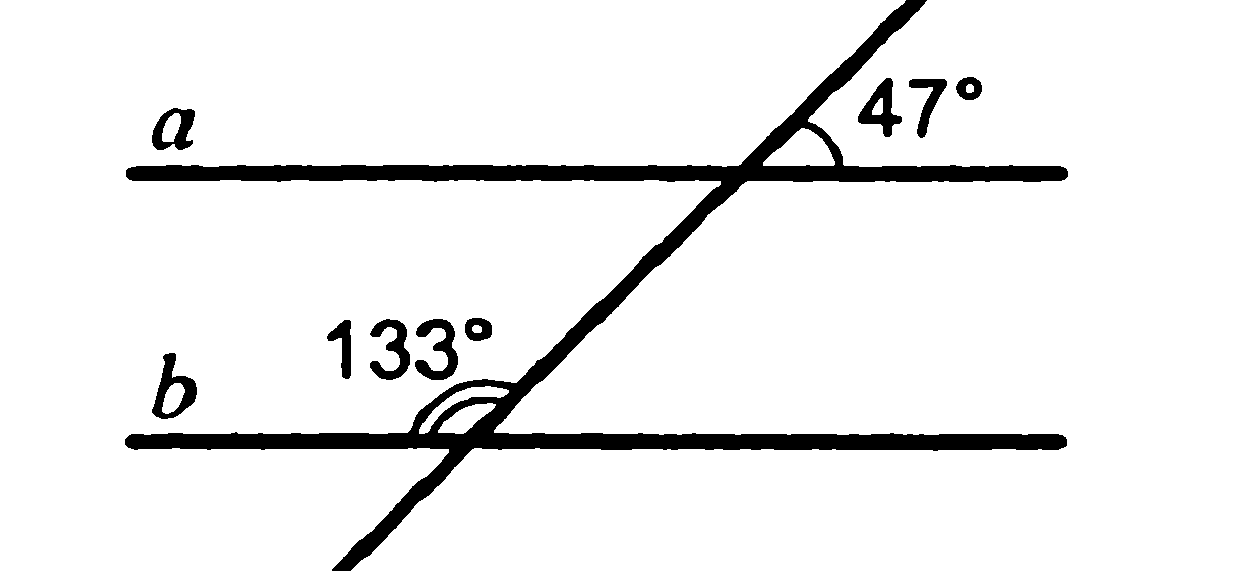 15. Луч BD проходит между сторонами угла АВС. Найдите угол DBC, если угол АВС равен 630, угол АBD равен 510. 16. Найдите угол СВА.  17. Укажите пары параллельных прямых (отрезков) и докажите их параллельность. 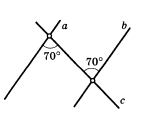 18. Найдите все неизвестные углы треугольника. 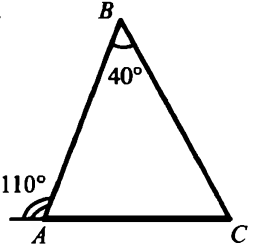 19. Дан прямоугольный треугольник АВС. Угол В равен 600.Найдите катет ВС. 20. DA – биссектриса угла BDC. Докажите равенство треугольников ABD и ACD.  21. Найдите пары равных треугольников и докажите их равенство.  22. Дана окружность с центром в точке О. Докажите, что AD=BC.  23. Дана окружность с центром в точке О. Докажите, что AВ=BC.  24. Найдите пары равных треугольников и докажите их равенство.  25. Найдите все неизвестные углы треугольника.  26. Укажите пары параллельных прямых (отрезков) и докажите их параллельность. 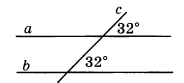 Задача № 4. 1. Точка D отрезка BC находится в 3 раза ближе к точке В, чем к точке С. Найдите BD и CD, если ВС=4,8 см. 2. Точка С отрезка АВ находится на 8,6 см ближе к точке А, чем к точке В. Найдите АС и СВ, если АВ=34 см. 3. Найдите угол, который образует биссектриса угла, равного 1780, с продолжением одной из сторон. 4. Луч с – биссектриса угла bd, а луч а – биссектриса угла bc. Найдите угол bd, если угол ad равен 960. 5. Сумма вертикальных углов в 3 раза больше смежного с ними угла. Найдите вертикальные углы. 6. Сумма вертикальных углов равна смежному с ними углу. Найдите вертикальные углы. 7. Найдите неразвернутые углы, образованные при пересечении двух прямых, если один из них в 7 раз меньше суммы трех остальных. 8. Одна из сторон равнобедренного треугольника на 3 см больше другой стороны. Найдите стороны этого треугольника, если периметр равен 24 см. Сколько решений имеет задача? 9. В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ, а в треугольнике АВМ – биссектриса МЕ. Найдите угол СМЕ. 10. В равнобедренном треугольнике АВС АВ=АС, на прямой АС вне треугольника отложены равные отрезки АD и СЕ. Докажите равенство треугольников ВСD и ВАЕ. 11. В треугольнике АВС угол А равен углу С. На сторонах АВ и СВ отложены соответственно точки M и N так ,что угол ACM равен углу NAC. Докажите, что треугольники ANB и CMB равны. 12. Дан равнобедренный треугольник АВС с основанием АС. Точки D и Е лежат соответственно на сторонах АВ и ВС, AD= СЕ. DC пересекает АЕ в точке О. Докажите, что треугольник АОС равнобедренный. 13. Отрезки АВ и СD параллельны и равны. Докажите, что треугольники АОВ и DOC равны, где О – точка пересечения отрезков AD и ВС. 14. В равнобедренном треугольнике АВС с основанием АС на стороне ВС выбрана точка Е, а на основании – точка D так, что угол С равен CDE. Докажите, что АВ и DE параллельны. 15. Угол АОВ равен 1380. Через точки А и В проведены прямые, которые параллельны сторонам данного угла и пересекаются в точке С. Найдите углы, которые образовались при пересечении этих прямых. 16. Найдите углы равнобедренного треугольника, если один из них на 270 больше другого. 17. Биссектриса равнобедренного треугольника, проведенная из вершины при основании, образует с основанием угол, равный 340. Какой угол образует медиана, проведенная к основанию, с боковой стороны? 18. В равнобедренном треугольнике АВС с основанием АС из вершин А и В проведены высоты, которые при пересечении образует угол 1000. Найдите углы треугольника. 19. В равнобедренном треугольнике АВС с основанием АС из вершин А и В проведены биссектрисы, образующие при пересечении угол 1000. Найдите углы треугольника. 20. Острый угол прямоугольного треугольника равен 380. Найдите угол между биссектрисой и высотой, проведенными из вершины прямого угла. 21. В прямоугольном треугольнике из вершины угла, равного 600, проведена биссектриса. Расстояние от основания биссектрисы до вершины другого острого угла равно 14 см. Найдите расстояние от основания биссектрисы до вершины прямого угла. 22. В окружности проведены диаметры DF и НК. Докажите, что прямые DK и FH параллельны. 23. В прямоугольным треугольнике биссектриса наименьшего угла образует с меньшим катетом углы, один из которых на 200 больше другого. Найдите острые углы данного треугольника. 24. Два угла треугольника относятся как 4:7, а внешний угол третьего угла равен 1210. Найдите углы треугольника. 25. Биссектриса угла при основании равнобедренного треугольника равна основанию треугольника. Найдите его углы. 26. В прямоугольном треугольнике АВС (угол С=900). На катете АС выбрана точка D так, что CD в 2 раза меньше BD, BD=AD. Найдите биссектрису угла В, если CD меньше AD на 25 см. |
