производная. Теоретический материал для самостоятельного изучения

• Название: Теоретический материал для самостоятельного изучения
• Дата: 16.03.2022
• Размер: 55.28 Kb.
• Имя файла: производная.docx
• Тип: Документы; #400235

Теоретический материал для самостоятельного изучения

Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.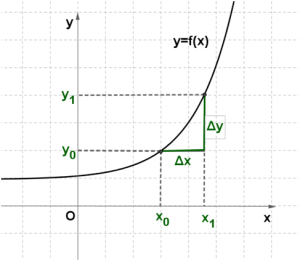



Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Итак, x₁-x₀=Δx, значит, x₁=x₀+Δx.

f(x₁)-f(x₀)=Δy, значит, 

Δy=f(x₀+Δx)-f(x₀). (1)

Нельзя истолковывать термин "приращение" как "прирост".

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найдем приращение Δx и Δf в точке x_0, если f(x)= x², x₀=2 и х=1,9

Решение:

Δx= x₁−x₀=1,9-2=-0,1

Δf= f(1,9) –f(2)=1,9²-2²=-0,39

Ответ: Δx=-0,1; Δf =-0,39

Пример 2.

Найдем приращение Δx и Δf в точке x_0, если f(x)= x², x₀=2 и х=2,1

Решение:

Δx= x₁−x₀=2,1-2=0,1

Δf= f(1,9) –f(2)=2,1²-2²=0,41

Ответ: Δx=0,1; Δf =0,41

Пример 3.

Найдем приращение Δf функции   в точке x₀,если приращение аргумента равно x₀.

Решение:

по формуле (1) находим:

.

Ответ:  .

С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀; t₀+∆t]. Если точка движется по прямой и известна ее координата x(t), то



Эта формула верна и для ∆t<0 (для промежутка [t₀+∆t; t₀]).

Аналогично выражение   называют средней скорость изменения функции на промежутке с концами х₀ и х₀+∆х.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.



Обозначение: y’ или f’(x)

Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

Схема вычисления производной функции

1. 
   Найти приращение функции на отрезке [x; x+Δx]:
   

∆y=y(x+∆x)-y(x)

1. 
   Разделить приращение функции на приращение аргумента:
   

1. 
   Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
   

Пример 4.

Вычислить производную функции y=x²

Решение: Используем схему вычисления производной по действиям:

1. 
   ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
   
2. 
   
   
3. 
   
   

Ответ: y’=2x.

Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).

Таким образом, скорость – есть производная от пути по времени.

Пример 5.

Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.

Решение:

найдем ∆t= 1-0,8=0,2

S(0,8)= 1-2·0,8= -0,6=S(t)

S(1)= 1-2·1= -1=S(t+∆t)

.

Ответ:  _.

Необходимое и достаточное условие дифференцируемости

Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.