Лекция. Теоретическое обоснование

• Название: Теоретическое обоснование
• Дата: 12.03.2022
• Размер: 456 Kb.
• Имя файла: Лекция.doc
• Тип: Документы; #392868

Комплексные оценки защищенности автоматизированных систем

Теоретическое обоснование

Уязвимость информации есть событие, возникающее как результат такого стечения обстоятельств, когда в силу каких-то причин используе­мые в АСОД средства защиты не в состоянии оказать достаточного противодействия проявлению дестабилизирующих факторов и нежелательного их воздействия на защищаемую информацию. Модель уязвимости информации в АСОД в самом общем виде представлена на рисунке 3.1. Дан­ная модель детализируется при изучении конкретных видов уязвимости информации: нарушения физической или логической целостности, не­санкционированной модификации, несанкционированного получения, несанкционированного размножения.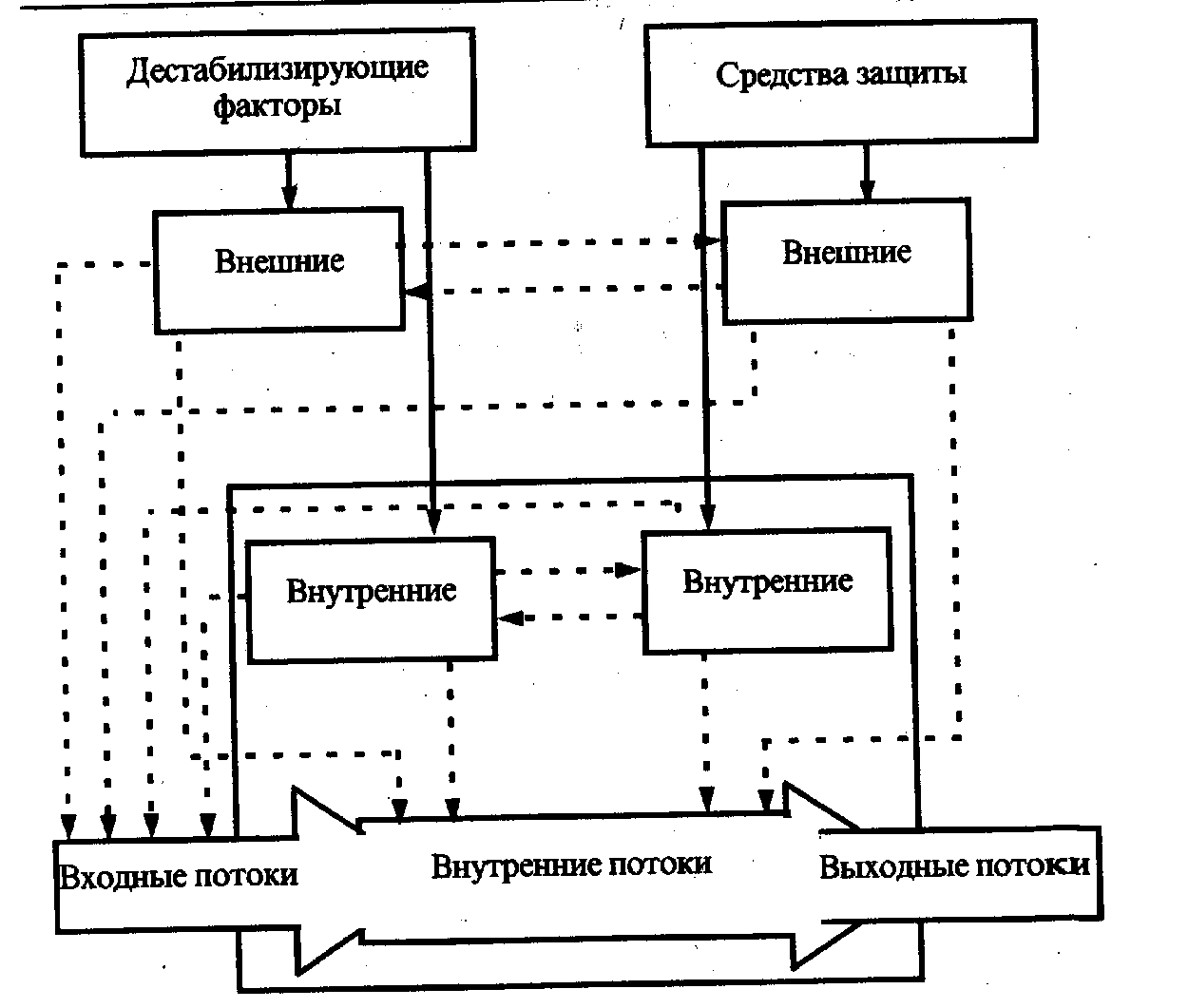


Рисунок 3.1 – Общая модель воздействия на информацию
При детализации общей модели основное внимание акцентируется на том, что подавляющее большинство нарушений физической целостности информации имеет место в процессе ее обработки на различных участках технологических маршрутов. При этом целостность информации в каждом объекте АСОД существенно зависит не только от процессов, происходящих на объекте, но и от целостности информации, поступающей на его вход. Основную опасность представляют случайные дестабилизирующие факторы (отказы, сбои и ошибки компонентов АСОД), которые потенциально могут проявиться в любое время, и в этом отношении можно говорить о регулярном потоке этих факторов. Из сти­хийных бедствий наибольшую опасность представляют пожары, опас­ность которых в большей или меньшей степени также является постоян­ной. Опасность побочных явлений практически может быть сведена к ну­лю путем надлежащего выбора места для помещений АСОД и их обору­дования. Что касается злоумышленных действий, то они связаны, глав­ным образом, с несанкционированным доступом к ресурсам АСОД. При этом наибольшую опасность представляет занесение вирусов.

В соответствии с изложенным общая модель процесса нарушения физической целостности информации на объекте АСОД может быть представлена так, как показано на рисунке 3.2.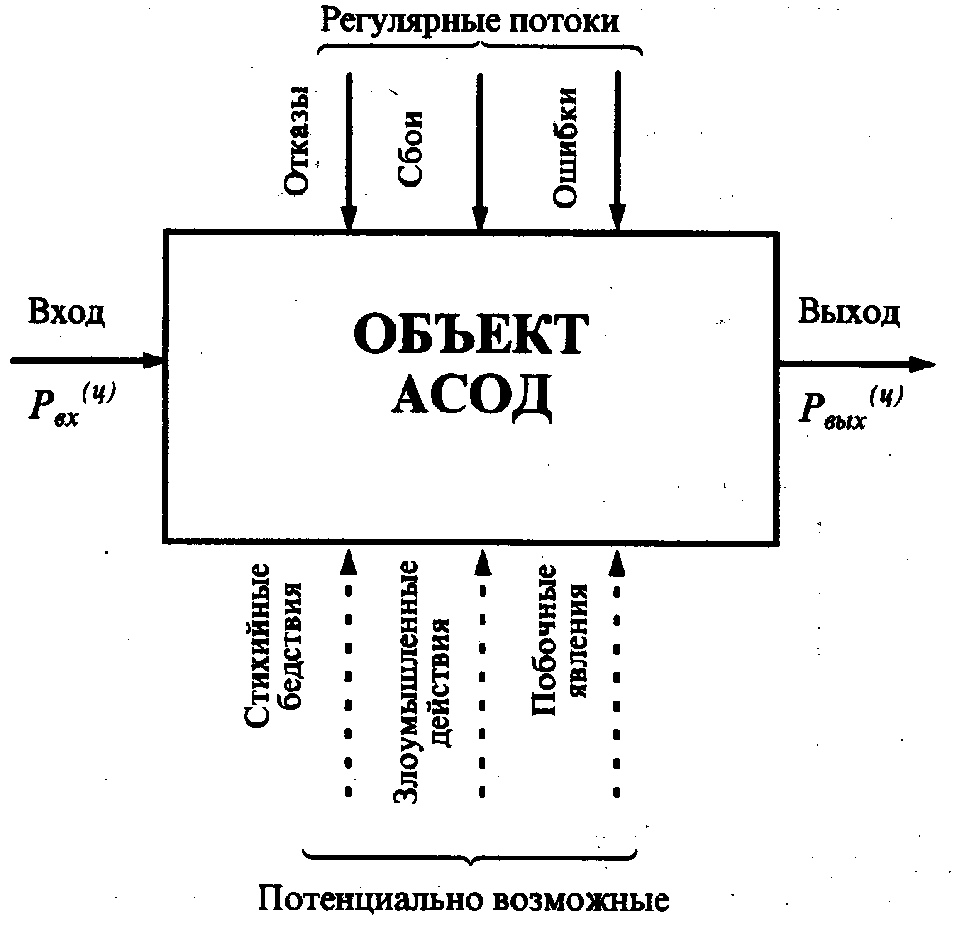


Рисунок 3.2 – Общая модель процесса нарушения физической целостности информации

С точки зрения несанкционированного получения информации принципиально важным является то обстоятельство, что в современных АСОД оно возможно не только путем непосредственного доступа к базам данных, но и многими путями, не требующими такого доступа. При этом основную опасность представляют злоумышленные действия людей. Воздействие случайных факторов само по себе не ведет к несанкционированному получению информации, оно лишь способствует появлению, КНПИ, которыми может воспользоваться злоумышленник. Структури­рованная схема потенциально возможных злоумышленных действий в современных АСОД для самого общего случая представлена на рисунке 3.3.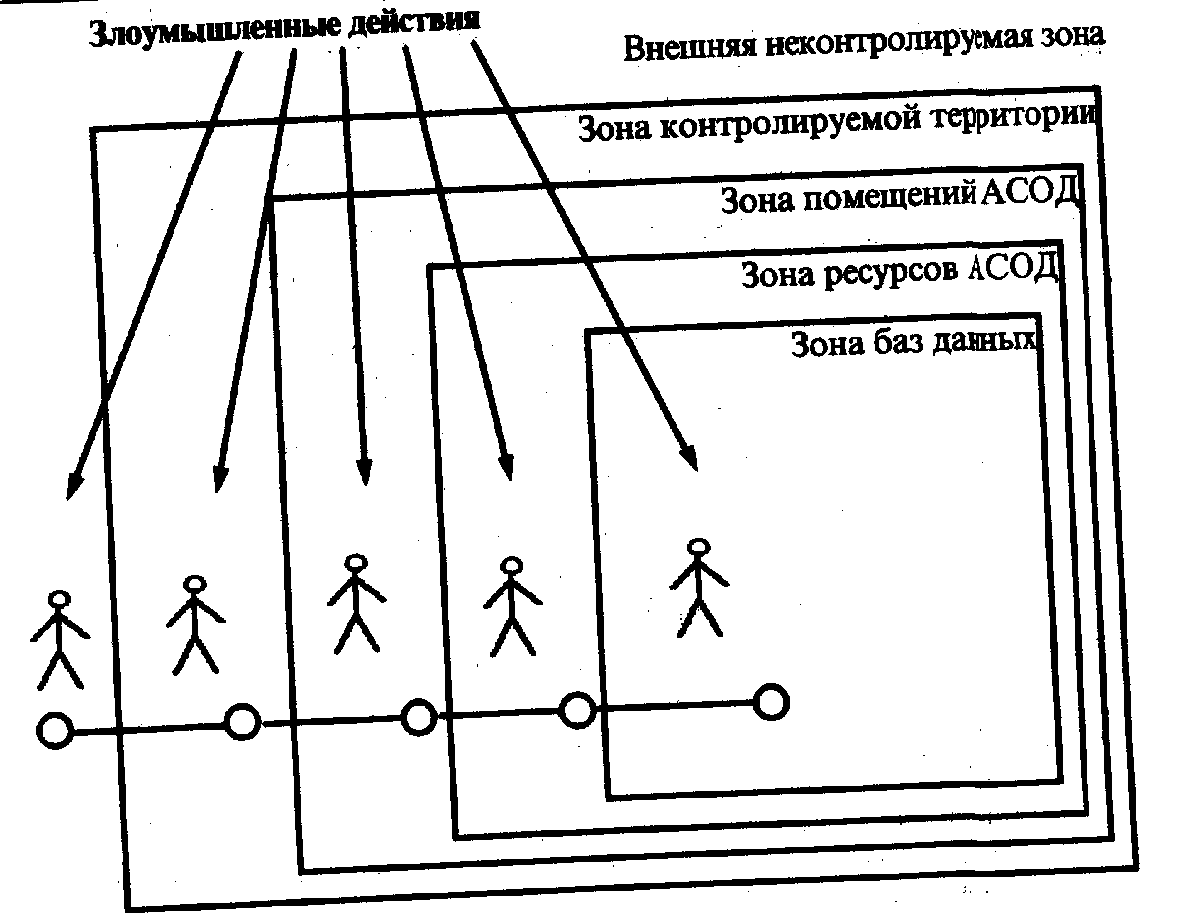

Рисунок 3.3 – Структурированная схема потенциально возможных злоумышленных действий в АСОД

Выделенные на рисунке зоны определяются следующим образом:

1) внешняя неконтролируемая зона – территория вокруг АСОД, на которой персоналом и средствами АСОД не применяются никакие сред­ства и не осуществляются никакие мероприятия для защиты информации;

2) зона контролируемой территории – территория вокруг помеще­ний АСОД, которая непрерывно контролируется персоналом или средствами АСОД;

3) зона помещений АСОД – внутреннее пространство тех помеще­ний, в которых расположены средства системы;

4) зона ресурсов АСОД – та часть помещений, откуда возможен непосредственный доступ к ресурсам системы;

5) зона баз данных – та часть ресурсов системы, с которых возможен непосредственный доступ к защищаемым данным.

Злоумышленные действия с целью несанкционированного получе­ния информации в общем случае возможны в каждой из перечисленных зон. При этом для несанкционированного получения информации необ­ходимо одновременное наступление следующих событий: нарушитель должен получить доступ в соответствующую зону; во время нахождения нарушителя в зоне в ней должен проявиться (иметь место) соответствующий КНПИ; соответствующий КНПИ должен быть доступен на­рушителю соответствующей категории; в КНПИ в момент доступа к нему нарушителя должна находится защищенная информация.

Рассмотрим далее трансформацию общей модели уязвимости с точ­ки зрения несанкционированного размножения информации. Принципи­альными особенностями этого процесса являются:

1) любое несанкционированное размножение есть злоумышленное действие;

2) несанкционированное размножение может осуществляться в организациях-разработчиках компонентов АСОД, непосредственно в АСОД и сторонних организациях, причем последние могут получать но­ситель, с которого делается попытка снять копию как законным, так и незаконным путем.

Попытки несанкционированного размножения информации у разработчика и в АСОД есть один из видов злоумышленных действий с целью несанкционированного ее получения и поэтому имитируются приведенной выше (см. рисунок 3.3) моделью. Если же носитель с защищаемой информацией каким-либо путем (законным или незаконным) попал в стороннюю организацию, то для его несанкционированного копирования могут использоваться любые средства и методы, включая и такие, кото­рые носят характер научных исследований и опытно-конструкторских разработок. Тогда модель процесса размножения в самом общем виде может быть представлена так, как показано на рисунок 3.4.

Для определения значений показателей уязвимости информации должны быть разработаны методы, соответствующие природе этих показателей и учитывающие все факторы, влияющие на их значение. На осно­ве этих методов должны быть разработаны модели, позволяющие рассчитывать значения любой совокупности необходимых показателей и при любых вариантах архитектурного построения АСОД, технологии и усло­вий ее функционирования.

Ниже рассматриваются подходы к разработке названных методов и моделей.

В процессе развития теории и практики защиты информации сформировалось три методологических подхода к оценке уязвимости информации: эмпирический, теоретический и теоретико-эмпирический.

Сущность эмпирического подхода заключается в том, что на основе длительного сбора и обработки данных о реальных проявлениях угроз информации и о размерах того ущерба, который при этом имел место, чисто эмпирическим путем устанавливаются зависимости между потен­циально возможным ущербом и коэффициентами, характеризующими частоту проявления соответствующей угрозы и значения имевшего при ее проявлении размера ущерба.

Наиболее характерным примером моделей рассматриваемой разновидности являются модели, разработанные специалистами американской фирмы IBM. Рассмотрим развиваемые в этих моделях подходы.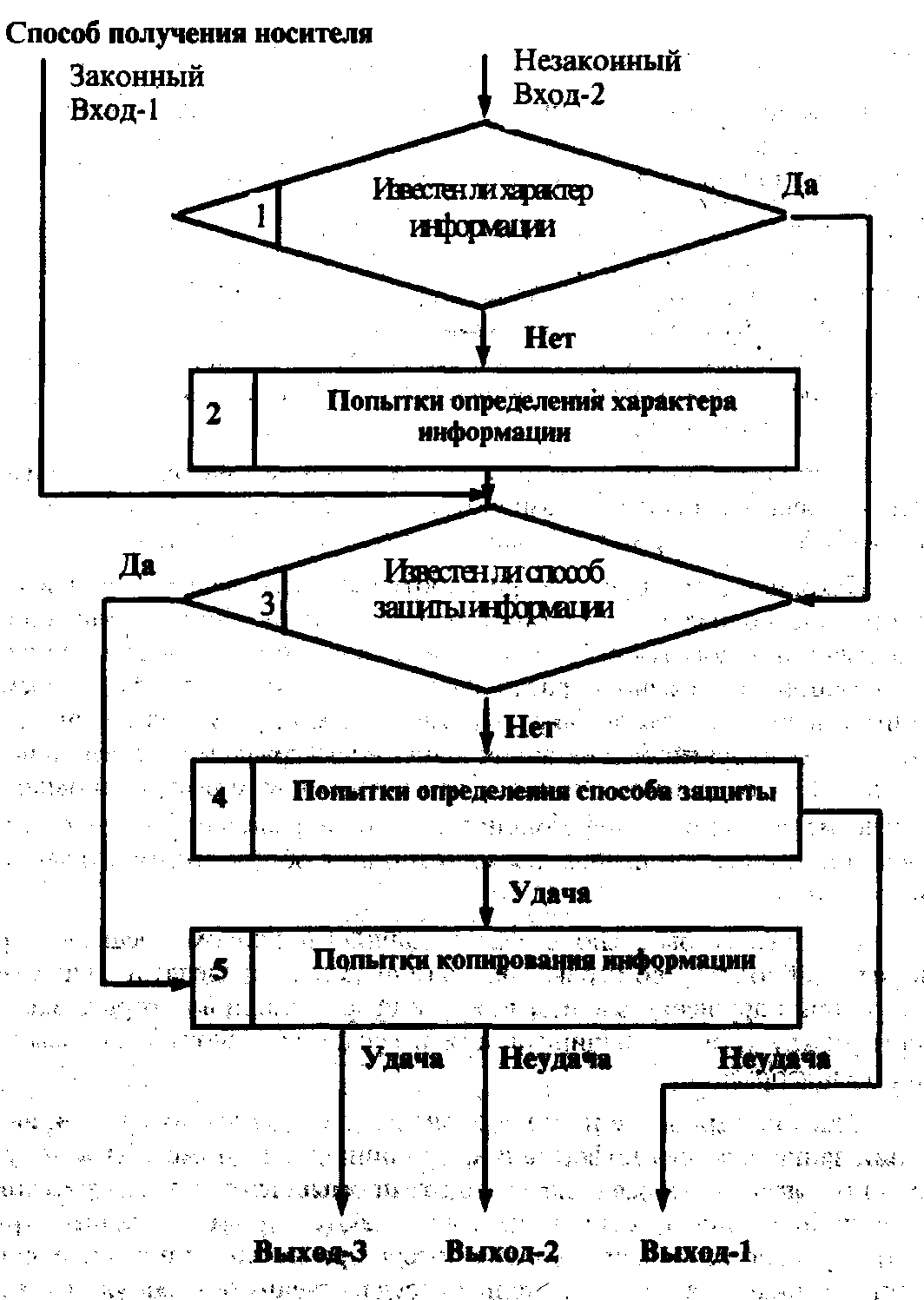


Рисунок 3.4 – Общая модель процесса несанкционированного копирования информации

Исходной посылкой при разработке моделей является почти оче­видное предположение: с одной стороны, при нарушении защищенности информации наносится некоторый ущерб, с другой, обеспечение защиты информации сопряжено с расходованием средств. Полная ожидаемая стоимость защиты может быть выражена суммой расходов на защиту и потерь от ее нарушения. Указанная зависимость графически представлена на рисунке 3.5. Совершенно очевидно, что оптимальным решением было бы выделение на защиту информации средств в размере С_орt, поскольку именно при этом обеспечивается минимизация общей стоимости защиты информации.

Для того чтобы воспользоваться данным подходом к решению проблемы, необходимо, во-первых, знать (или уметь определять) ожидаемые потери при нарушении защищенности информации, а во-вторых, зависимость между уровнем защищенности и средствами, затрачиваемыми на защиту информации.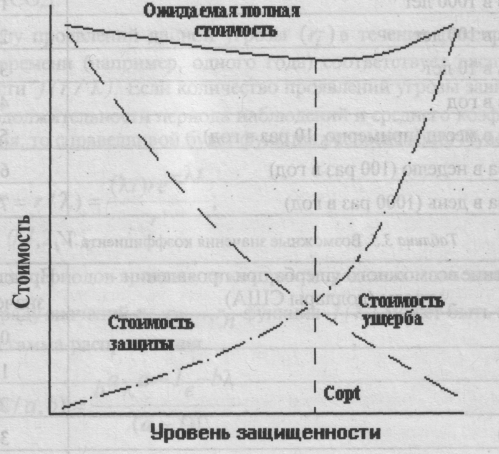


Рисунок 3.5 – Стоимостные зависимости защиты информации
Решение первого вопроса, т.е. оценки ожидаемых потерь при нарушении защищенности информации, принципиально может быть получено лишь тогда, когда речь идет о защите промышленной, коммерческой и им подобной тайны, хотя и здесь встречаются весьма серьезные труд­ности. Что касается оценки уровня потерь при нарушении статуса защи­щенности информации, содержащей государственную, военную и им по­добную тайну, то здесь до настоящего времени строгие подходы к их по­лучению не найдены. Данное обстоятельство существенно сужает возможную область использования моделей, основанных на рассматри­ваемых подходах.

Для определения уровня затрат, обеспечивающих требуемый уро­вень защищенности информации, необходимо по крайней мере знать, во-первых, полный перечень угроз информации, во-вторых, потенциаль­ную опасность для информации каждой из угроз и, в-третьих, размеры затрат, необходимых для нейтрализации каждой из угроз.

Поскольку оптимальное решение вопроса о целесообразном уровне затрат на защиту (см. рисунок 3.5) состоит в том, что этот уровень должен быть равным уровню ожидаемых потерь при нарушении защищённости, достаточно определить только уровень потерь. Специалистами фирмы IBM предложена следующая эмпирическая зависимость ожидаемых по­терь от i-ой угрозы информации:
(3.1)

где Si - коэффициент, характеризующий возможную частоту возникнове­ния соответствующей угрозы;

V_i- коэффициент, характеризующий зна­чение возможного ущерба при ее возникновении. Предложенные специа­листами значения коэффициентов приведены в таблицах 3.1 и 3.2.

Таблица 3.1 – Значение коэффициента Si

Ожидаемая (возможная) частота появления угрозы	Предполагаемое значение Si
Почти никогда	0
1 раз в 1000 лет	1
1 раз в 100 лет	2
1 раз в 10 лет	3
1 раз в год	4
1 раз в месяц (примерно, 10 раз в год)	5
2 раза в неделю (100 раз в год)	6
3 раза в день (1000 раз в год)	7

Таблица 3.2 – Возможные значения коэффициента V_i

Значения возможного ущерба при проявлении угрозы (доллары США)	Предполагаемое значение Vi
1	0
10	1
100	2
1000	3
10 000	4
100 000	5
1 000 000	6
10 000 000	7

Суммарная стоимость потерь определяется формулой

(3.2)

Условность и приближенность рассмотренного подхода является очевидной, и это серьезно подрывает доверие к рассматриваемой модели. Попытки повысить адекватность модели приводят к достаточно слож­ным аналитическим выкладкам, основанным на методах теории вероят­ностей и теории принятия решений. Для иллюстрации приведем так на­зываемую динамическую модель оценки потенциальных угроз.

Пусть , есть средний коэффициент возможного появления угрозы рассматриваемого типа. Для общего случая этот коэффициент рассматривается как случайная переменная , с распределением вероятностей f . Функция распределения должна определяться на основе обработ­ки данных о фактах проявления угроз в процессе реального функциони­рования АСОД.

Числу проявлений данной угрозы в течение фиксированного периода времени (например, одного года) соответствует распределение вероятности . Если количество проявлений угрозы зависит толь­ко от продолжительности периода наблюдений и среднего коэффициента проявления, то справедливой будет функция распределения Пуассона:

; (3.3)

r = 0,1,2,…,

где t - число периодов времени, за которые определены значения r.

По ряду значений r₁,r₂,…,r_n функция может быть выражена функцией гамма-распределения

(3.4)

где а и b- параметры распределения, определяемые по рекуррентным зависимостям:
(3.5)
где - число проявлений рассматриваемой угрозы в периоды наблюдения .

Безусловное распределение вероятностей числа проявления угроз за период времени tопределяется выражением

(3.6)

Результирующее распределение выражается в следующем виде:

(3.7)

Эффективность защиты в заданное число периодов функциониро­вания системы характеризуется параметрами а и b. Ожидаемое количе­ство проявления угроз в последние tпериодов характеризуется математи­ческим ожиданием

(3.8)

и дисперсией

(3.9)

Так определяются показатели возможностей проявления угроз. Подходы к оценке стоимости проявления угроз состоят в следующем. Первоначально рассматриваются средние стоимости проявления угроз, поэтому принимается нормальная функция распределения с параметра­ми т и V:

(3.10)

где и нормальное и гамма-распределения вероятностей; и - параметры гамма-распределения.

Если в последующиеtпериодов времени происходит r проявлений рассматриваемой угрозы, которые приводят к ущербу в размере соответственно , то п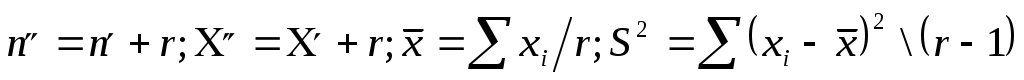араметры распределения вероятностей ожидаемых потерь корректируются следующим образом:

;
; (3.11)
где

Прогнозируемое распределение для ущерба от возможного прояв­ления рассматриваемой угрозы формируется путем выделения неопреде­ленных параметров т и Vиз функции распределения вероятностей для стоимости проявления угрозы данного типа. В соответствии с этим полу­чается

, (3.12)

- член семейства распределения Стьюдента.

Ожидаемое изменение значения хопределяются параметрами: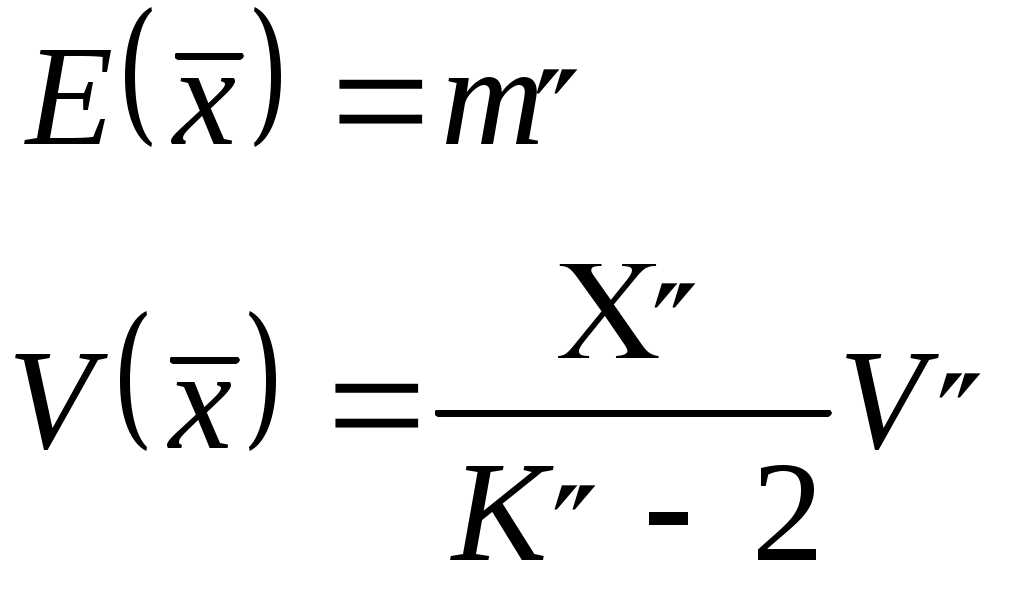
(3.13)

Поскольку возможное число проявлений i -ой угрозы данного типа за данный период времени является случайной переменной (r_i) и стои­мость каждого проявления этой угрозы - также случайной переменной (x_ij),где j=1, 2,...,r, то ожидаемая полная стоимость угроз за t перио­дов времени ( ) определяется по формуле

(3.14)

Ожидаемая стоимость проявления угрозы одного (i-го) типа ( ) определяется по формуле

(3.15)

Поскольку стоимости проявления угроз являются случайными величинами, для полной их оценки необходимо найти функции распределения их вероятностей.

Таким образом, если бы удалось собрать достаточное количество фактических данных о проявлениях угроз и их последствиях, то рассмотренную модель можно было бы использовать для решения достаточно широкого круга задач зашиты информации, причем, нетрудно видеть, что модель позволяет не только находить нужные решения, но и оцени­вать их точность. По России такая статистика в настоящее время практи­чески отсутствует. В США же, например, сбору и обработке указанных данных большое внимание уделяет целый ряд учреждений (Стенфордский исследовательский институт и др.). В результате уже получены достаточ­но представительные данные по целому ряду угроз, которые могут быть положены в основу ориентировочных расчетов и для других стран.

Учитывая важность данного вопроса, представляется настоятельно актуальной организация непрерывного и регулярного сбора и обработки данных о проявлениях угроз, охватывающего возможно большее число АСОД.

Рассмотренная выше модель допускает также игровую интерпрета­цию, т.е. может быть приведена к постановке в терминах теории игр. Предположим, что злоумышленник затрачивает х средств с целью преодоления механизма защиты, на создание которого израсходовано у средств. Естественно, ожидаемое количество информации, получаемое злоумышленником, есть некоторая функции I(x,y). Если далее f(n) – есть ценность для злоумышленника n единиц информации, a g(n) суммарные затраты на создание и сбережение этого же числа единиц информации, то чистая прибыль злоумышленника

(3.16)

а потери

(3.17)

В соответствии с известными правилами теории игр оптимальные стратегии обеих сторон могут быть определены из условий: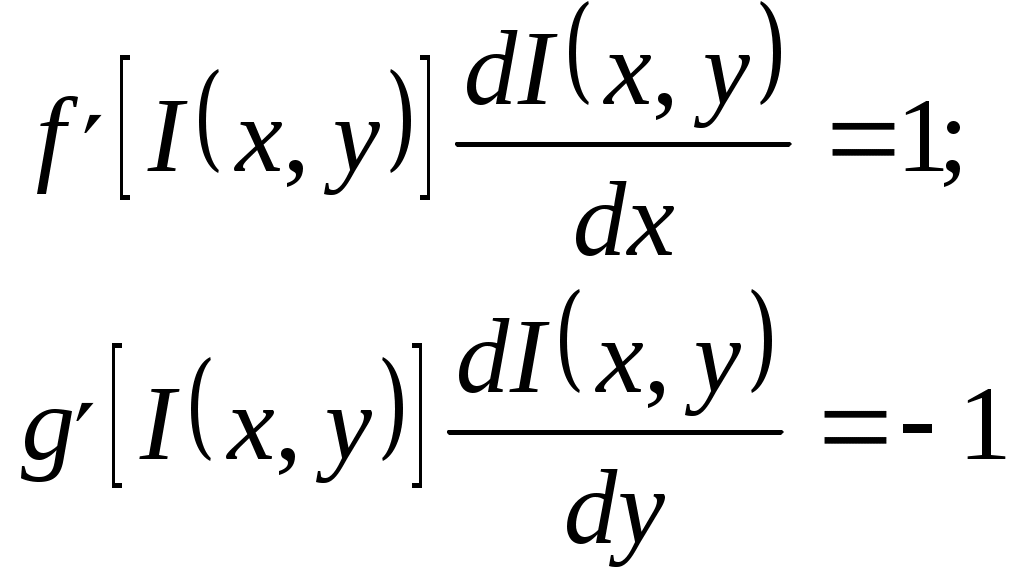

(3.18)

В теоретическом отношении эта модель является достаточно стро­гой, однако для практического использования необходимо определить стоимость информации, а также построить функции I, f и g для общего случая, что в настоящее время пока является нерешенной проблемой.

Естественным продолжением моделей оценки угроз АСОД являют­ся модели нейтрализации этих угроз, т.е. модели защиты. Наиболее об­щей моделью защиты является модель так называемой системы с полным перекрытием.

При построении данной модели в качестве исходной взята естественная посылка, состоящая в том, что в механизме защиты должно содержаться, по крайней мере одно средство для перекрытия любого потенциально возможного канала утечки информации. Методика формального описания такой системы заключается в следующем:

1) составляется полный перечень объектов О системы, подлежащих защите;

2) составляется полный перечень потенциально возможных угроз Т информации, т.е. возможных вариантов злоумышленных действий;

3) составленные таким образом множества объединяются в двудольный граф с соблюдением условия: ребро существует только тогда, когда угроза t_iявляется реальной для объекта о_j;

4) для каждого ребра в графе определяется количественная мера соответствующей угрозы для соответствующего объекта;

5) формируется множество М средств зашиты информации в вычислительной системе;

6) определяется количественная мера возможности противодействия каждого средства защиты каждой из угроз. Если возможность противодействия превышает уровень угрозы, то соответствующее ребро графа исключается.

Очевидно, если множество M такое, что устраняются все ребра гра­фа, то такая система является системой с полным перекрытием.

Одной из разновидностей теоретически строгих моделей являются модели систем разграничения доступа к ресурсам АСОД.

В самом общем виде существо этих моделей может быть представлено следующим образом; АСОД является системой множественного до­ступа, т.е. к одним и тем же ее ресурсам (техническим средствам, про­граммам, массивам данных) имеет законное право обращаться некоторое число пользователей (абонентов). Если какие-либо из указанных ресурсов объявляются защищаемыми, то доступ к ним должен осуществляться лишь при предъявлении соответствующих полномочий. Система разгра­ничения доступа и должна стать тем механизмом, который регулирует такой доступ. Требования к этому механизму на содержательном уровне состоят в том, чтобы, с одной стороны, не должен быть разрешен доступ пользователям (или их процессам), не имеющим на это полномочий, а с другой - не должно быть отказано в доступе пользователям (или их процессам), имеющим соответствующие полномочия.

Рассмотрим примеры моделей названных механизмов, т.е. систем разграничения доступа. Одной из первых таких моделей было формаль­ное описание механизма системы АДЕПТ-50. Основными структурными элементами модели являются объекты следующих типов: пользователь u,заданиеj, терминал tи файлf. Объект каждого типа полностью описы­вается заданием четырех характеристик:

А – уровень компетенции, выраженный наибольшим грифом секретности данных (для данного объекта);

С – категория доступа, выражен­ная набором рубрик, к данным по которым разрешен доступ для объекта;

F – полномочия, выраженные списком пользователей, имеющих доступ к объекту;

M – режим, выраженный перечнем процедур, разрешенных для соответствующего объекта.

На основе такого формального описания системы можно сформулировать систему формальных правил регулирования доступа:

1) пользователь и получает доступ к заданию jтогда и только тог­да, когда , где U - множество всех пользователей, зарегистрирован­ных в системе;

2) пользователь и получает доступ к терминалу tтогда и только тогда, когда ;

3) пользователь и получает доступ к файлу f тогда и только тогда, когда: ;

4) с терминала tможет быть осуществлен доступ к файлу f тогда и только тогда, когда: .

Нетрудно видеть, что набор подобных правил может и расширять­ся, и модифицироваться. На основе же совокупности правил легко по­строить алгоритм управления доступом к данным.

К подобному типу относится разработанная несколько позже так называемая пятимерная модель безопасности. Для формального описания процесса доступа к данным в условиях защиты введено пять следующих множеств: U - список зарегистрированных пользователей; R - набор имеющихся в системе ресурсов; S - множество возможных состояний ресурсов; Е- набор операций над ресурсами; А - перечень возможных полномочий пользователей.

Вводится понятие области безопасности как декартового произведения перечисленных множеств.

D = UARSE.

В области безопасности могут быть выделены подобласти, соответствующие отдельным пользователям, группам пользователей, отдельным ресурсам и т.п.

Любой запрос на доступ может быть описан четырехмерным кор­тежем

, где

Запрос получает право на доступ только в том случае, если он по­падает в соответствующую подобласть области безопасности.

Описанная структуризация позволяет построить алгоритмическую процедуру управления доступом. Обобщением моделей рассмотренного выше типа является модель, в которой сформулирована и строго решена задача разграничения доступа.

Постановка задачи сформулирована следующим образец. Дана си­стема (А, В, g), в которой:

- конечный набор субъектов (активных элементов) системы;

- конеч­ный набор объектов (пассивных элементов) системы; a_i - код доступа субъекта i;

bj - код доступа объекта j (i, j - некоторые двоичные п-разрядные числа);

- механизм доступа, причем

если , то субъекту i разрешается доступ к объекту У;

если , тo указанный доступ не разрешается.

Задача заключается в том, чтобы при заданных наборах субъектов и объектов с их ограничениями в иерархических структурах и заданном механизме доступа выбрать такое значение разрядности кода доступа п и определить такое распределение значений кодов доступа субъектов и объектов, чтобы обеспечивались все разрешенные доступы и минимизи­ровалось число неразрешенных доступов.

Механизмом доступа может быть любая функция из семейства бу­левых функций

(3.19)

удовлетворяющая условию: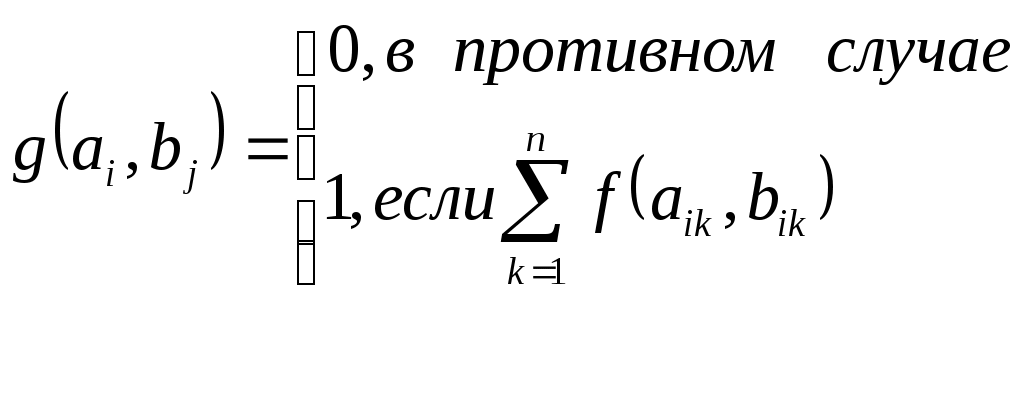

(3.20)

Здесь: произвольная булева функция двух бит; a_ik- зна­чение k-гoбита в коде доступа j-го субъекта; bj_k - значение k-гoбита в коде доступа j-го объекта; т - порог доступа, причем 0 < т < п.

С целью получения выражений для количественных оценок введены следующие определения:

1) пусть Х_ijи Y_ijесть такие булевы переменные, что Х_ij = 1 (Y_ij = 1) означает, что A_i, имеет разрешенный (неразрешенный) доступ к В_jиначе .При этом для всех и всех j , где /Z / означает кардинальное число множества Z;

2) пусть X_jбудет числом субъектов 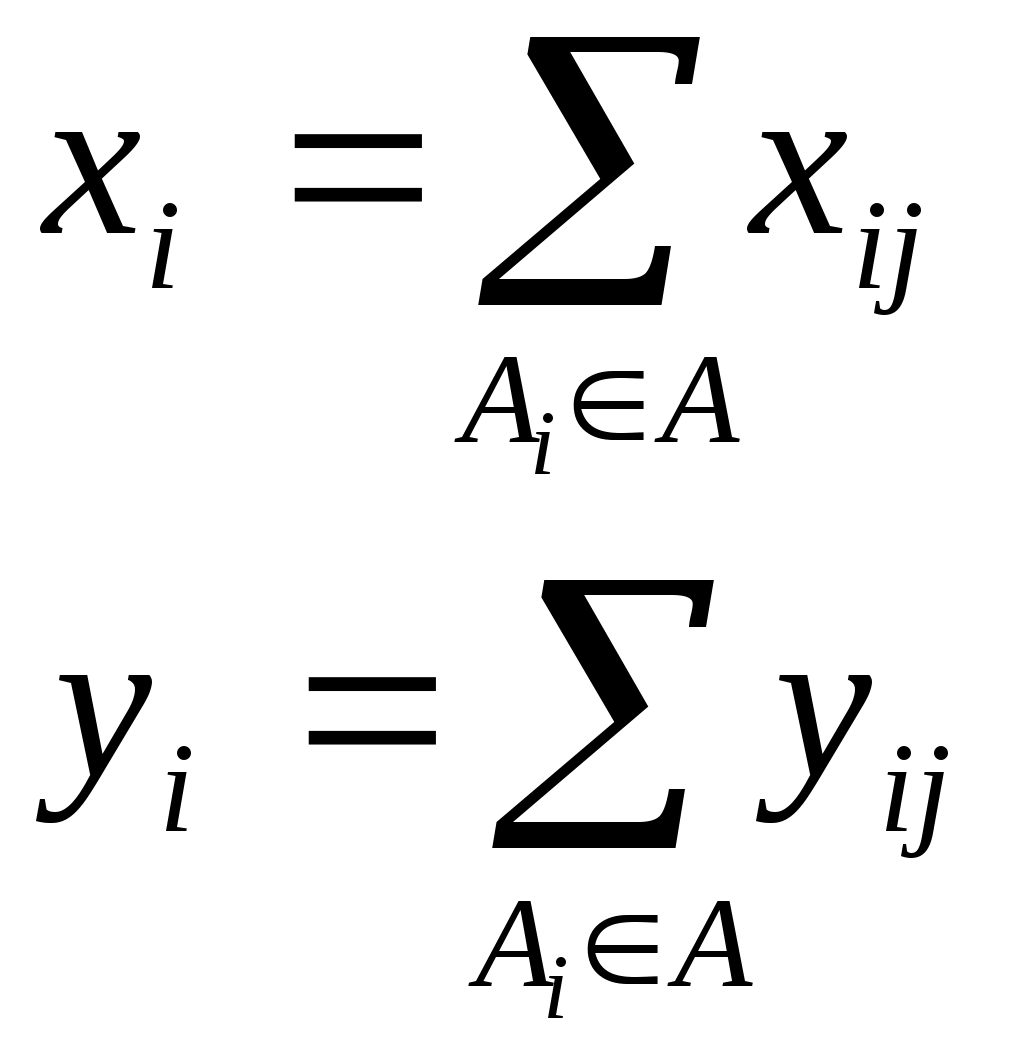имеющих разрешенный доступ к B_j,y_j - число субъектов, не имеющих такого доступа, причем:

(3.21)

3) пусть х(у) есть среднее (по В) число субъектов, имеющих разрешенный (неразрешенный) доступ к любому 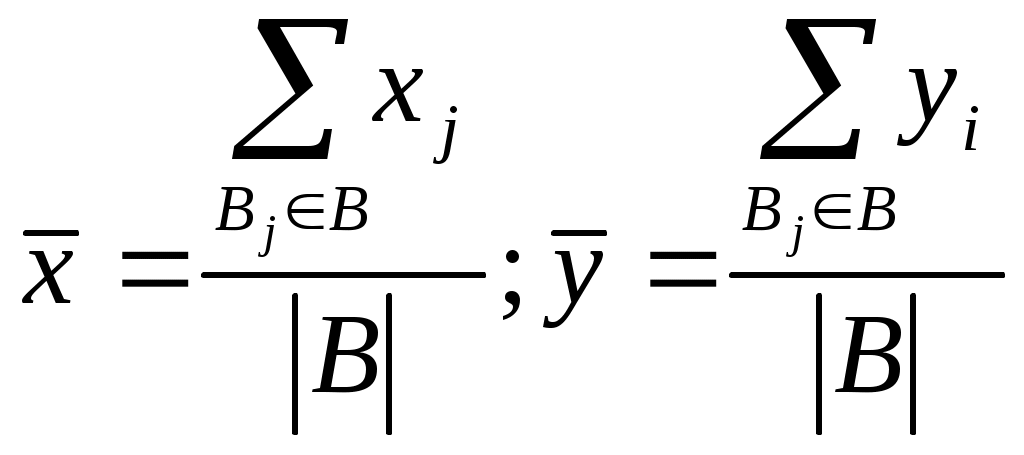,т.е.

(3.22)

4) пусть х(у) будет минимальным (по В) числом субъектов, имею­щих разрешенный (неразрешенный) доступ к любому 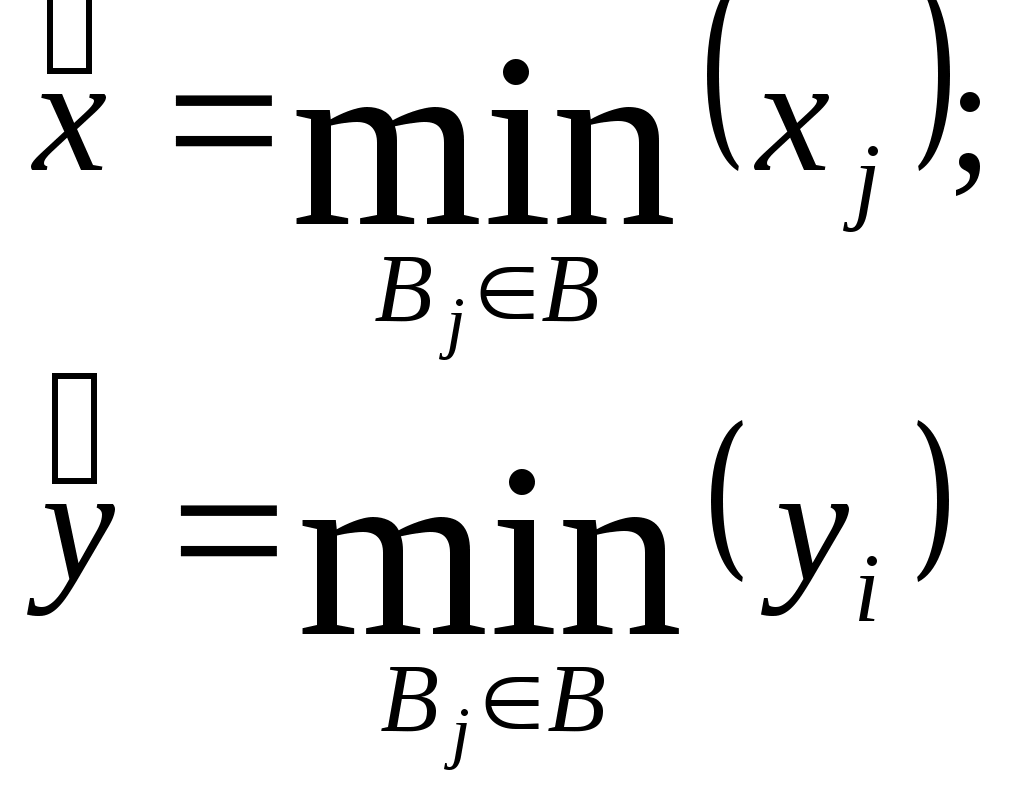,т.е.

(3.23)

5) пусть Х (у) будет максимальным (по В) числом субъектов, имеющих разрешенный (неразрешенный) доступ к любому 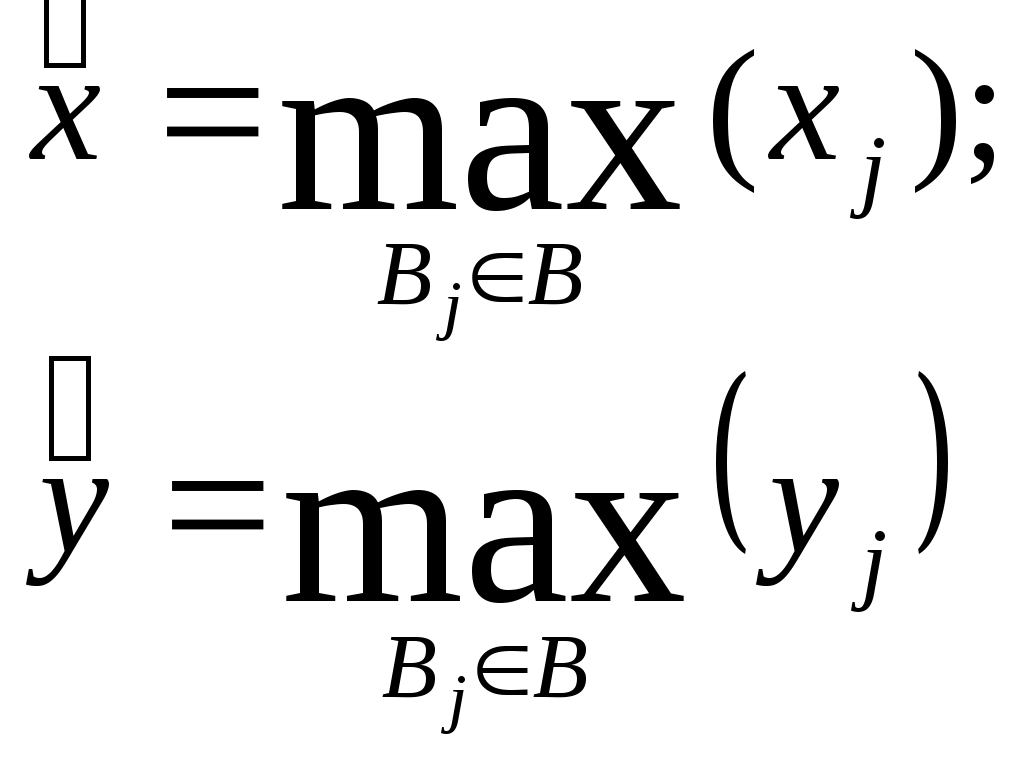, т.е.

(3.24)

Тогда качество распределения кодов доступа может быть оценено следующими показателями:

1) абсолютной степенью защиты

(3.25)

При этом _абс=1 будет только тогда, когда найдено такое распреде­ление, при котором неразрешенных доступов нет вообще; в противном случае _абс<1. Абсолютность данного показателя интерпретируется в том смысле, что его значение не зависит от количества субъектов и объектов, а меняется только в зависимости от среднего числа неразрешенных до­ступов;

2) относительной степенью защиты

(3.26)

0≤_отн≤1, причем _отн=1, если система не допускает неразрешенных доступов, а _отн=0, если система позволяет максимально возможное число неразрешенных доступов;

3) минимальной степенью защиты

(3.27)

4) максимальной степенью защиты

(3.28)

Доказано, что оптимальное распределение кода будет при минимальном числе наборов, разрешающих доступ. Это достигается при равномерном распределении субъектов по всем классам доступа.

Ниже приводятся результаты применения модели к иерархическим системам, причем под иерархическими понимаются такие системы, в которых данный субъект имеет разрешенный доступ ко всем объектам, доступ к которым имеют субъекты, стоящие в иерархии ниже данного. Рассмотрены три вида иерархии:

1) кольцевая структура, в которой субъекты представлены совокупностью концентрических колец, причем субъект, относящийся к внутрен­нему кольцу, имеет разрешенный доступ ко всем объектам, к которым имеют разрешенный доступ все субъекты, относящиеся к внешним (относительно данного) кольцам, а доступ в обратном направлении не должен разрешаться;

2) двоичная симметричная структура типа дерева, в которой каж­дый субъект представлен только одним узлом дерева, причем каждый субъект должен иметь разрешенный доступ ко всем объектам, к которым имеют разрешенный доступ все субъекты, расположенные ниже данного в иерархической структуре, но не имеют доступа к объектам, к которым имеют доступ субъекты более высоких уровней иерархии;

3) произвольные структуры с частичным упорядочением.

Для названных видов иерархии получены следующие результаты:

1) в системах с кольцевой структурой, в которых выполняется усло­вие /В/=/А/=U, с монотонным механизмом доступа при присвоение кода, удовлетворяющего сформулированным выше услови­ям кольцевой структуры, максимизирует абсолютную и относительную степень защиты при выполнении следующих условий: в присвоении ис­пользуется минимальных кодов объектов, где - так назы­ваемый уровень линейной иерархии (для различных механизмов доступа вычисляется по различным зависимостям и составляет 1 - 6); присвоение кодов осуществляется шаг за шагом, начиная с внутреннего кольца, до­бавляя каждый раз 1 бит, для чего разработана специальная алгоритми­ческая процедура; субъекты по кодам доступа распределяются с макси­мально возможной равномерностью;

2) в системах с двоичной симметричной структурой типа дерева оптимальное (т. е. удовлетворяющее условиям доступа в иерархии и максимизирующее абсолютную и относительную степени защиты) присвоение кодов доступа достигается итерационной процедурой, на каждом шаге которой объекты дерева делятся на два класса так, чтобы выделенные поддеревья находились в различных классах;

3) для произвольных иерархических структур с частичным упорядочением доказано, что нижней оценкой числа неразрешенных доступов

Является , где п - число узлов в иерархической структуре, а d- число возможных кодов доступа.

Рассмотрим далее теоретико-эмпирический подход к оценке уязвимости информации.

Ранее было показано, что все необходимые показатели уязвимости могут быть вычислены на основе так называемых базовых показателей.

По определению, базовым является показатель уязвимости информации в одном структурном компоненте АСОД относительно одного дестабилизирующего фактора и относительно одного нарушителя одной категории (для факторов, связанных со злоумышленными действиями людей).

Для определения базовых показателей уязвимости различных видов применяются так называемые аналитические модели, которые позволяют определять искомые величины (в данном случае - показатели уязвимости информации) путем проведения вычислений по заранее установленным (выведенным) зависимостям.

Аппаратура и материалы:

1. ПЭВМ