Эффективность проекта, критерии и методы оценки. Теоретикометодологические
 Скачать 361.4 Kb. Скачать 361.4 Kb.
|
|
r (1 n1 )(1 n2 )(1 n3 ) 1 Где n1 – реальная ставка ссудного процента; n2 – темп инфляции; n3 – вероятность риска. Определяем переменные: n1 – 8%; n2 – 8,7%; n3– не учитываем. r (1 0,8)(1 0,087) 1 1,08*1,087 1 0,17 (3) В соответствии с полученной ставкой вычисляем чистый дисконтированный доход: NPV 200 55 77 115 115 115 200 47,01 56,20 71,87 61,50 52,51 89,09 1,17 1,37 1,6 1,87 2,19 Таким образом, данный расчёт чистого дисконтированного дохода указывает на прибыльность проекта (т.к.NPV> 0). Индекс доходности: Для его определения используем дисконтированный доход, определённый в процессе вычисления NPV: PI Дисконтированные _ доходыДисконтированные_ инвестиции 289,09 1,44 200,00 (4) Индекс доходности превышает единицу. Таким образом, на основании полученных данных, в целом инвестиционный проект является прибыльным. Но для полнейшейоценки его эффективности, нам необходимо произвести оценку рисков инвестиционного проекта и выяснить эффективность проекта с их учётом.
ВООО «Рубин» используется несколько методов оценивания рисков инвестиционных проектов. Это – коррекция ставки дисконтирования, методика Монте-Карло (имитационное моделирование), анализ чувствительности инвестиционного проекта, дополняемый анализом безубыточности, а также использование статистических методов. Выбор способов оценки определяется полнотой информации, которая имеется в распоряжении аналитиков предприятия, а также уровнем квалификации специалистов-менеджеров. Произведём анализ рисков текущего инвестиционного мероприятия компании с учётом тех способов, которые применяются в ООО «Рубин». Сравнительный анализ оценок инвестиционного риска при изменении ставки дисконтирования. Для проведения сравнительного анализа произведём коррекцию ставки дисконтирования, включив в её состав показатель вероятности риска. Для данного инвестиционного проекта аналитиками завода вероятность риска оценивается в 2%. Рассчитаем новую ставку дисконтирования с учётом риска: r (1 0,8)(1 0,087)(1 0,02) 1 1,08*1,087 *1,02 1 0,197 Рассчитаем новое значение чистого дисконтированного дохода: NPV 200 55 1,197 77 1,433 115 1,715 115 2,053 115 2,457 69,57 Чистый дисконтированный доход снизился незначительно (89,09 – 69,57 = 19,52), проект по-прежнему остаётся прибыльным. Дополнительно определим индекс доходности, в соответствии с изменённым дисконтированным доходом: PI Дисконтированные _ доходыДисконтированные_ инвестиции 269,57 1,35 200,00 Произведём сравнительный анализ показателей, определённых без учёта риска и с его учётом (табл. 4). Таблица 4 - Сравнительный анализ показателей эффективности инвестиционного проекта с учётом и без учёта рисков
Таким образом, при коррекции ставки дисконтирования с учётом риска получаемые показатели оценки эффективности инвестиционного проекта изменяются незначительно. Значения показателей сохраняют соблюдение требований эффективности (прибыльности) инвестиционного проекта, а именно: NPV> 0; PI> 1. Анализ чувствительности инвестиционного проекта Произведём оценку чувствительности инвестиционного проекта к одновременному изменению отпускных цен и объёма продаж. Необходимо определить множество комбинаций соотношения цен и объёма продаж, которые обеспечат получение как минимум неотрицательного значения чистой приведённой стоимости, т.е. NPV ≥ 0. В целях оценки данным методом расширим формулу чистой приведённой стоимости, т.е. учтём в ней переменные: цены и объём продаж. Формула NPV принимает вид: NPV S (c k)X(1 r)1 (c k)X(1 r)2 (c k)X(1 r)3  O (c k)X (1 r)4 (c k)X (1 r)5 Где S0 – инвестиционные затраты; r – ставка дисконтирования; k– приведённые издержки на единицу продукции Значения с и Х – это неизвестные переменные«цена» и «объём продаж» соответственно. Далее необходимо определить множество допустимых комбинаций выбранных неопределённых переменных: отпускной цены и объёма продаж. Для формирования этих комбинаций используется указанная выше расширенная формула расчёта NPV (зависящего главным образом от этих двух неопределённых переменных) при условии, что NPV = 0. Числовые значения, необходимые для расчёта используем в соответствии с данными аналитического отдела (S0иk) и нашими расчётами выше ®: S0 – 200 000 000; r – 0,197; k – 551,25. При подстановке числовых значений получаем равенство: 0 200000000 (c 551,25)Х*1,1971 (с 551,25)Х*1,1972 (с 551,25)Х*1,1973 (с 551,25)Х*1,1974 (с 551,25)Х*1,1975; Рассчитаем равенство, которое позволит выделить искомые комбинации с и Х, получим с помощью следующих алгебраических преобразований: (с 551,25) Х (с 551,25) Х*1,197 (с 551,25) Х*1,1972 200000000 1,1975 ; (с 551,25) Х*1,1973 (с 551,25) Х*1,1974 200000000 *1,1975 1,1975 (с 551,25) Х 1,1976 (с 551,25) Х 1,1977 (с 551,25) Х 1,1978 (с 551,25) Х 1,1979 (с 551,25) Х; 491474180 (2,457с1354,63) Х (2,941с1621,49) Х (3,521с1940,92) Х (4,215с 2323,28) Х (5,045с 2780,97) Х; 491474180 Х(2,457с1354,63 2,941с1621,49 3,521с1940,92 4,215с 2323,28 5,045с 2780,97); 491474180 Х(18,179с10021,29) Х 491474180 ; 18,179с10021,29 Х 27035270 ; с 551,26 Последнее равенство позволит рассчитать объёмы продаж при заданных уровнях отпускной цены. При этом необходимо учесть уровень цены, рассчитанный аналитиками – 735 руб. и относительно этой цены представить те варианты цен, которые будут отличаться от данной как в сторону снижения, так и в сторону увеличения. Расчёты представлены в таблице 5. Таблица 5 - Расчёт объёмов продаж при заданных уровнях цен
Результаты расчёта позволяют графически изобразить искомые комбинации Х и с (рис. 1). На оси ординат отмечены уровни цен, а на оси абсцисс – объёмы продаж. На основании данных таблицы 5 построена кривая, отображающая комбинации отпускных цен и продаж, при которыхNPV= 0. 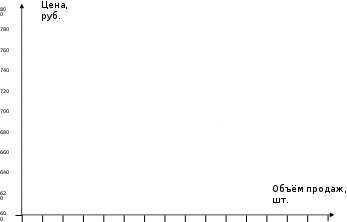                100 000 110 000 120 000 130 000 140 000 150 000 160 000 170 000 180 000 190 000 200 000 210 000 220 000 230 000 240 000 Рисунок 1. Зависимость объёма продаж от отпускной цены Выше кривой находится область, в которой любые комбинации с и Х гарантируют получение положительных дисконтированных потоков денежных средств в период эксплуатации инвестиций. Т.е. в этой области соблюдается неравенство: NPV> 0. Согласно утверждениям специалистов, наклон кривых чувствительности к оси абсцисс на графиках, составленных при соответствующем анализе, даёт представление о величине и направлении чувствительности проекта к изменению каждой из анализируемых базовых переменных. Чем больше угол наклона прямой к оси абсцисс, тем более чувствительно значение NPV к любым изменениям базовых переменных. В нашем случае угол наклона кривой составляет менее 900. То есть эффективность проекта, измеряемая значением NPV не слишком чувствителен к изменению объёмов продаж. Далее дополним анализ чувствительности инвестиционного проекта нахождением порога рентабельности (точки безубыточности) – в количественном и стоимостном аспектах. Определение порога рентабельности математическим методом: Определим объём реализации (WS): WS 2595918* 735 1907999730 Далее рассчитаем совокупные издержки (КС): KC 500856418,92 2595918*358,31 500856418,92 930143378,58 1430999797,50 Определим порог рентабельности (ВЕР): в количественном выражении: BEP 500856418,92 500856418,92 1329625шт. 735 358,31 376,69 в стоимостном выражении: BEP' 1329625* 735 977274375 руб. Таким образом, при объёме продаж в 1329625 шт. и объёме реализации в 977 274 375 руб. компания не будет иметь ни прибылей, ни убытков. Далее вычислим порог рентабельности как степени использования производственного потенциала или степени удовлетворения ожидаемого спроса. Он выражается в процентах: ВЕР'' 500856418,92 3757222 *(735 358,31) 500856418,92 3757222 * 376,69 500856418,92 1415307955,18 0,3539 *100% 35,39% ВЕР'' 1329625 0,3539 *100% 35,39% 3757222 Таким образом, при достижении безубыточно-бесприбыльного уровня производства производственный потенциал компании будет использоваться только 35,39%. Что говорит о том, что оставшиеся 64,61% производственных мощностей являются уже прибыльным потенциалом. Теперь определим точку безубыточности с помощью графического метода, что позволит сравнить график продаж с графиком совокупных издержек (рис. 2). За основу объёма продаж можно взять как показатель максимально возможного количества проданных изделий (Im), так и показатель, рассчитанный на основании бизнес-плана инвестиционного проекта, основанный на анализе спроса. В построение графика безубыточности использован второй показатель. Определим значение коэффициента безопасности (WВ): для объёма продаж, рассчитанного на основании анализа спроса: W 2595918 1329625 1266293 0,50 B2595918 2595918 для объёма продаж, основанного на производственных мощностях: W 3757222 1329625 2427597 0,65 B3757222 3757222 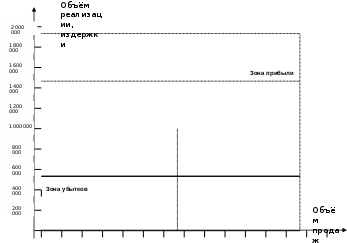               200 000 400 000 600 000 800 000 1 000 000 1 200 000 1 400 000 1 600 000 1 800 000 2 000 000 2 200 000 2 400 000 2 600 000 2 800 000 Рисунок 2. Определение порога рентабельности графическим методом Показатели коэффициента безопасности дают оптимистичные прогнозы: значение показателя для объёма продаж на основании спроса, значение показывает, что падение спроса даже на 50% не принесёт ни убытков,ни доходов. Значение показателя, основанного на возможностях производства ещё выше. Измерение риска с использованием показателя дисперсии Приведем расчёты первых двух этапов применения данного метода: определение математического ожидания потоков денежных средств и расчёт математического ожидания NPV. ЭтапI. Расчёты производятся на основании заданных вероятностей возможных потоков денежных средств, связанных с инвестициями, представленными в таблице 7. Таблица 7 - Распределение вероятностей независимых от времени потоков денежных средств, связанных с инвестиционным проектом ООО «Рубин»
Рассчитаем математическое ожидание потоков денежных средств для каждого года: E(S1) 55* 0,06 63* 0,2 46 * 0,3 33 12,6 13,8 59,4 E(S2 ) 77 * 0,4 55* 0,2 63* 0,3 85* 0,1 30,8 1118,9 8,5 69,2 E(S3 ) 115* 0,6 70 * 0,05 96 * 0,15 125* 0,2 69 3,5 14,4 25 111,9 E(S4 ) 115* 0,7 85* 0,1110 * 0,2 80,5 8,5 22 111 E(S5 ) 115* 0,8 100 * 0,15 120 * 0,05 92 15 6 113 Рассчитаем математическое ожиданиеNPV: E(NPV) 200 59,4 1,197 69,2 1,4328 111,9 1,7151 111 2,0529 113 2,4574 200 49,62 48,30 65,24 54,07 45,98 63,21 Математическое ожидание для NPV для инвестиционного проекта ООО «Рубин»является положительным, т.е. проект окупается. Дальнейшие этапы – составление комбинаций денежных средств, расчёт дисперсии,расчёт стандартного отклоненияNPVи определение коэффициента вариацииNPVв данной работе осуществить не удастся в связи со сложностью и объёмностью расчётов. Так, количество комбинаций потоков денежных средств составляет 432. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
