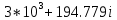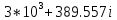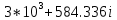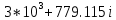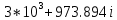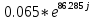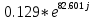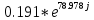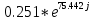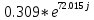Главная страница
Навигация по странице:

  • «Московский технический университет связи и информатики»

  • «Исследование пассивных цепей при гармоническом воздействии на постоянной частоте» по дисциплине «Теория электрических цепей»

    		•

    Исследование пассивных цепей при гармоническом воздействии на постоянной частоте. лаб32. Теория электрических цепей


    Скачать 2.9 Mb.
    НазваниеТеория электрических цепей
    АнкорИсследование пассивных цепей при гармоническом воздействии на постоянной частоте
    Дата22.03.2022
    Размер2.9 Mb.
    Формат файлаdocx
    Имя файлалаб32.docx
    ТипЛабораторная работа
    #410017


    МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ

    КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

    Ордена Трудового Красного Знамени федеральное государственное

    бюджетное образовательное учреждение высшего образования

    «Московский технический университет связи и информатики»




    Кафедра «Теория электрических цепей»


    Лабораторная работа № 32

    «Исследование пассивных цепей при гармоническом воздействии на постоянной частоте»

    по дисциплине

    «Теория электрических цепей»

    Выполнила: студентка гр. БИК2101

    Мамутова А.В.

    Вариант №18

    Москва, 2021 г.

    Оглавление


    Цель работы: 2

    Предварительный расчет 3

    Работа в Micro-Cap 6

    Вопросы для самопроверки 11



    Цель работы:


    С помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.

    Предварительный расчет


    1.1 Рассчитать в алгебраической форме комплексное сопротивление конденсатора Zc, определить его полное сопротивление |Zc| (модуль) и аргумент arg|Zc| (фазу) на пяти частотах 1, 2, 3, 4 и 5 кГц, если С=38,7 нФ.

    По предварительному расчету
    Получено экспериментально

    f, кГц
    С, нФ
    Zс, Ом
    |Zс|, Ом
    arg|Zс|, град.
    |Zс|, Ом
    arg|Zс|, град.

    1
    38.7
    -j4113
    4113
    -90
    4113
    -90

    2
    38.7
    -j2056
    2056
    -90
    2056
    -90

    3
    38.7
    -j1371
    1371
    -90
    1371
    -90

    4
    38.7
    -j1028
    1028
    -90
    1028
    -90

    5
    38.7
    -j822.506
    822.506
    -90
    822.506
    -90

    Таблица 1

    1.2 Рассчитать в алгебраической форме комплексное сопротивление Zrc RC-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, С=38,7 нФ.

    По предварительному расчету
    Получено экспериментально

    f, кГц
    С, нФ
    R, кОм
    Zrс, Ом
    |Zrс|, Ом
    arg|Zrс|, град.
    |Zrс|, Ом
    arg|Zrс|, град.

    1
    38.7
    3
    3000-j4113
    8755
    -53.89
    8755
    -53.89

    2
    38.7
    3
    3000-j2056
    3637
    -34.428
    3637
    -34.428

    3
    38.7
    3
    3000-j1371
    3298
    -24.588
    3298
    -24.588

    4
    38.7
    3
    3000-j1028
    3171
    -18.917
    3171
    -18.917

    5
    38.7
    3
    3000-j822.506
    3111
    -15.332
    3111
    -15.332

    Таблица 2

    1.3 Рассчитать напряжения на конденсаторе U2=U2e^j , если U1=0,707e^j0 на частотах 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу

    По предварительному расчету
    Получено экспериментально

    f, кГц
    С, нФ
    R, кОм
    U1, В
    U2, В
    , град.
    U2, В
    U2, В
    , град.

    1
    38.7
    3
    0.707
    0.94
    -36.11
    0.94*e-j36,11º
    0.94
    -36.11

    2
    38.7
    3
    0.707
    0.565
    -55.572
    0,565*e-j52,5º
    0.565
    -55.572

    3
    38.7
    3
    0.707
    0.416
    -65.442
    0,416*e-j62,9º
    0.416
    -65.442

    4
    38.7
    3
    0.707
    0.324
    -71.083
    0,324*e-j69º
    0.324
    -71.083

    5
    38.7
    3
    0.707
    0.264
    -74.668
    0,264*e-j72,9º
    0.264
    -74.668

    Таблица 3

    1.4 Рассчитать в экспоненциальной форме комплексное сопротивление катушки индуктивности ZL для пяти частот 1, 2, 3, 4 и 5 кГц, определить её полное сопротивление и аргумент, если L=31 мГн.

    По предварительному расчету
    Получено экспериментально

    f, кГц
    L, мГн
    ZL, Ом
    |ZL|, Ом
    arg|ZL|, град.
    |ZL|, Ом
    arg|ZL|, град.

    1
    31
    j194.782
    194.782
    90
    194.782
    90

    2
    31
    j389.559
    389.559
    90
    389.559
    90

    3
    31
    j584.337
    584.337
    90
    584.337
    90

    4
    31
    j779.115
    779.115
    90
    779.115
    90

    5
    31
    j973.894
    973.894
    90
    973.894
    90

    Таблица 4

    1.5 Рассчитать в алгебраической форме комплексное сопротивление ZRL RL-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, L=31 мГн.

    По предварительному расчету
    Получено экспериментально

    f, кГц
    L, мГн
    R, кОм
    ZL, Ом
    |ZL|, Ом
    arg|ZL|, град.
    |ZL|, Ом
    arg|ZL|, град.

    1
    31
    3


    3006
    3.715
    3006
    3.715

    2
    31
    3


    3025
    7.399
    3025
    7.399

    3
    31
    3


    3056
    11.022
    3056
    11.022

    4
    31
    3


    3100
    14.558
    3100
    14.558

    5
    31
    3


    3154
    17.985
    3154
    17.985

    Таблица 5

    1.6 Рассчитать напряжения на катушке индуктивности U2=U2e j , если U1=0,707e j0 для пяти частот 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу.

    По предварительному расчету
    Получено экспериментально

    f, кГц
    L, мГн
    R, кОм
    U1, В
    U2, В
    , град.
    U2, В
    U2, В
    , град.

    1
    31
    3
    0.707
    0.065
    86.285


    0.065
    86.285

    2
    31
    3
    0.707
    0.129
    82.601


    0.129
    82.601

    3
    31
    3
    0.707
    0.191
    78.978


    0.191
    78.978

    4
    31
    3
    0.707
    0.251
    75.442


    0.251
    75.442

    5
    31
    3
    0.707
    0.309
    72.015


    0.309
    72.015

    Таблица 6

    Работа в Micro-Cap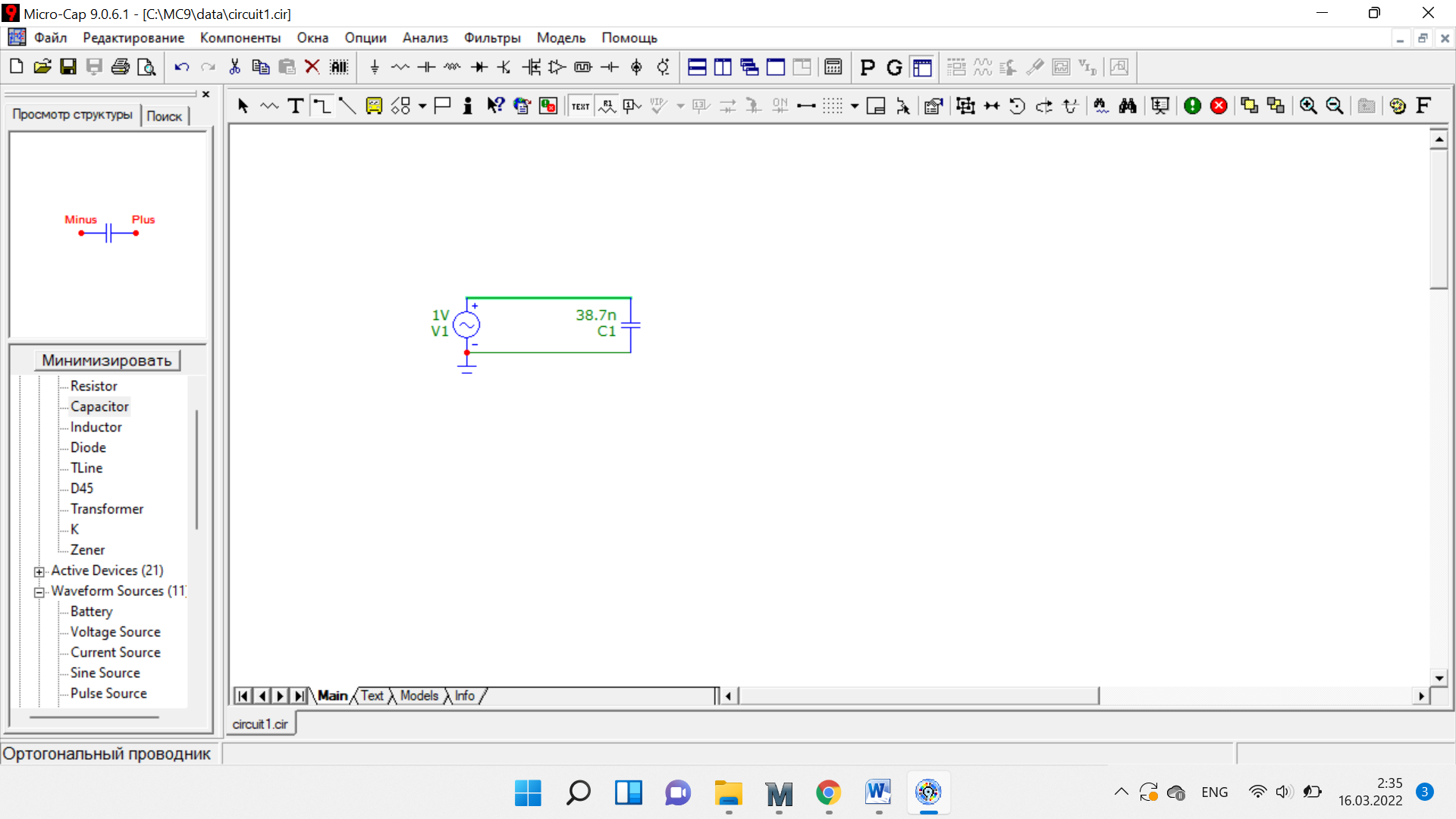




    Рисунок 1 - схема с источником синусоидального напряжения и конденсатором

    1.1 Исследование модуля и фазы комплексного сопротивления C-цепи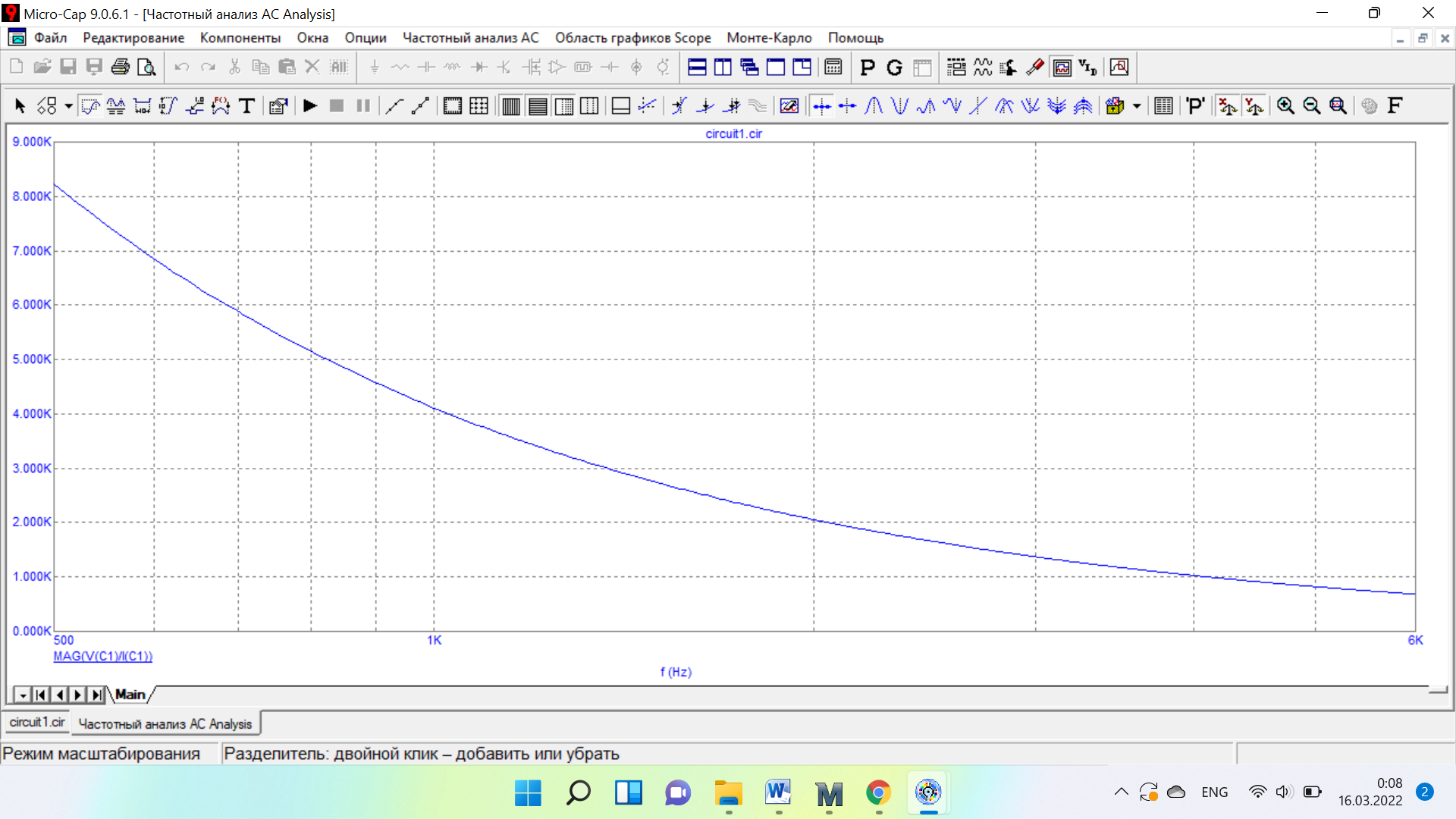

    Рисунок 2 - зависимость модуля комплексного сопротивления конденсатора от частоты

    Рисунок 3 - зависимость модуля фазы входного сопротивления от частоты



    Рисунок 4 - схема с источником синусоидального напряжения, резистором и конденсатором

    4.2 Исследование модуля и фазы комплексного сопротивления RC-цепи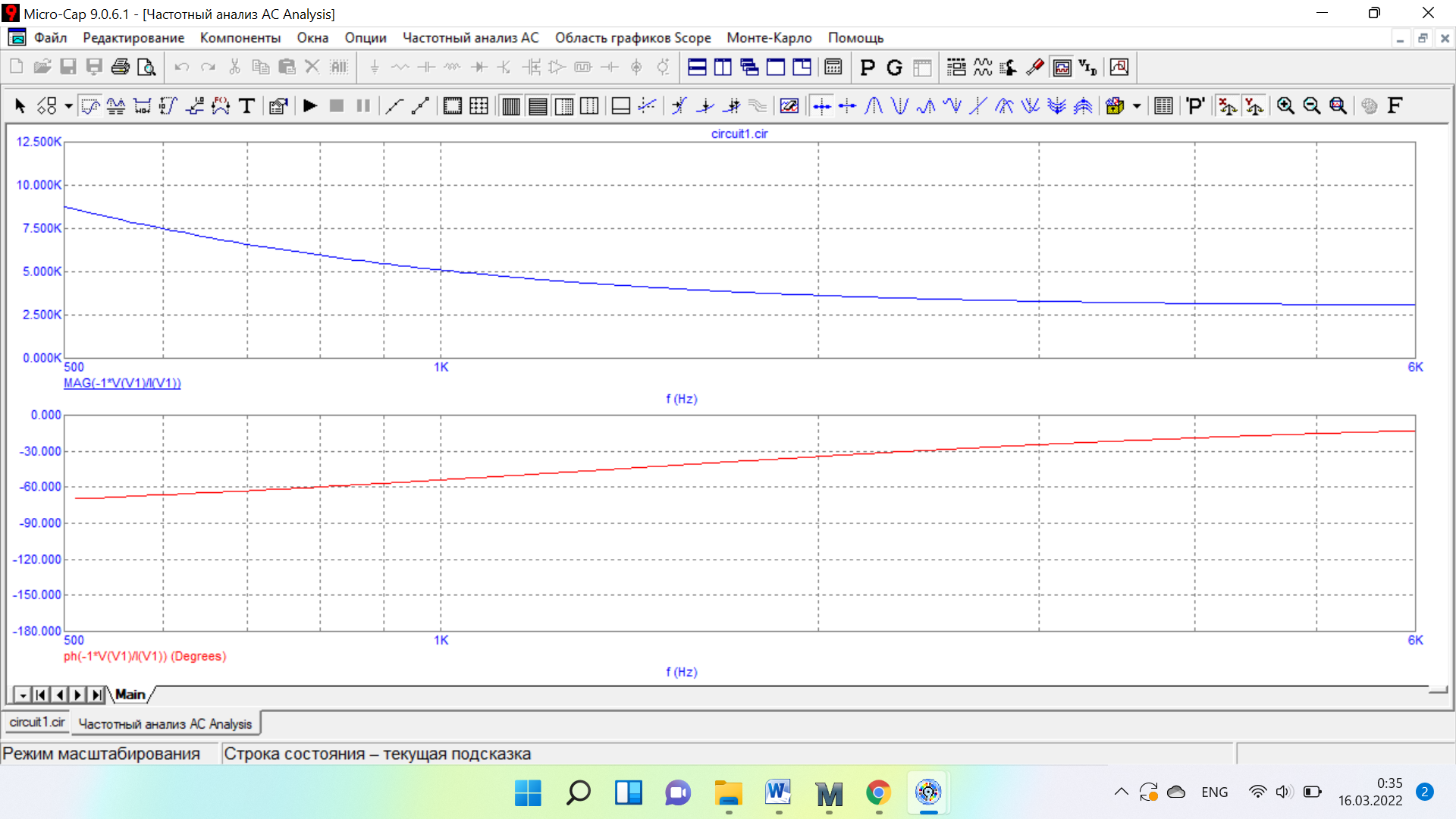



    Рисунок 5 - зависимость модуля и фазы комплексного сопротивления RC-цепи от частоты

    4.3 Исследование модуля и фазы комплексного напряжения на конденсаторе RC-цепи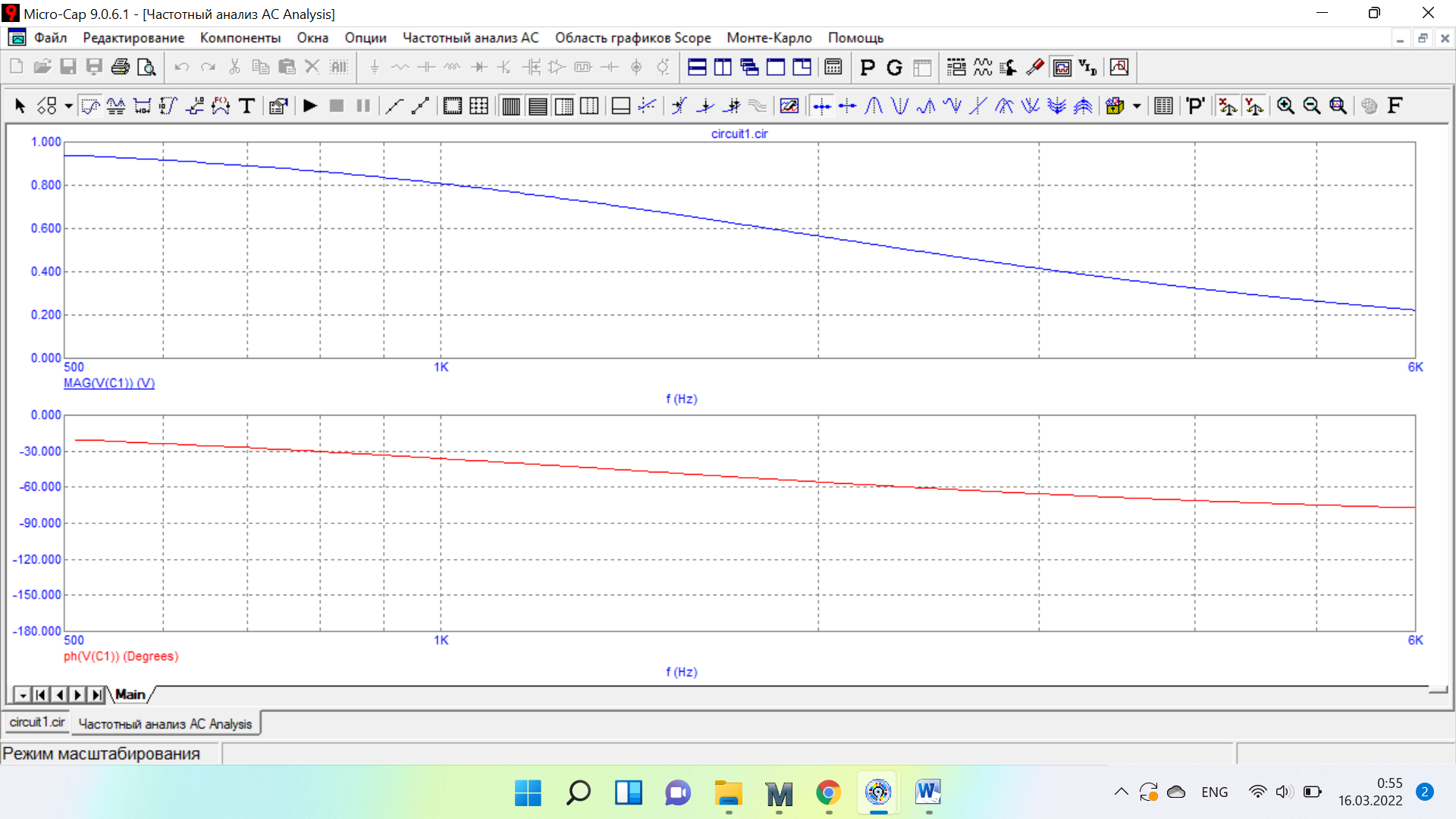



    Рисунок 6 - зависимость модуля и фазы комплексного напряжения на конденсаторе U2 в RC-цепи от частоты



    Рисунок 7 – схема с источником синусоидального напряжения и катушкой

    4.4 Исследование модуля и фазы комплексного сопротивления L-цепи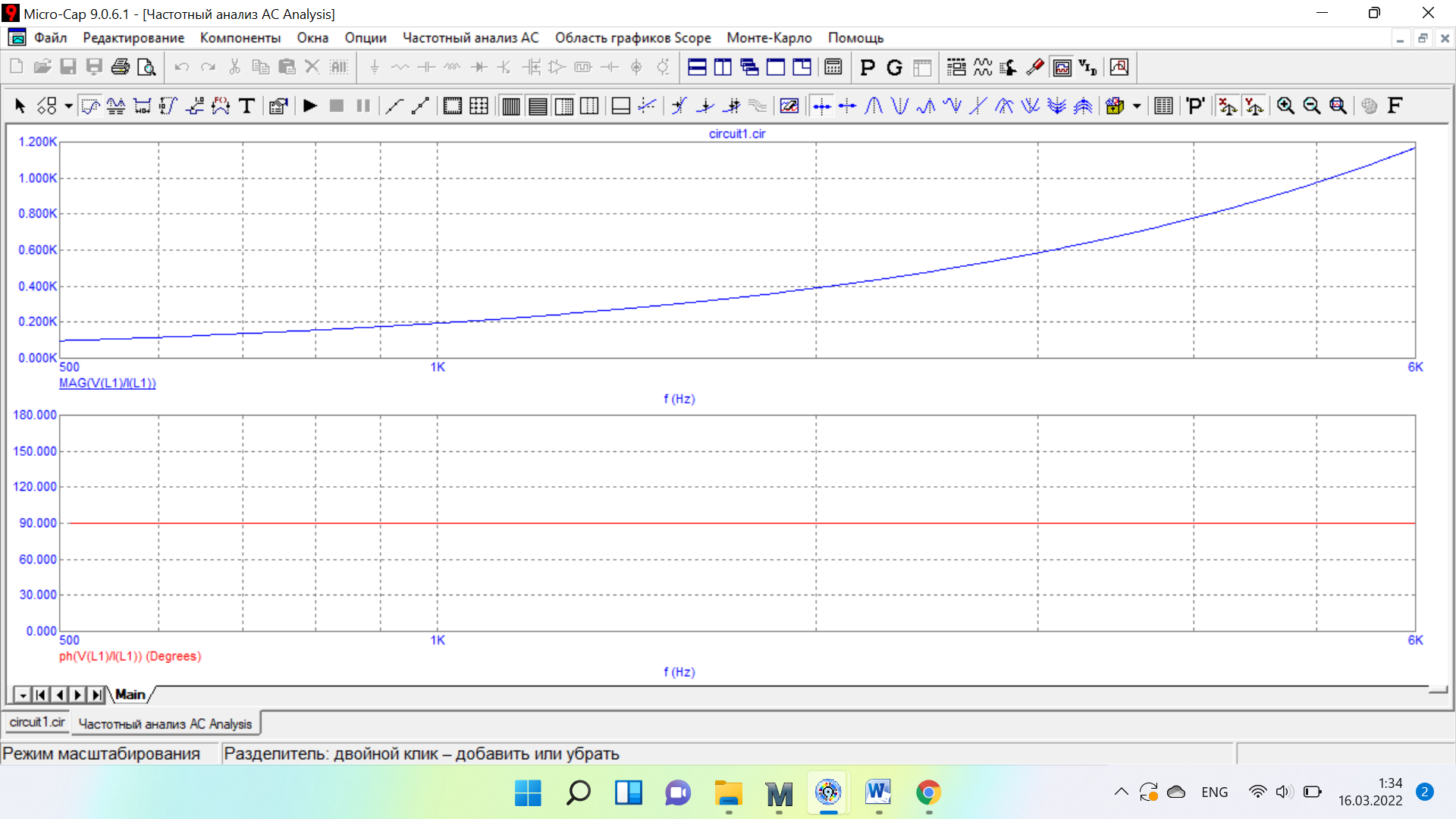



    Рисунок 8 - зависимость модуля и фазы комплексного сопротивления катушки от частоты



    Рисунок 9 – схема с источником синусоидального напряжения, резистором и катушкой

    4.5 Исследование модуля и фазы комплексного сопротивления RLцепи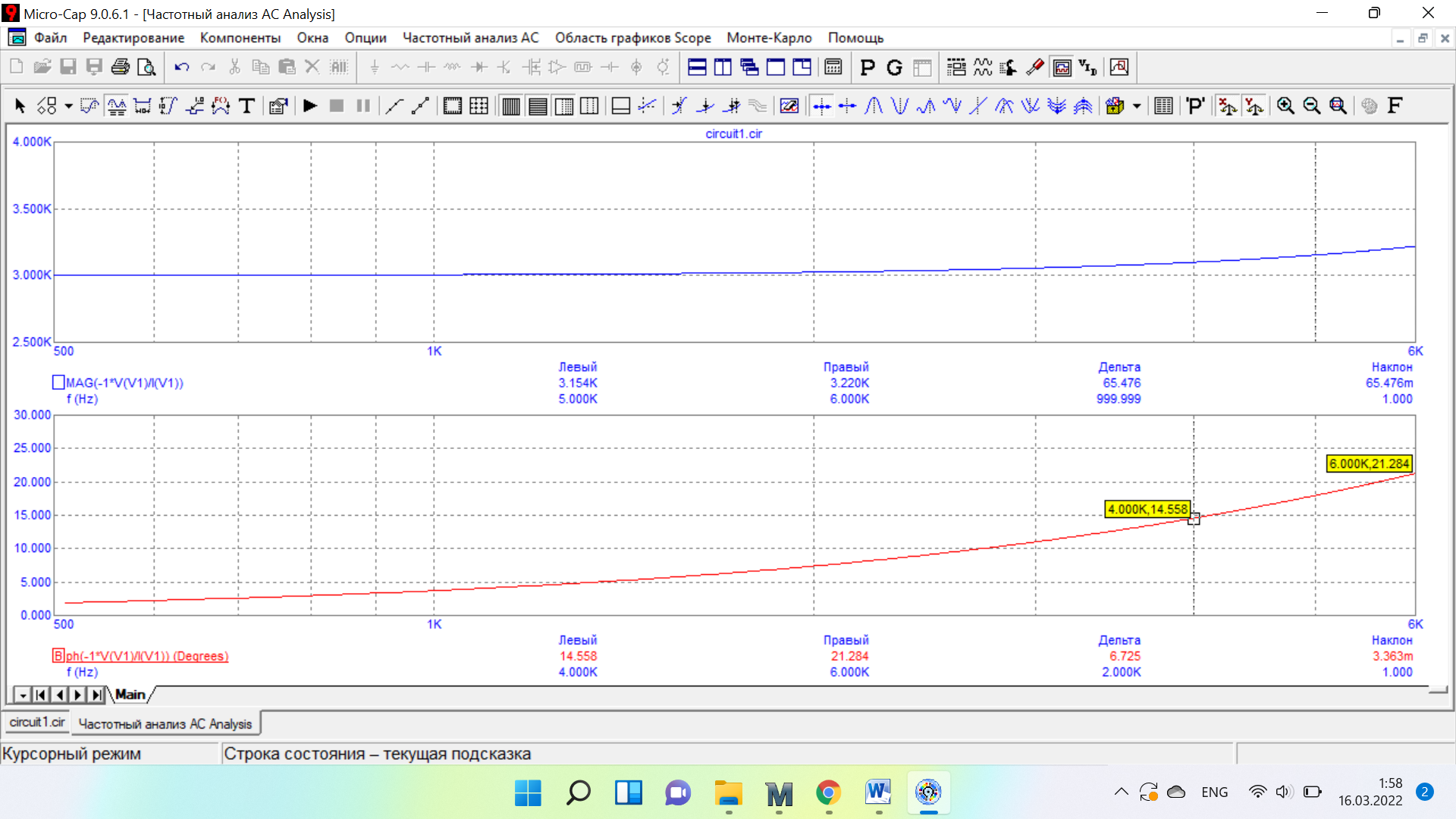



    Рисунок 7 - зависимость модуля и фазы комплексного сопротивления RL-цепи от частоты

    4.6 Исследование модуля и фазы комплексного напряжения на катушке RL-цепи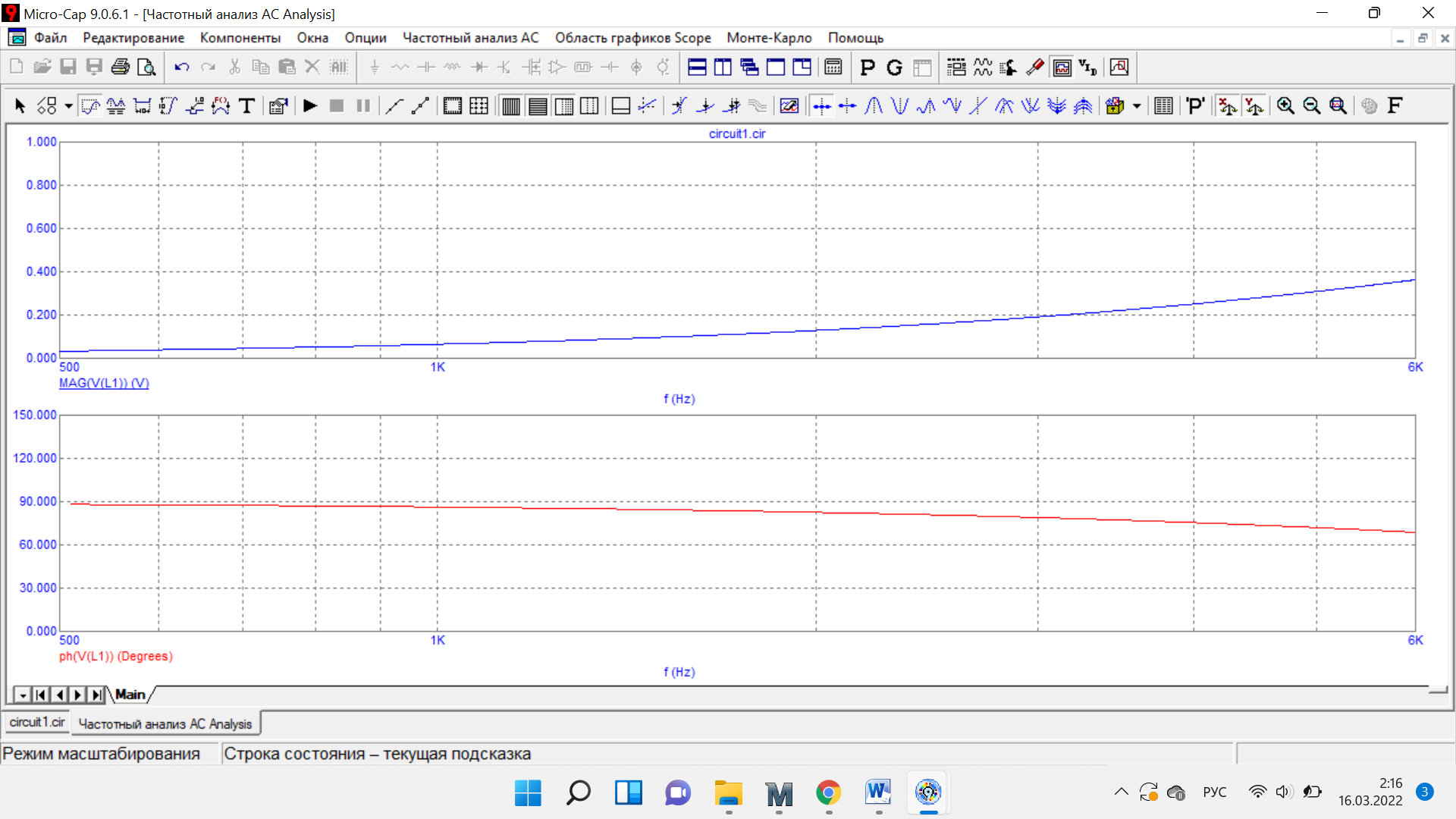



    Рисунок 8 - зависимость модуля и фазы комплексного напряжения на катушке RL-цепи от частоты

    Вопросы для самопроверки


    1. Граничной называется частота, при которой модуль реактивного сопротивления равен резистивному сопротивлению.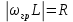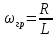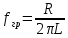

    , , .

    1. Каково значение модуля входного сопротивления RL-цепи на граничной частоте?

    На граничной частоте модуль входного сопротивления RL-цепи: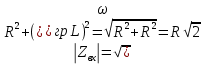

    .

    1. Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?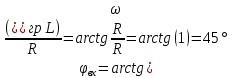

    .

    1. К чему стремится модуль тока RL-цепи при увеличении частоты?

    При увеличении частоты увеличится индуктивное сопротивление, соответственно увеличится модуль входного сопротивления. Модуль тока RL-цепи будет уменьшаться и стремится к 0.

    1. Чему равен модуль входного сопротивления RL-цепи при частоте равной нулю?

    При частоте равной нулю модуль входного сопротивления RL-цепи равен R.

    написать администратору сайта