Грунты. Теория определения напряжений
 Скачать 49.14 Kb.
|
|
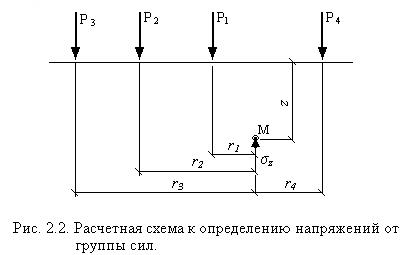
Теория определения напряжений основывается на представлении о способах передачи нагрузок на грунты и гипотезе о закономерностях их распределения в грунтовом массиве. Нагрузки на грунты фактически передаются по площадкам различной конфигурации в виде произвольно изменяющихся давлений. Само давление, сложное по своей сути, представляет нагружение, которое можно свести к нагружению простыми силами. Элементарным видом нагрузки, служащим основой для таких преобразований, является сосредоточенная сила. Решение для определения напряжений от сосредоточенной силы позволяет находить напряжения от группы сил путем суммирования напряжений от каждой из них (метод элементарного суммирования). Идея суммирования используется при нахождении напряжений от распределенной нагрузки. Для этого площадка расчленяется на участки, давление в каждом из них в точке приложения равнодействующей заменяется сосредоточенными силами. Теоретические методы определения напряжений могут применяться при определенных условиях, связанных с грунтами. Грунтовый массив, сложенный разнообразными по происхождению, виду, залеганию и состоянию грунтами, идеализируется. Предполагается, что различиям между грунтами мало влияют на распределение напряжений и ими можно пренебречь. Аналитические решения для разных видов нагрузок получены при допущениях: • грунтовый массив считается однородным, сплошным, изотропным, материалом; • при загружении грунтовый массив деформируется линейно. Предметом самостоятельно изучения являются методы определения вертикальных напряжений σz, которые используются в расчетах осадки, от следующих видов нагрузок: • от сосредоточенной силы; • от группы сосредоточенных сил (метод элементарного суммирования); • от равномерно распределенной нагрузки по прямоугольной площадке с различным соотношением сторон. 2.1. Напряжения от сосредоточенной силы на поверхности грунта. При выводе формулы для определения напряжений распределительная способность грунтового массива фактически была задана исходя из гипотез: напряжения в любой точке М уменьшаются с увеличением расстояния от неё до точки приложения силы;
при изменении положения точки М напряжения изменяются по закону косинуса угла β (рис. 2.1). С исходным выражением и проделанными преобразованиями можно познакомиться по учебнику [1]. Из всех компонентов напряжений в расчетах используются только вертикальные нормальные напряжения σz. В любой произвольно взятой точке М напряжения σz вычисляются по формуле: σz = kР/z2, 2.1) где k – коэффициент, подсчитываемый по формуле k = 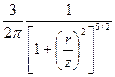 , (2.2)или принимается по табл. (2.1) в зависимости от отношения декартовых координат точки М r / z. Таблица 2.1 Значения коэффициента k
Примечания. Более подробная таблица коэффициентов k имеется в справочнике проектировщика «Основания и фундаменты». М.: 1964 г. 2.2. Напряжения σz от группы сил.
От нескольких сил напряжения в некоторой точке М определяются в соответствии со схемой на рис 2.2. Величина напряжения вычисляется как сумма напряжений σz от каждой силы по формуле σz = k1 Р1 /z2+ k2 Р2/z2+ k3 Р3 /z2+… ki Рi/z2 = ∑ ki Рi/z2 (2.3) где k1, k2, k3… ki– коэффициенты, принимаемые в зависимости от ri / z по табл. 2.1. r1, r2, r3…ri – расстояния от точки М до сил соответственно Р1, Р2, Р3…Рi. Вертикальных сил может быть сколь угодно. Величины сил и расстояния от них до точки М могут быть одинаковыми или разными. Данный случай определения напряжений принято называть метод элементарного суммирования. На практике он находит применение при загружении площадок произвольной формы и любом распределении передаваемого на грунт давления. Задание 2.1. Найти величину напряжений в точке М от сосредоточенных сил, расположенных как на рис. 2.2. Силы имеют одинаковую величину Р. Глубина расположения точки М, расстояния от неё до сил ri указаны в табл. 2.2. Величины напряжений σz при проведении вычислений находить с точностью до целых. Таблица 2.2 Исходные данные для выполнения задания
Пример 2.1. 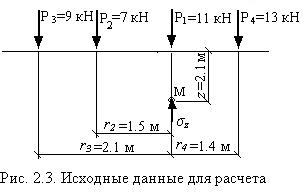 Определить напряжение в точке от сосредоточенных сил, показанных на рис. 2.3.Напряжение от силы Р1 = 11 кН, r1 = 0. При r1 / z = 0 по табл. .2.1 k1 = 0.4775. σz1 = 0.4775×11/2.12 =1.21 кПа. Напряжение от силы Р2 = 7 кН; r2 = 1.5 м. r2 / z = 1.5 /2.1 = 0.714. k2 = 0.17. σz2 = 0.17×7/2.12 = 0.27 кПа. Напряжение от силы Р3 = 9 кН; r3 = 2.1 м. r3 / z = 2.1 /2.1 = 1, k2 = 0.0844. σz3 = 0.0844×9/2.12 = 0.17 кПа. Напряжения от силы Р4 = 13 кН; r4 = 1.4 м. r4 / z = 1.4 /2.1 = 0.666, k4 = 0.191. σz4 = 0.191×13/2.12 =0.56 кПа. σzм = 1.21+0.27+0.17+0.56 = 2.21 кПа. 2.3 Напряжения от равномерно распределенного давления. Такой вид нагрузки на грунты самый частый в инженерных расчетах осадки фундаментов. Загруженная площадка имеет прямоугольную ф |
