Метод множників Лагранжа з фіксованими кінцями. МЕТОД МНОЖНИКІВ ЛАГРАНЖА ЗАДАЧА З ФІКСОВАНИМИ КІНЦЯМИ_УКР. Теорія оптимальних систем автоматичного управління
 Скачать 0.76 Mb.
|
|
ТЕОРІЯ ОПТИМАЛЬНИХ СИСТЕМ АВТОМАТИЧНОГО УПРАВЛІННЯ Наведено короткі теоретичні відомості, алгоритм та приклад розв'язання задачі за допомогою методу множників Лагранжа. Дано завдання за варіантами, розраховані на застосування програмного пакета для наукових та інженерних розрахунків Matlab. КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ МЕТОД МНОЖИКІВ ЛАГРАНЖА Метод множників Лагранжа дозволяє вирішити задачу оптимального управління, постановка якої у загальному випадку має вигляд: Рівняння руху об'єкта управління  де 𝐱 = (𝑥1 𝑥2 … 𝑥𝑛)𝑇 – вектор фазових координат,  – вектор змінних управління.Рівняння руху об'єкта управління повинні бути приведені до диференціальних рівнянь першого порядку, розвязаних відносно похідних всіх фазових координат 𝑥𝑖. Таким чином, кількість диференціальних рівнянь співпадає з кількістю фазових координат 𝑛. Обмеження  Обмеження є алгебраїчними рівняннями, яким повинні задовольняти фазові змінні та змінні управління. Обмеження можуть бути відсутніми (тобто 𝑙 = 0), якщо всі процеси, що відбуваються в об'єкті управління, описані за допомогою диференціальних рівнянь. Граничні умови  У задачі з фіксованими кінцями всі фазові координати задані в початковий 𝑡0 та кінцевий 𝑡𝑓 моменти часу. Таким чином, буде 2𝑛 граничних умов. У задачі з рухомим кінцем відсутні одна або кілька граничних умов і їх буде менше, ніж 2𝑛. У загальному випадку граничні умови мають вигляд  де 𝑞 ≤ 𝑛 – кількість граничних умов. Критерій оптимальності 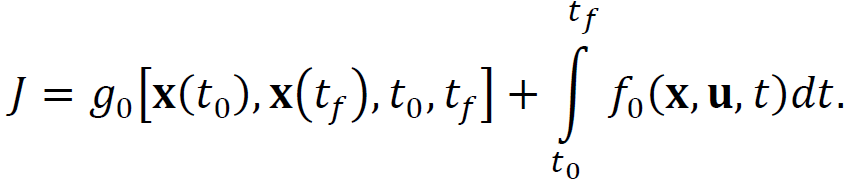 Критерій оптимальності у загальному випадку включає термінальний доданок 𝑔0 і інтегральний. Термінальний доданок може бути присутнім тільки в задачі з рухомим кінцем або нефіксованим часом, так як в задачі із закріпленими кінцями і фіксованим часом виключена варіація величин  Алгоритм розв'язання такої задачі включає такі дії: 1) Скласти гамільтоніан  При 𝑙 = 0 друга сума відсутня. Множник Лагранжа 𝜓0 = −1. 2) Скласти рівняння Ейлера-Лагранжа 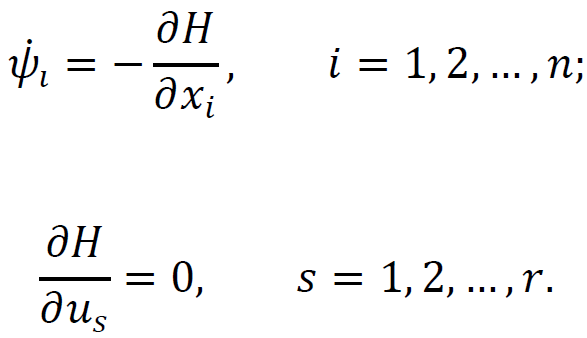 Останні рівняння називають умовою стаціонарності. 3) Виразити управляючі змінні 𝑢𝑠 (𝑠 = 1, 2, … , 𝑟) з умови стаціонарності та підставити в рівняння руху та рівняння Ейлера-Лагранжа. Вийде система диференціальних рівнянь: 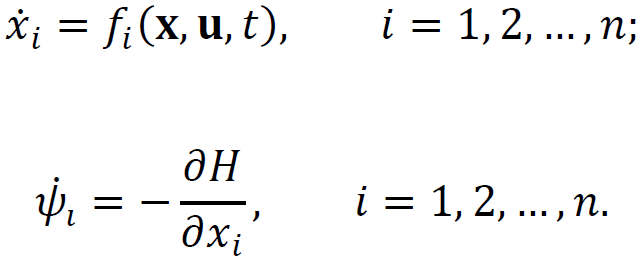 4) Розв'язати цю систему рівнянь з урахуванням граничних умов. У разі відсутності деяких граничних умов (завдання з рухомим кінцем) записуються умови трансверсальності: 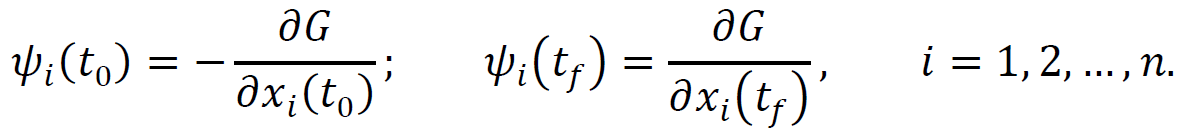 Для задачі з нефіксованим часом складаються умови трансверсальності, зумовлені варіацією початкового або кінцевого моменту часу: 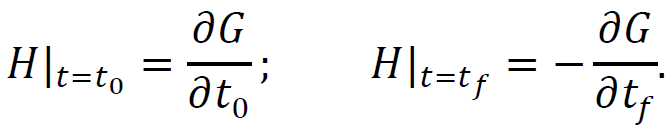 Кількість граничних умов та умов трансверсальності має співпадати з кількістю постійних інтегрування, тобто з кількістю диференціальних рівнянь. Знайти постійні інтегрування. 5) Підставити знайдені постійні інтегрування у вирази для 𝑥𝑖(𝑡) і 𝜓𝑖(𝑡), потім виразити 𝑢𝑗(𝑡) і записати у відповіді оптимальні функції управління  та функції змінних стану  . Побудувати графіки функцій  .Зміст звіту про лабораторну роботу 1. Титульний лист: оформляється відповідно до додатка (текст, виділений курсивом, замінити відповідно до даних своєї роботи). 2. Завдання: сформулювати завдання та навести вихідні дані відповідно до варіанту. 3. Рішення: привести всі розрахункові формули, перетворення та проміжні результати. Усі формули мають бути забезпечені коментарями. У разі використання програми Matlab для виконання певної дії, наприклад, рішення рівняння, допускається наводити тільки систему рівняння та корені системи рівнянь, вказавши команду або номер рядка програми, в якій ця дія виконується. 4. Текст програми: вставити текст програми Matlab або іншої, яка використовувалась під час виконання лабораторної роботи. У тексті програми мають бути коментарі, які пояснюють, які дії виконуються на кожній ділянці коду. 5. Результати: у відповіді навести функції  та графіки цих функцій.Лабораторна робота №3. МЕТОД ЕЙЛЕРА-ЛАГРАНЖА: ЗАДАЧА З ФІКСОВАНИМИ КІНЦЯМИ Завдання Розв'яжіть задачу оптимального управління: перевести об'єкт управління, рівняння руху якого задані, в задане положення при мінімальній витраті енергії впливу управління. Початковий час 𝑡0 = 0. Рівняння руху, граничні умови і кінцевий час 𝑡𝑓 задані в табл. 1 за варіантами. Побудуйте графіки  та графік функції управління  Таблиця1 Вихідні дані до лабораторної роботи № 3  Закінчення табл. 1 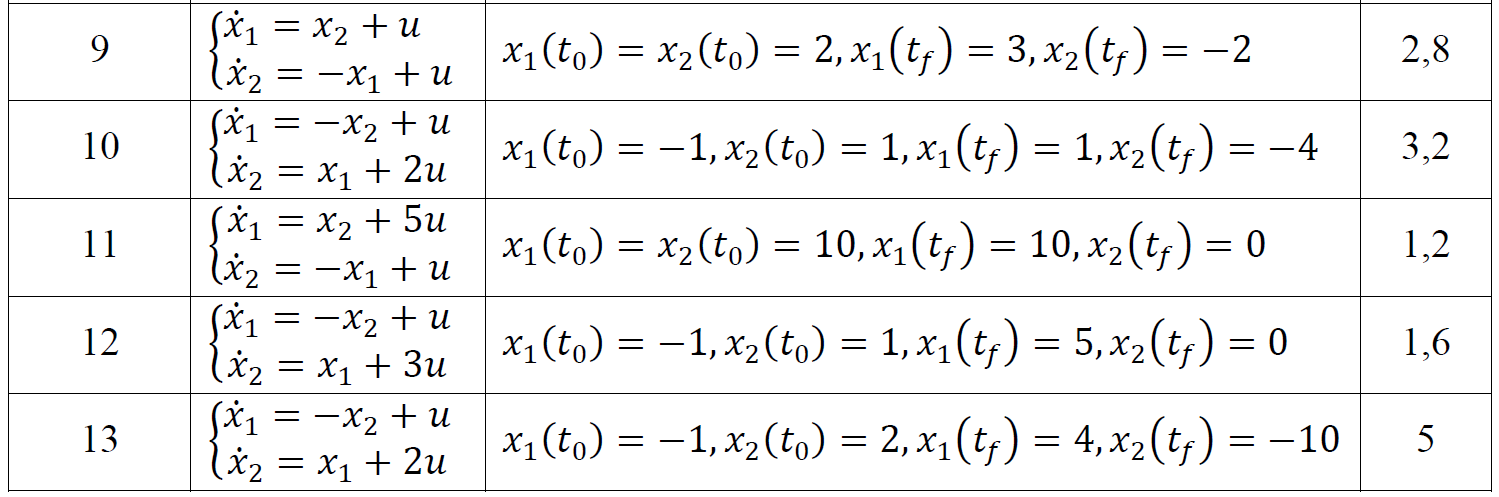 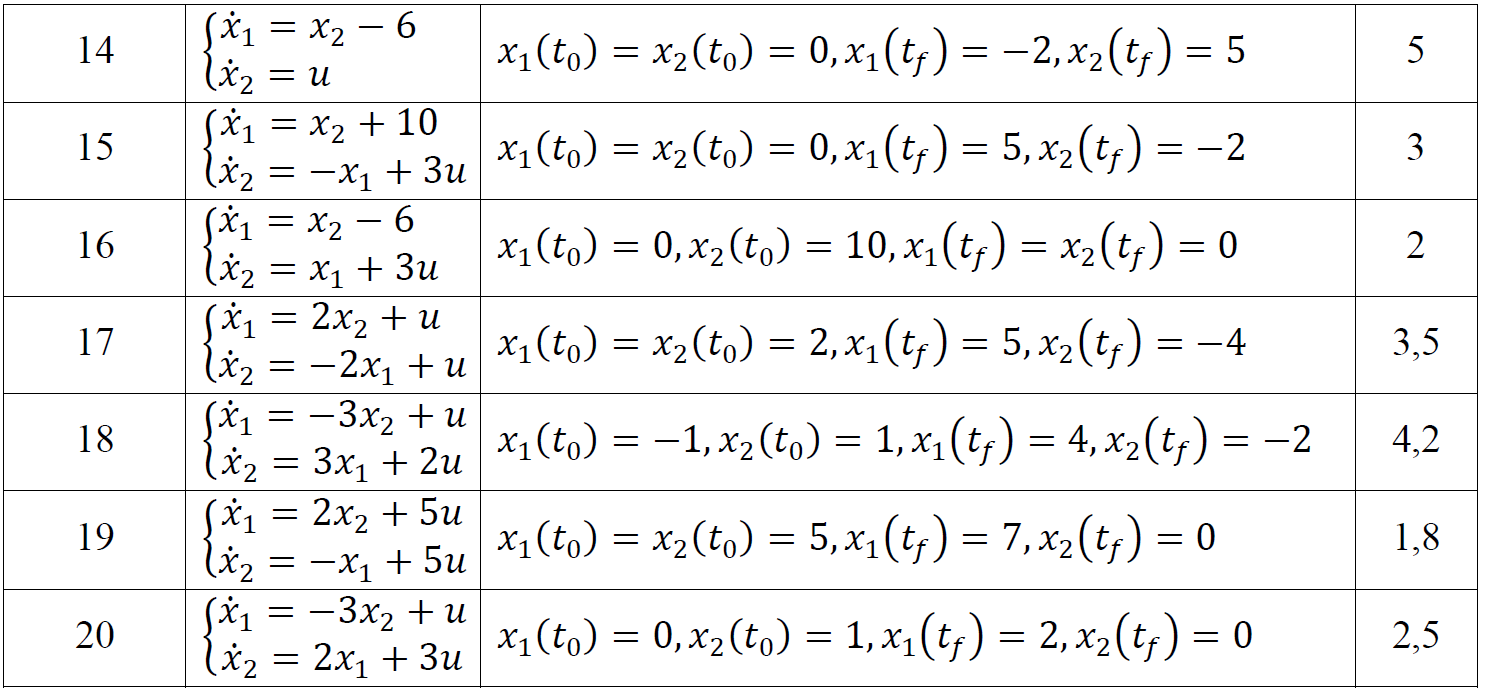 Приклад виконання лабораторної роботи №3 Вихідні дані: 1)Рівняння руху:  2) Граничні умови:  3) Критерій оптимальності у разі мінімальної витрати енергії керуючого впливу дорівнює: 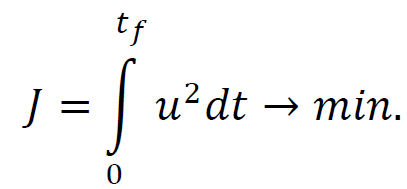 Рішення: Гамільтоніан 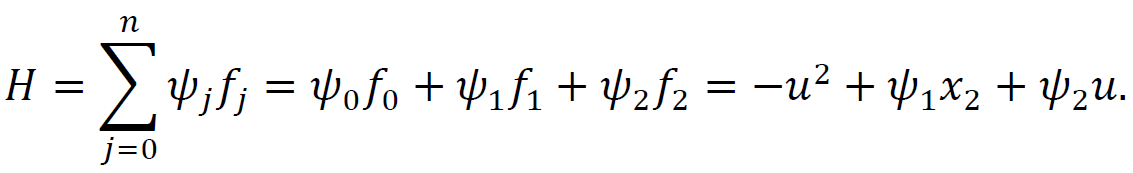 Рівняння Ейлера-Лагранжа 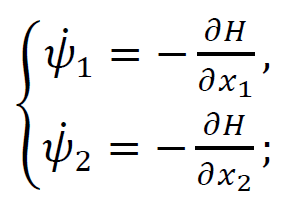 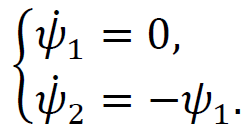 Умова стаціонарності  3) З умови стаціонарності висловимо 𝑢 = 𝜓2⁄2. Підставивши 𝑢 у рівняння руху та рівняння Ейлера-Лагранжа, отримаємо систему рівнянь 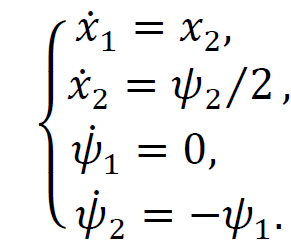 4) Вирішення даної системи диференціальних рівнянь має вид: 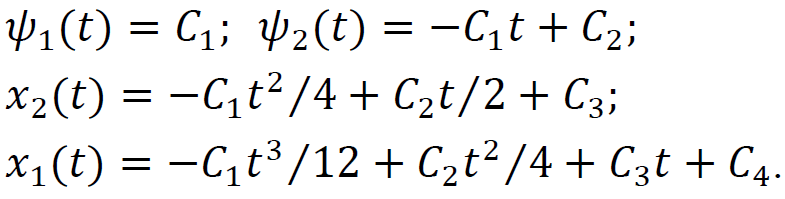 Дане рішення містить чотири постійних інтегрування: 𝐶1, 𝐶2, 𝐶3, 𝐶4, які можна знайти, використовуючи граничні умови: 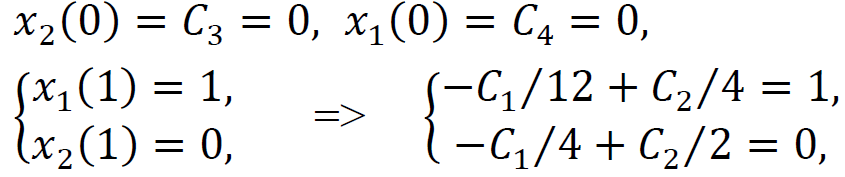 звідки  5) Підставивши знайдені постійні вирази для 𝑥𝑖(𝑡) і 𝜓𝑖(𝑡), отримаємо 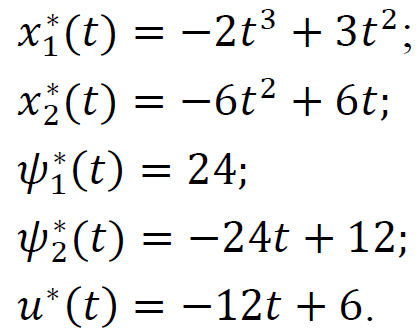 Графіки функції управління 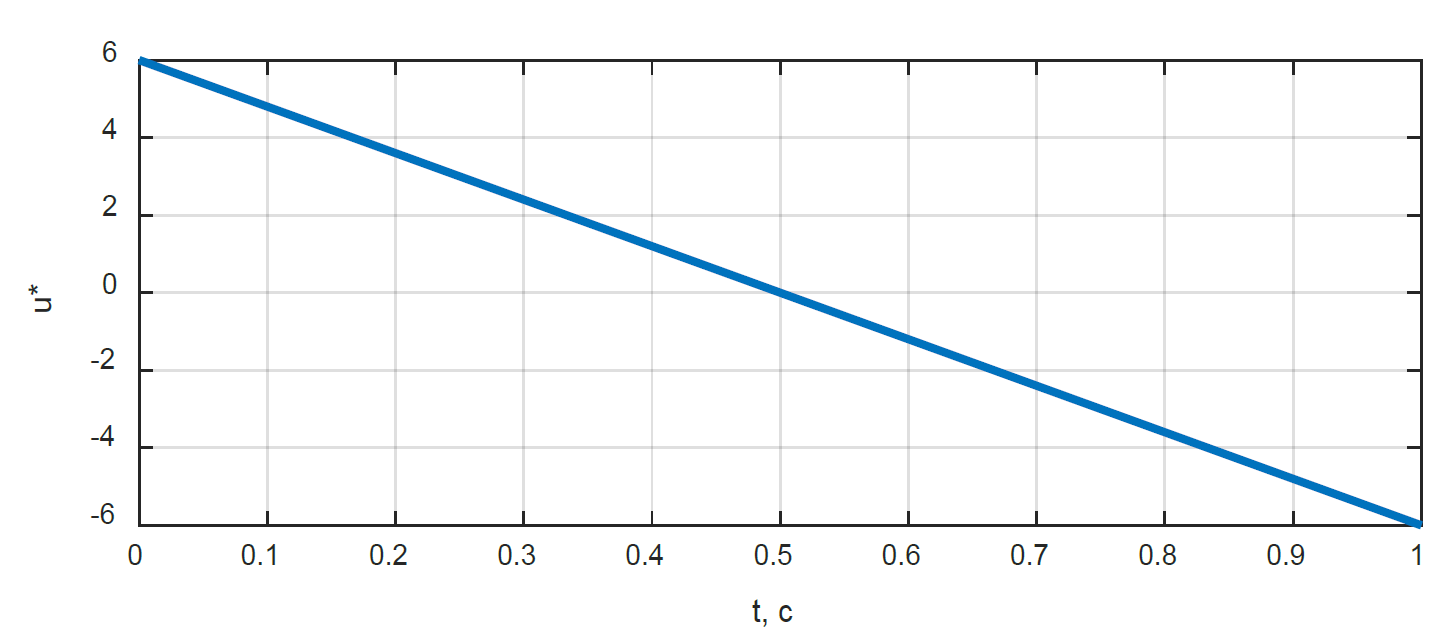 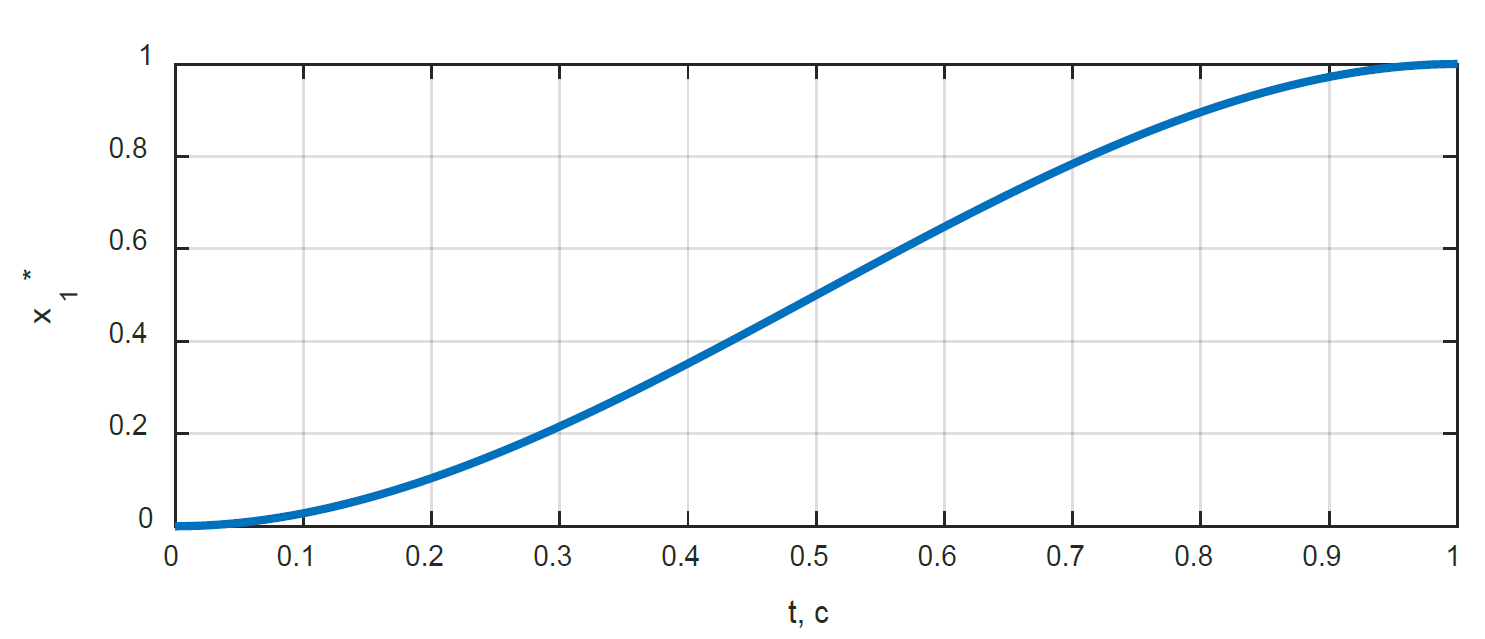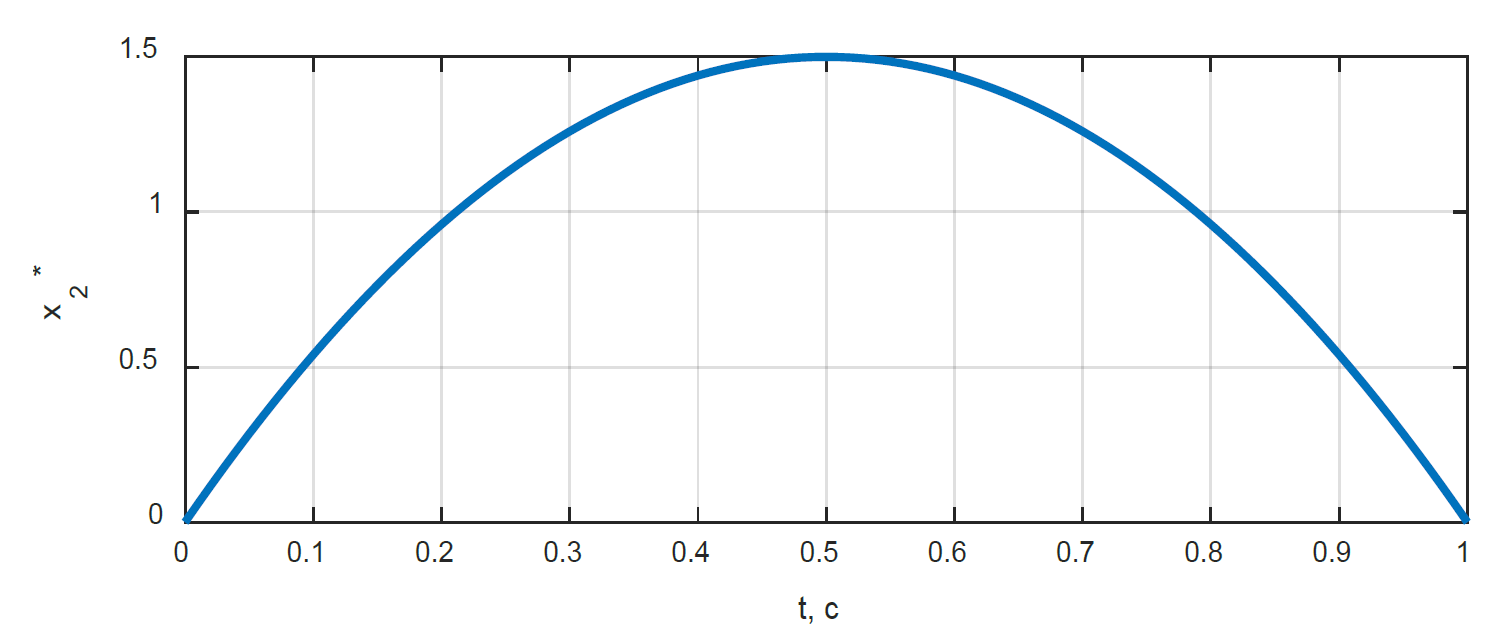та змінних стану  представлені на рис. 1.    Рис. 1. Залежність управління  та змінних стану  від часу Контрольні питання до лабораторної роботи №3 1. Розкажіть алгоритм розв'язання задачі оптимального керування за допомогою методу множників Лагранжа. 2. Як називаються величини 𝑥1, 𝑥2, 𝑢, 𝐶1, 𝐶2? 3. Як визначаються функції 𝑓0, 𝑓1, 𝑓2? 4. Чому дорівнює критерій оптимальності завдання? Як записати критерій оптимальності, виходячи з умов задачі? 5. Класифікуйте завдання, яке вирішується в лабораторній роботі. 6. Напишіть загальну формулу гамільтоніану. Як називаються величини 𝜓𝑖, 𝜆𝑘? 7. Як складаються рівняння Ейлера-Лагранжа? Для чого використовуються ці рівняння? 8. Як складається умова стаціонарності? Для чого вона використовується? 9. Що таке фазові змінні? 10. Що таке управляючі змінні? 11. Як визначаються постійні інтегрування?  |