Теориялы блім рiс деп рбiр нктесiне белгілі бір физикалы шама сйкес келетiн кеiстiктi бiр блiгiн айтамыз
 Скачать 73.51 Kb. Скачать 73.51 Kb.
|
|
1 – Зертханалық жұмыс Тақырыбы: . Скалярлы өріс және оның туындысы. Мақсаты:Студенттерді скалярлы өрістің дифференциалды сипаттамаларымен таныстырып, оны есептеу жолдарын көрсету, скалярлы өріс теңдеулерін шешу. Теориялық бөлім Өрiс деп әрбiр нүктесiне белгілі бір физикалық шама сәйкес келетiн кеңiстiктiң бiр бөлiгiн айтамыз. Физикалық шамалар скалярлы, векторлы және тензорлы болуына байланысты өрістер де скалярлы, векторлы,тензорлы болып келеді. Бұл өрістердің кез келгені тұрақты немесе айнымалы бола алады, егер ондағы физикалық шамалар уақыт бойынша өзгермейтін немесе олардың мәні уақыт бойынша өзгеретін болса. Скалярлық өріс деп әрбiр нүктесiне белгілі бір скалярлы физикалық шама сәйкес келетiн кеңiстiктiң бiр бөлiгiн айтамыз. Кеістіктіњ кез келген М н‰ктесі декартты координаталар системасында х,у,z координатасы арќылы немесе 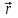 радиус векторы арќылы сипатталады: радиус векторы арќылы сипатталады: 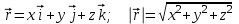 . .Осыѓан орай, скалярлы µріс тењдеуі координатадан функция ретінде 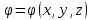 немесе радиус вектордан функция ретінде немесе радиус вектордан функция ретінде 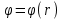 жазылады. жазылады.Б±л µрісте скаляарлы шама бір н‰ктеден екінші н‰ктеге µзгеріп отырады, яѓни скалярлы функция координатаѓа тєуелді. Сондыќтан функцияныњ кез келген н‰ктеніњ мањындаѓы µзгеру жылдамдыѓына функцияныњ туындысын қарастырамыз. Бірақ деңгейлік бет деген ұғымды скалярлық функцияның мәні кез келген нүктесінде бірдей мәнге ие болатын бет ретінде енгізетін болсақ, онда дењгейлік беттіњ кез –келген н‰ктесінен кез келген баѓытта алынѓан туынды - деңгейлік бетке нормаль баѓытта алынѓан туындыдан кем болады. Сондықтан скалярлы µрістіњ µзгеру жылдамдыѓын µрнектеу ‰шін дењгейлік бетке нормаль баѓыттаѓы туындыны ќарастырамыз. Ол ‰шін градиент деген ±ѓым енгіземіз. Скалярлы µрістіњ градиенті ретінде дењгейлік бетке нормаль баѓытталѓан векторды аламыз. Вектордыњ сандыќ мєні функцияныњ осы баѓыттаѓы туындысыныњ шамасына тењ, яѓни: 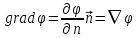 (1). (1).Вектордыњ баѓыты функцияныњ µсу баѓытымен сєйкес келеді, сондыќтан дењгейлік беттердіњ ењ биік ќабаттарын кµрсетеді. Градиент векторлыќ шама болѓандыќтан, оныњ кез келген баѓытта проекциясы болады, декартты координаталар системасында градиенттіњ проекциялары функцияныњ сол баѓыттаѓы туындысы арќылы аныќталады:  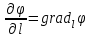 немесе немесе 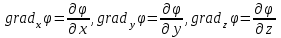 . .Градиент векторын оның проекциялары арќылы былай жазуѓа болады: 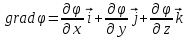 , (2) , (2)м±ндаѓы: 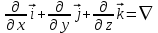 - Гамильтон операторы деп аталынады; - Гамильтон операторы деп аталынады; 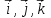 - осьтердегі бірлік векторлар. - осьтердегі бірлік векторлар.Градиент векторыныњ ұзындыѓы – вектордың модулі арќылы аныќталады: 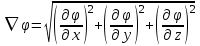 (3). (3).Сонымен скалярлы µрістіњ дењгейлік бетке нормаль бойынша туындысы векторлы µріс тудырады, ол сол µрістіњ дифференциалды сипаттамасы болып есептелінеді. Тапсырма: Вариантқа сай ( 1 Кесте, бөлім ) скалярлы өріс градиентін анықта ( тура есеп ). Градиент векторының ұзындығын анықта. Вариантқа сай ( 1Кесте) скалярлы өріс градиенті берілсе, өріс теңдеуін анықта ( кері есеп ). Кесте 1
Бақылау сұрақтары: ¤ріс аныќтамасы, оныњ т‰рлері. Скалярлы функцияныњ µзгеріс жылдамдыѓыныњ аныќталуы. Скалярлы функцияныњ градиенті дегеніміз не? Деңгейлік бет дегеніміз не? Градиенттің абсолютті шамасы қалай анықталады? Гамильтон операторының жазылымы қалай? |

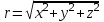 ;
;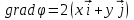
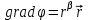 ,
,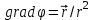 ,
,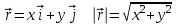
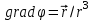 ,
,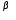 ,
, 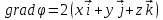
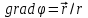 ,
,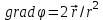 ,
,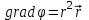
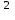
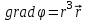
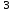
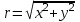 ;
;