Тепловой расчет цикла ГТУ. Тепловой расчет цикла гту с подводом тепла при p const

• Название: Тепловой расчет цикла гту с подводом тепла при p const
• Анкор: Тепловой расчет цикла ГТУ
• Дата: 08.12.2020
• Размер: 1.06 Mb.
• Имя файла: Тепловой расчет цикла ГТУ.odt
• Тип: Курсовая; #158099

Курсовая работа
по дисциплине: «Термодинамика»
на тему: «Тепловой расчет цикла ГТУ с подводом тепла при p = const»

Содержание

1. Задание на курсовую работу………………………………………………………...3

1.1 Аннотация…………………………………………………………………....4

1.2 Введение……………………………………………………………………...5

2. Теоретическая часть…………………………………………………………….....5-6

3. Практическая часть……………………………………………………………....6-14

3.1 Расчет идеального термодинамического цикла ГТУ……………....…...6-7

3.2 Определение коэффициента избытка воздуха…………………………8-13

3.3 Построение графиков..........................………………………………....14-15

4. Заключение……………………………………………………………………...…..16

5. Литература……………………………………………………………………...…...17

1. 
   Задание на курсовую работу по циклам ГТУ
   

Провести тепловой расчет цикла газотурбинной установки. Для проведения расчета заданы:

1) вид цикла – цикл Брайтона;

2) вид и свойства рабочего тела: воздух ( R= 287[Дж/кгК], Cp= 1004[Дж/кгК], Cv= 717[Дж/кгК], k= 1.4(показатель адиабаты), µ=28.97 [кг/кмоль]);

3) начальные параметры цикла: Pa= 100000[Па], Ta= 290[К];

4) степень повышения давления ; π=7

5) температура в конце сгорания Tz= 1573.15[К].

В тепловом расчете необходимо определить:

1) параметры газа в узловых точках (a, c, e, z);

2) удельные массовые теплоты q1 и q2 ;

3) работу компрессора Lк и турбины Lт;

4) работу L и термический коэффициент полезного действия (КПД) цикла в целом;

5. 
   построить p-v диаграмму цикла.
   

1. 
   Аннотация
   

В данной работе проводится тепловой расчет цикла газотурбинной установки (ГТУ) с учетом следующих допущений:

а) рабочий процесс является замкнутым;

б) рабочее тело (РТ) – идеальный газ с постоянной теплоемкостью;

в) подвод/отвод тепла осуществляется без изменения состава РТ;

г) механические, гидравлические, тепловые потери отсутствуют.

2. 
   Введение
   

Ввиду постоянного стремления ученых и инженеров повысить эффективность получения энергии важной проблемой остается преобразование тепловой энергии в механическую при минимальных затратах подводимой энергии к рабочему телу. На выходе из газотурбинной установки температура газов остается относительно высокой, что приводит к снижению общего термического КПД энергоустановки. В настоящей работе основной целью является определение КПД для ГТУ при заданных начальных данных (, ) и известной температуре продуктов сгорания на выходе из турбины .

2. 
   Теоретическая часть
   

ГТУ является разновидностью теплового двигателя, назначение которого состоит в преобразовании энергии в форме тепла в механическую энергию, отводимую в форме работы.

ГТУ работает следующим образом: воздух из окружающей среды поступает в компрессор К, в котором происходит адиабатное сжатие ( – повышаются). Из компрессора сжатый воздух поступает в камеру сгорания КС, в которую также при помощи насоса подается топливо. Затем происходит воспламенение смеси воздуха и топлива и протекает процесс горения при постоянном давлении ( - увеличиваются). Газообразные продукты сгорания поступают в турбину Т, в которой происходит их адиабатное расширение ( – понижаются, – увеличивается). В турбине осуществляется процесс преобразования кинетической энергии продуктов сгорания в механическую энергию вращения вала (например, электрогенератор). Из турбины отработанные продукты сгорания выбрасываются в атмосферу и охлаждаются до первоначальной температуры.

В основе работы ГТУ лежат идеальные термодинамические циклы – цикл Брайтона (подвод тепла при постоянном давлении), но с учетом некоторых допущений (описано выше). Общая схема ГТУ и вид термодинамического цикла в координатах представлены на Рис. 1 и Рис. 2 (см. Приложение).

3. 
   Практическая часть
   

3.1 Расчет идеального термодинамического цикла ГТУ

С учетом исходных данных начнем расчет цикла с определения параметров рабочего тела в точке a, воспользовавшись уравнением состояния для идеального газа:





Далее определим неизвестные параметры для узла c с учетом уравнения адиабатного процесса: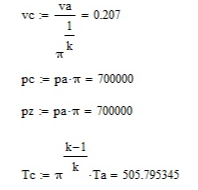


,

Аналогично для узла z получим следующее значение для удельного объема:





Теперь можем определить степень изобарного расширения как:




Наконец для узла e: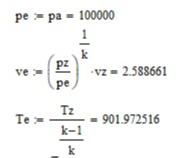





Вычислим удельные теплоты и :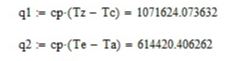





Работа компрессора и турбины соответственно равны: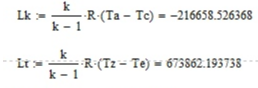





Отсюда следует, что работа цикла в целом равна сумме работ турбины и компрессора:






Откуда термический КПД цикла ГТУ равен:

.

3.2 Определение коэффициента избытка воздуха

Исходные данные:

1. 
   Топливо: Керосин Т-1;
   
2. 
   Массовый состав компонентов, %: C(0,860), H(0,140), O_Т(0);
   
3. 
   Теплота сгорания: Hu=43000 [кДж/кг];
   
4. 
   Среднемолекулярная масса: 140-160 [кг/кмоль].
   

Далее определим среднюю теплоемкость для продуктов сгорания (при условии полного сгорания. Учтем, что: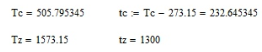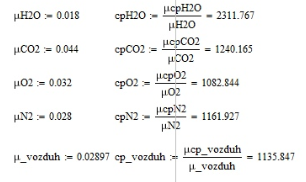




,

1. 
   С учетом ранее выбранного начального приближения для коэффициента избытка воздуха рассчитаем массовые и мольные доли продуктов сгорания: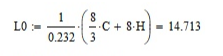
   

,
А масса горючего соответственно равна:





Тогда при подстановке данных в формулу получим, что:





Аналогично рассчитываем массовые доли других компонентов: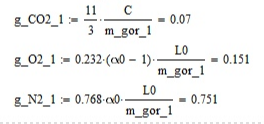





.

Теперь рассчитаем мольные и массовые удельные теплоемкости смеси в целом:


.

Далее, пересчитаем коэффициент :


,

Относительная ошибка (в %) равна: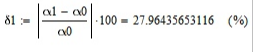





Вторая итерация:





Уточняем массовые и мольные составы продуктов сгорания с учетом того, что: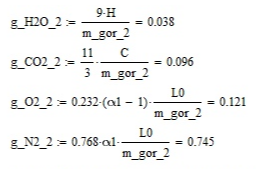






.

Уточним значение удельной массовой теплоемкости :



Снова пересчитываем коэффициент :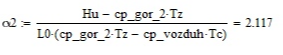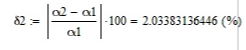




Третья итерация: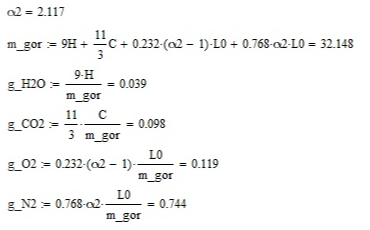

Уточним значение удельной массовой теплоемкости :



Снова пересчитываем коэффициент :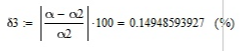





Так как значения последних двух полученных коэффициентов совпали с точностью до сотых, то процесс итераций останавливается.




Находим газовую постоянную для продуктов сгорания:



Пересчитаем удельные объемы для участка адиабатного расширения:



Используя уравнение для коэффициента адиабаты, а также закон Майера, вычислим коэффициент адиабаты для продуктов сгорания:


.

Отсюда новый удельный объем для точки e равен: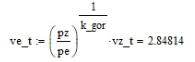





Далее уточним количество подведенного и отведенного тепла и найдем работу цикла: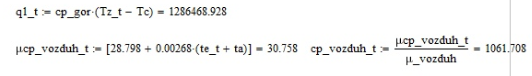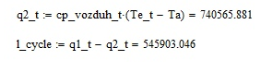




Откуда следует значение для КПД с учетом полученных поправок:



.

Энтропия идеального цикла: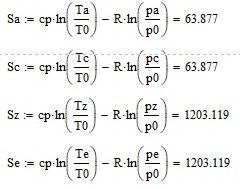


Энтропия теоретического цикла: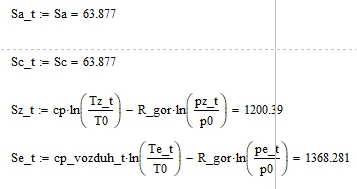





График p-V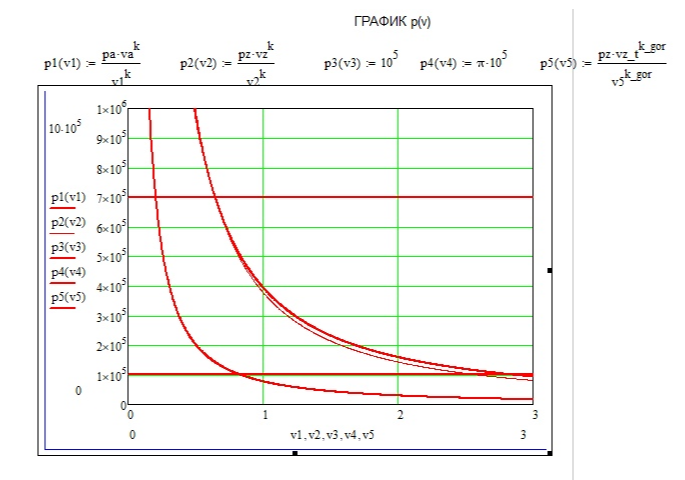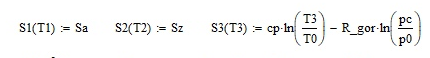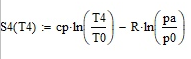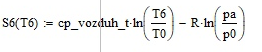









График T-S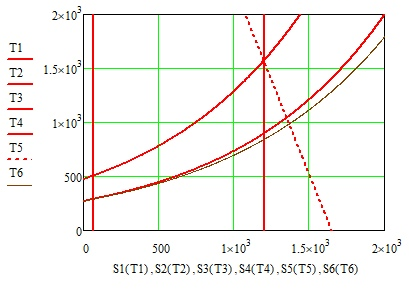

4. 
   Заключение
   

В данной работе при данных начальных условиях были получены значения КПД и составлен идеальный термодинамический цикл Брайтона с учетом некоторых допущений. Отметим, что значение КПД является достаточно высоким для тепловых машин. Итерационно было получено значение для коэффициента избытка воздуха, относительная погрешность на третьей итерации равняется меньше процента. По уравнениям (21)-(26), с учетом пересчета, определены массовые доли компонентов, а также удельные теплоемкости для продуктов сгорания и воздуха при постоянном давлении. С использованием первого, второго законов а также объединенного термодинамического тождества были построены графики идеального и теоретического термодинамических циклов.

5. 
   Литература
   

1. 
   Голдобеев В. И. Методические указания к курсовой работе по термодинамике: учеб. пособие / В. И. Голдобеев, С. Н. Арсланова. – Изд. Каз. Гос. Техн. Ун-та, 2001.
   
2. 
   ГОСТ 2.105-95 ЕСКД. Общие требования к текстовым документам./ Межгосударственный совет по метрологии, стандартизации и сертификации. – Минск: ИПК издательство стандартов, 1995.