Заказ №44 Термодинамический цикл 5 (Вариант 07). Термодинамический цикл 5

Название	Термодинамический цикл 5
Дата	04.05.2022
Размер	0.88 Mb.
Формат файла
Имя файла	Заказ №44 Термодинамический цикл 5 (Вариант 07).doc
Тип	Документы #511213

Термодинамический цикл 5

Вариант			Адиабата		Изотерма
		Изобара		Политропа		Изохора
		1	2	3	4	5	1
7	P	96000				275000	96000	2
	V		1,58
	T			1215	2220
Показатель политропы: 10

Дано:

=0,35

=0,5
Совершает цикл. Известны параметры:
Р₁= 96·10³ Па

Р₅ =2,75·10⁵ Па

T₃=1215 °С

T₄ =2220 °C

V₂ =1,58

n=10
Определить:

1. Параметры в характерных точках цикла Р,υ , T.

2. Средние массовые теплоемкости в процессах цикла.

3. Термодинамическую l и потенциальную работу w, теплоту q, изменение внутренней энергии

, энтальп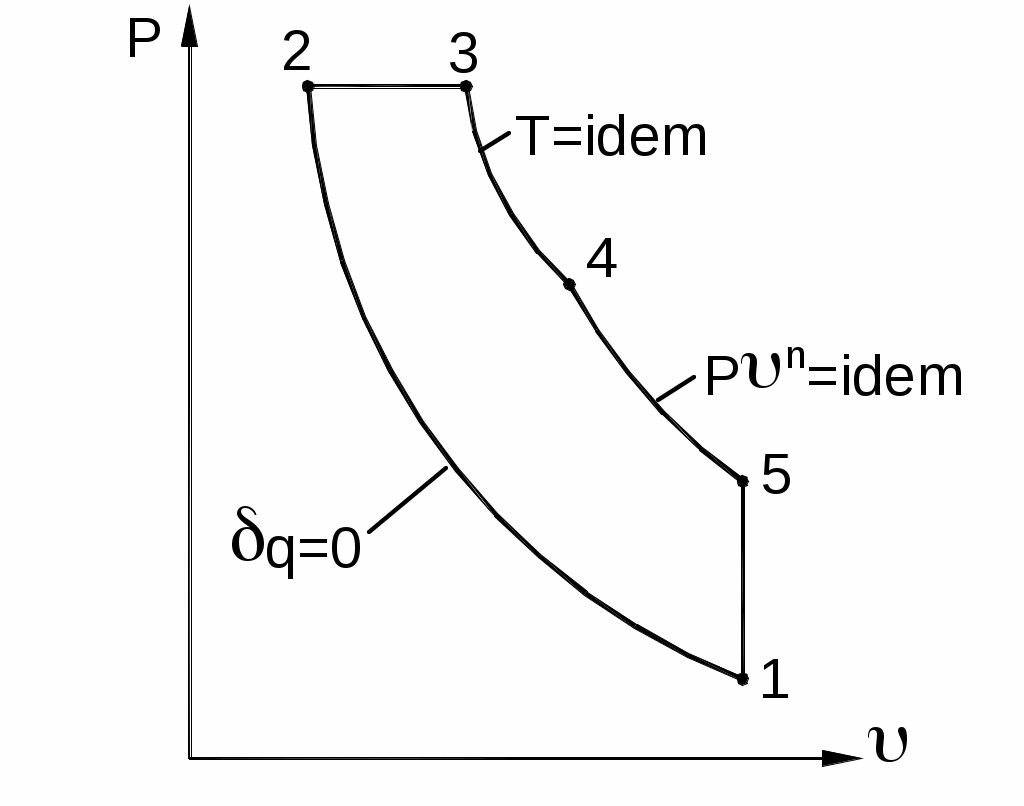ии

и энтропии

в процессах цикла, работу цикла

,термический к.п.д. цикла

.

Рисунок:

4. Построить цикл в координатах Р-V и Т -S.

Расчет газовой смеси (табл.1)

Состав газовых смесей

Компоненты смеси	CO₂	N₂	O₂	См№2
% содержание по объему	15	50	35
Молекулярная масса, μ	44	28,01	32

а) определение массового состава смеси: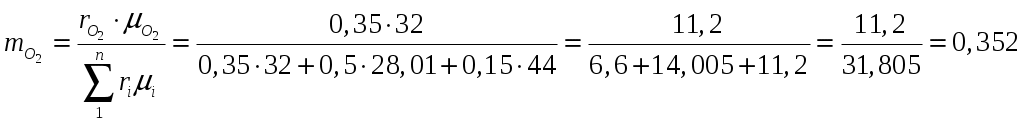

;

Проверка:

0,362 + 0,44 + 0,208 = 1.

б) определение кажущейся молярной массы смеси:

_см=

кг/К^.моль
Проверка: через объемные доли:

_см =

кг/К^.моль.
в) определение газовой постоянной смеси:

Дж/кг·К

R_i = 8314/

- газовая постоянная компонента.
Проверка: через объемные доли:

Дж/кг·К = 0,262 кДж/кг·К
РАСЧЕТ ПАРАМЕТРОВ:

Параметры состояния определяют по уравнению процесса, по соотношению между параметрами в процессах (табл.2), если в одной точке процесса известно три параметра, а в другой - один. Уравнение состояния – Клайперона применяют, если в точке известны два параметра из трех и для проверки.

1. p₂– по уравнению изобарного процесса 1-2, т.е.

р = idem; р₂ = р₁= 96·10³ Па.
2.

- из соотношения в адиабатном процессе 2 – 3:

, отсюда

Где:
k =

- показатель адиабаты.

Для определения

необходимо найти теплоемкости компонентов смеси в интервале от 0°С до t°C.

Таблица:

Диапазон температур	Теплоемкости, кДж/кг·К
Диапазон температур
0 - 580	0,99	1,074	1,035	0,73	0,777	0,846
0 - 1215	1,051	1,136	1,153	0,791	0,839	0,964

По формуле определяются средние массовые теплоемкости смеси в диапазоне температур от 0°С до 580°С и от 0°С до 1215°С, по формуле (2) - в диапазоне температур от 580°С до 1215°С.

кДж/кг·К;

кДж/кг·К.
Проверка по закону Майера:

R_см= 0,262 КДж/кг·К; 1,036 – 0,775 = 0,262

= 0,352·1,051 + 0,44·1,136 + 0,208·1,153 = 1,11 кДж/кг·К

= 0,352·0,791 + 0,44·0,839 + 0,208·0,964 = 0,848 кДж/кг·К
Проверка:

; 1,11 – 0,848 = 0,262 кДж/кг·К

кДж/кг·К

кДж/кг·К

Проверка: 1,177 – 0,915 = 0,262
Показатель адиабаты К = 1,177/0,915 = 1,3

м³/кг
3. p₃ - из соотношений адиабатического процесса 2 – 3:

= 66,57·10⁵ Па
Проверка по уравнению Клайперона:

= 66,57·10⁵ Па
4. По уравнению изотермического процесса 4 - 5:
T₄= T₅ = 2493 К
5.

– из соотношения параметров в изохорном процессе 5 – 1:
Р₅/Т₅= Р₁/Т₁

= 2493 · 96000 / 275000 = 870 °C
6.

определяется из уравнения Клайперона:

м³/кг
7. В изохорном процессе 5 – 1:

м³/кг
Проверка:

м³/кг
8. v₄ - из соотношения параметров для политропного процесса 3 – 4: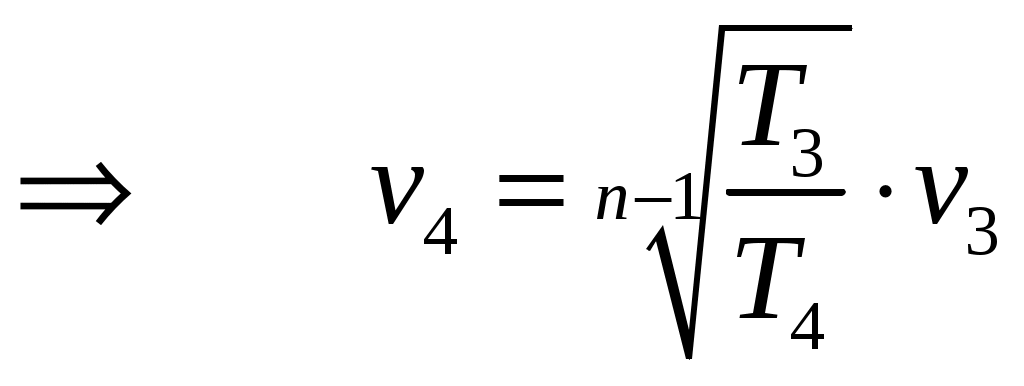

м³/кг
9. Р₄- тоже из соотношения параметров для политропного процесса 3 – 4: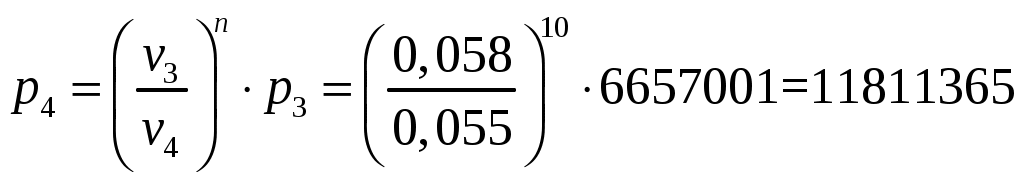

Па = 118,11·10⁵ Па
Проверка:

Па = 118,11·10⁵ Па
Или по уравнению изотермического процесса 4 - 5:

Па = 118,11·10⁵ Па

Вариант			Адиабата		Изотерма
		Изобара		Политропа		Изохора
		1	2	3	4	5	1
7	P	96000	96000	6657001	11811365	275000	96000	2
	V	2,37	1,58	0,058	0,055	2,37	2,37
	T	870	580	1488	2493	2493	870
Показатель политропы: 10

Результаты сводятся в табл. 3.

Таблица №3:

№ точек	p, Па	, м³/кг	T, К	t, ⁰С
1	0,96·10⁵	2,37	870	597
2	0,96·10⁵	1,58	580	307
3	66,57·10⁵	0,058	1488	1215
4	118,11·10⁵	0,055	2493	2220
5	2,75·10⁵	2,37	2493	2220

Средние массовые теплоемкости в процессах цикла

Расчет теплоемкостей в процессах цикла ведется аналогично расчету в адиабатном процессе 1-2.

Сначала определяются средние массовые теплоемкости компонентов смеси

в диапазоне от 0°С до температуры точек цикла по табл.8, 9 методом линейной интерполяции, обязательно проверяя расчет по закону Майера.

Например, для кислорода – в интервале температур от 0°С до 873 °С:

кДж/кг·К
0,993 – 0,733 = 0,260

кДж/кг·К
1,076 – 0,779 = 0,297

кДж/кг·К
1,04 – 0,851 = 0,189
После проверки результаты расчета сводятся в табл. 4.
Таблица №4:

Диапазон температур	Теплоемкости, кДж/кг·К
Диапазон температур
0 – 597	0,993	1,076	1,04	0,733	0,779	0,851
0 – 307	0,950	1,049	0,949	0,690	0,752	0,760
	0,260
	0,297
	0,189

Затем рассчитываются средние массовые теплоемкости смеси от 0°С до температур точек цикла по формуле (расчет обязательно проверяется по закону Майера).
Таблица №5:

0°C-t°C	0-580	0-1215	0-597	0-307
, кДж/кг·К	1,036	1,110	1,039	0,993
, кДж/кг·К	0,775	0,848	0,778	0,732
Проверка	0,262	0,262	0,262	0,262

Средние массовые теплоемкости смеси в процессах цикла рассчитываются по формуле (2). Для изотермического процесса 4-5.

= 0,352·1,051 + 0,44·1,136 + 0,208·1,153 = 1,11 кДж/кг·К

= 0,352·0,791 + 0,44·0,839 + 0,208·0,964 = 0,848 кДж/кг·К

Т.к. изменение температуры равно нулю. Проверив расчет теплоемкости по закону Майера, результаты сводят в табл. 6.

Таблица №6:

Процесс	1-2	2-3	3-4	5-1
Диапазон температур	597-307	307-1215	1215-2220	2220-597
,кДж/кг·К	1,088	1,177	1,262	1,230
, кДж/кг·К	0,826	0,915	1,000	0,968
Проверка	0,262	0,262	0,262	0,262

Термодинамическая работа l, потенциальная работа w, изменение внутренней энергии

u, изменение энтальпии

h, изменение энтропии

S , количество тепла q в процессах цикла.

Процесс 2-3, адиабатный:
k = 1,3

q = 0

=0,915(1488 – 580) = 830,82 кДж/кг

= l,177 (1488 – 580) = 1068,72 кДж/кг

кДж/кг

w ₂₃

кДж/кг

q₂₃= 0

dS =

q/T = 0

S₂₃= 0
Следовательно:
S₂ = S₃
Остальные процессы цикла рассчитываются аналогично, используя формулы табл.2.

Изобарный :

_{Изотермический}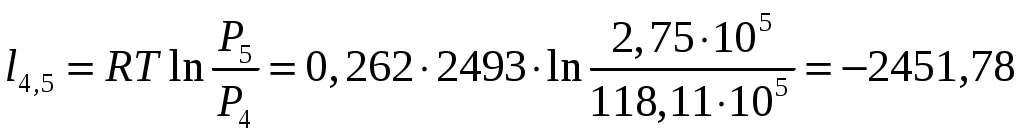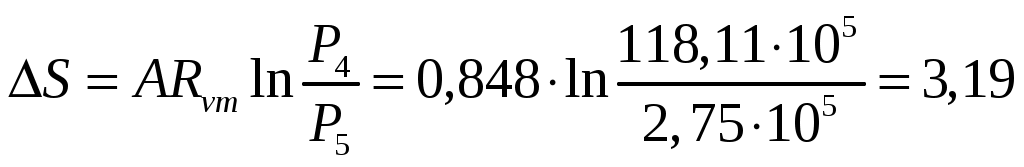

_{Изохорный}

_{Политропный}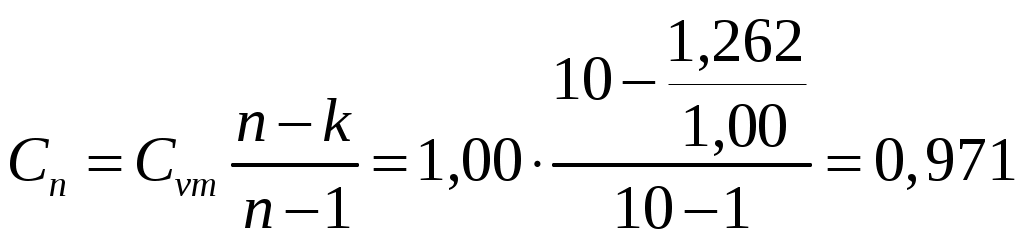

Результаты расчетов сведены в табл. 7:

Процесс	u кДж/кг	h кДж/кг	w кДж/кг	l кДж/кг	q кДж/кг	S кДж/кг·К
1-2	-239,54	-315,52	0	-75,98	-315,52	-0,441
2-3	830,82	1068,72	-1030,88	-792,987	0	0
3-4	1005	1268,31	-292,6	-29,26	975,86	0,501
4-5	0	0	-2451,78	-2451,78	-2451,78	3,19
5-1	-1571,064	-1996,29	425,23	0	-1571,064	-1,019
Показатели цикла	25,216	= 25,22	-3350,03	-3350,01	-3362,5	2,231

Термический к.п.д. цикла: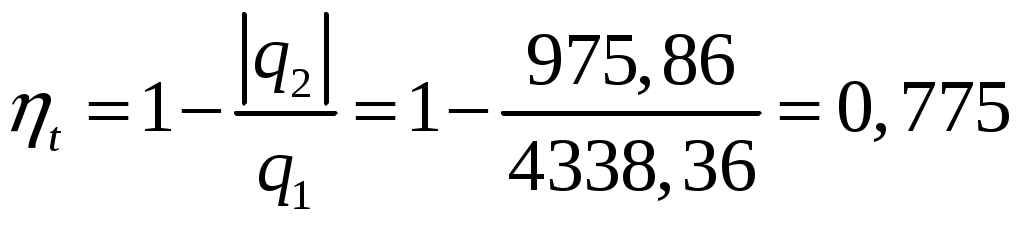

q₂ = q₄₅ + q₅₁ + q₁₂= –2451,78–1571,064 – 315,52= – 4338,36 кДж/кг

q₁ = q₃₄ =975,86 кДж/кг

l_ц=q₁ –

= 4338,36 – 975,86 = 3362,5 кДж/кг
Построение цикла в Р -V и Т -S координатах:

При изображении цикла в координатах Р-V (рис.2) сначала строятся характерные точки цикла (1, 2, 3, 4, 5) по известным значениям давления и удельного объема. Затем - процессы, изображаемые прямыми линиями - изобарический процесс 1- 2 и изохорический процесс 5-1. Для построения криволинейных процессов – адиабатического 2-3, изотермического 4 - 5 и политропного 3 - 4 - необходимо определить две-три промежуточные точки между характерными точками по уравнению процесса:
pV^k = idem

pV = idem

pVⁿ = idem

При построении цикла в координатах Т -S (рис.3) также сначала строятся характерные точки цикла по значениям T и

. Так как абсолютное значение энтропии неизвестно ни для одной из точек, то энтропия

выбирается произвольно, затем строятся процессы, изображаемые прямыми линиями - изотермический и адиабатный. При построении промежуточных точек криволинейных процессов температуры этих точек задаются, а изменение энтропии определяется по формулам (табл.2). Используя данные расчета характерных и промежуточных точек, термодинамический цикл изображается в масштабе в Р -V и Т -S координатах на миллиметровой бумаге (формат А4), (рис.2, 3)

(S₁ выбираем произвольно):

Рис. 2 - Расчетный цикл в координатах T-S:

4

5

1

3

2

1

2

3

4

5

Рис. 3 - Расчетный цикл в координатах P-V:
Средняя массовая теплоемкость при постоянном давлении

в диапазоне температур от 0ºС до 1ºС, кДж/кг·К

газовый теплоемкость термодинамический