|
|
ТермоЭДС. Термоэлектродвижущая сила
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Саратовский государственный технический университет
имени Гагарина Ю.А.»
Отчёт
о лабораторной работе
«Термоэлектродвижущая сила»
Выполнили:
студенты группы бИФБС-11
Антонова К.А.
Могильницкая И.А.
Туралиева К.Б.
Лачина А.А.
Павлов Г.С.
Проверил:
Разуков Вадим Алексеевич
(дата, подпись)
Саратов 2021
Термоэлектродвижущая сила
Цель работы: изучение контактных явлений в металлах и термоэлектрических методов измерения температуры, снятие зависимости термоэлектродвижущей силы от разности температур холодного и горячего спаев, градуировка термопары, определение постоянной термопары и концентрации электронов.
Основные понятия.
Экспериментально доказано, что в металлах, имеются свободные электроны, способные перемещаться по металлу. Такая система свободных электронов в кристаллической решетке называется электронным газом. Свободными электроны в металле можно считать лишь относительно. Вблизи границы металла на электроны действует электрическая сила, удерживающая их внутри металла. Чтобы преодолеть эту силу, электрон должен совершить определенную работу. Для удобства количественного описания процесса необходимо ввести понятие «потенциального ящика». Можно полагать, что электроны внутри металла имеют определенную отрицательную энергию, которая резко возрастает и обращается в нуль на границе металла.
Электрон в металле имеет, таким образом, кинетическую εи потенциальную энергию еU. Полная энергия eU+εпри eUε отрицательна. Глубина «потенциального ящика» (т. е. величина eU) определяется параметрами металла и свойствами поверхности, а кинетическая энергия ε – температурой и уровнем Ферми.
Для того, чтобы вырвать электрон из металла, ему необходимо сообщить энергию (e), достаточную для преодоления потенциального барьера.
С увеличением температуры энергия электронов повышается. Однако, даже при температурах, близких к температуре плавления, глубина потенциального ящика остается практически неизменной, так что энергию, которую нужно сообщить электрону для вырывания его из металла, можно определить по той же формуле, что и при Т=0.
 e e
eU=W
εmax
Вследствие теплового движения электроны проводимости могут выходить из металла в окружающее пространство. В результате вылета электронов из металла вблизи поверхности проводника образуется двойной электрический слой толщиной величиной в несколько межатомных расстояний. Металл оказывается заряженным положительно, а вылетающие электроны образуют отрицательно заряженное «облако». Между металлом и электронным облаком возникает разность потенциалов . Для различных металлов колеблется от 1 до 10В и зависит как от химической природы металла, так и от состояния его поверхности. Электрон, выходя из металла, совершает работу против сил притяжения со стороны положительно заряженного проводника и против сил отталкивания со стороны ранее вылетевших электронов. Эта работа совершается за счет уменьшения кинетической энергии электронов и называется работой выхода электрона из данного металла. Работа выхода А=eU-εmaxсвязана с разностью потенциалов
=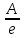 , где е – величина заряда электрона. , где е – величина заряда электрона.
При соприкосновении двух проводников электроны вследствие теплового движения переходят из одного проводника в другой. Если соприкасающиеся проводники различны или если их температуры в разных точках неодинаковы, то оба потока диффузии электронов неодинаковы и один из проводников заряжается положительно, а другой отрицательно. Поэтому в пограничном слое между проводниками появляется электрическое поле, уравновешивающее разность диффузных потоков. Опыт показывает, что в контакте двух различных проводников наблюдается тепловые явления при протекании электрического тока (в зависимости от направления тока проходит либо нагревание, либо охлаждение контакта). Это явление получило название явления Пельтье.
Наличие тепла Пельтье означает, что кинетическая энергия электронов при переходе из одного проводника в другой изменяется. Если она увеличивается, то спай нагревается, если же она уменьшается, то спай охлаждается. Это значит, что между обоими проводниками имеется некоторая разность потенциалов, которая не зависит от тока и существует даже в его отсутствии. Она получила название внутренней контактной разности потенциалов.
Возникновение внутренней контактной разности объясняется следующим образом. Рассмотрим два различных металла 1 и 2, находящихся при одной и той же температуре, и предположим, что мы привели их в соприкосновение. Электроны проводимости вследствие теплового движения будут переходить из проводника 1 в проводник 2 и обратно. Так как концентрация электронов в обоих металлах различна, то и диффузионные потоки электронов будут неодинаковыми. Положим, что концентрация электронов в металле 1 больше концентрации в металле 2. Тогда поток диффузии электронов из металла 1 будет больше потока диффузии в обратном направлении и металл 1 будет заражаться положительно, а металл 2 – отрицательно. В результате этого между металлами возникнет разность потенциалов и появится электрическое поле, которое вызовет дополнительное движение электронов (переносное или дрейфовое движение) в обратном направлении – от металла 2 к металлу 1, поэтому общее количество электронов, переходящих от 1 к 2, будет уменьшаться, а идущих в противоположном направлении – увеличиваться. При некоторой контактной внутренней разности потенциалов Uвнутр. между металлами установиться равновесие и потенциалы металлов не будут уже изменяться. Эта разность потенциалов и является внутренней контактной разностью потенциалов обоих металлов.
Отметим, что вследствие большой тепловой скорости электронов обмен электронами происходит весьма быстро и равновесие устанавливается уже в ничтожные доли секунды.
Согласно закону Ома, плотность тока внутри металла равна 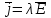 . Так как в равновесии j=0, то и электрическое поле в любой точке в толще металлов равно нулю. Это значит, что электрическое поле . Так как в равновесии j=0, то и электрическое поле в любой точке в толще металлов равно нулю. Это значит, что электрическое поле 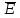 существует только в тонком пограничном слое между обоими проводниками, на котором сосредоточена и вся контактная разность потенциалов. существует только в тонком пограничном слое между обоими проводниками, на котором сосредоточена и вся контактная разность потенциалов.
Полученные результаты можно наглядно представить с помощью энергетической диаграммы.
 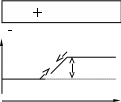
W
1 2
еU внутр
X
Будем откладывать по вертикальной оси потенциальную энергию электрона внутри металла, равную W=eU ( е – заряд электрона, U – значение потенциала), а по горизонтальной оси – перемещение вдоль металла. Тогда получиться распределение энергии, изображенное на рисунке.
Так как в отсутствии тока потенциал внутри металла одинаков, то и энергия W постоянна в различных точках одного и того же металла. Однако ее значение о обоих металлах различно и меньше в металле 1, зараженном положительно, нежели в проводнике 2 (т.к. заряд электрона е0). Разность энергии электрона в обоих проводниках равна eUвнутр.
Вычислим теперь величину внутренней контактной разности потенциалов.
В классической электронной теории задача о равновесии электронов в двух соприкасающихся проводниках не отличается от задачи о равновесии атомарного газа, находящегося в поле тяжести. Из молекулярной физики известно, что концентрация атомов газа n на высоте h связана с концентрацией n0 у поверхности земли формулой:
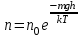 , где m – масса атома, g – ускорение поля тяжести, и k – постоянная Больцмана, T – абсолютная температура, которая предполагается одинаковой во всем газе. Здесь mgh есть разность потенциальных энергий (W1-W2) атома газа на высоте h и у поверхности земли. В случае двух соприкасающихся металлов W1-W2=eUвнутр и поэтому , где m – масса атома, g – ускорение поля тяжести, и k – постоянная Больцмана, T – абсолютная температура, которая предполагается одинаковой во всем газе. Здесь mgh есть разность потенциальных энергий (W1-W2) атома газа на высоте h и у поверхности земли. В случае двух соприкасающихся металлов W1-W2=eUвнутр и поэтому
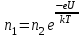 , где n1 и n2 – концентрации электронов в обоих металлах. Отсюда , где n1 и n2 – концентрации электронов в обоих металлах. Отсюда
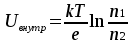
Полученная формула показывает, что чем больше различие в концентрациях электронов и, тем больше и внутренняя контактная разность.
     А Б А Б
0 e2 eUвнешн
e1 eUвнутр
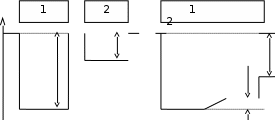
Возникновение внешней контактной разности потенциалов объясняется следующим образом. Рассмотрим, какое электрическое состояние установиться у свободных концов двух соприкасающихся металлов. Пусть, сначала два различных металла 1 и 2 разобщены друг с другом. В этом случае потенциальная энергия электрона в различных точках пространства изображаются кривыми. При построении этого графика энергия покоящегося электрона в вакууме (вне металла) принята равной нулю. Так как оба металла не заряжены, то электрического поля между ними нет и энергия электрона в пространстве между металлами остается постоянной. Она постоянна и внутри металлов (точнее, постоянно ее среднее значение), но имеет другую, меньшую величину. Каждый кусок металла на этом графике характеризуется потенциальным ящиком.
В классической теории глубина потенциальной ямы равна термоэлектронной работе выхода электрона из металла А.
Проведем теперь в соприкосновение оба куска металла. Тогда в контактном слое вследствие диффузии электронов установиться скачок потенциала U внутр, равный внутренней контактной разности потенциалов, и между днищами обоих потенциальных ящиков будет малое энергетическое расстояние eU. Но так как глубины потенциальных ящиков различны, то их внешние края окажутся на разных высотах. Это значит, что между двумя любыми точками А и Б, находящимися вне металлов, но расположенными в непосредственной близости от их поверхностей, возникает разность потенциалов. Она получила название внешней контактной разности потенциалов обоих металлов. Между обоими соприкасающимися металлами во внешнем пространстве появиться электрическое поле, а на поверхности металлов возникнут электрические заряды.
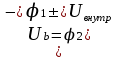 , где знак + или – следует выбирать в зависимости от знака внутренней контактной разности. , где знак + или – следует выбирать в зависимости от знака внутренней контактной разности.
Оценка показывает, что U внутр мало и имеет порядок 10-2–10-3 В. Напротив, работы выхода А измеряются несколькими эВ и такой же порядок имеет их разность для различных пар металлов. Поэтому с достаточной точностью можно считать:
Uв=(А2-А1)/e т.е. контактная разность потенциалов двух металлов равна разности их работ выхода. Квантовая теория металлов показывает, что формула верна абсолютно точно.
Рассмотрим теперь цепь, состоящую не из двух, а из нескольких металлов 1, 2, 3, 4. Если бы мы ее разрезали по аа, то между свободными концами металлов 1 и 2 была бы контактная разность
U12 = 2 - 1
Аналогично между разрезами аа и бб была бы разность потенциалов U23 = 3 - 2
а у последней пары металлов U34 = 4 - 3
Так как в плоскостях аа. бб и т. д. соприкасаются одинаковые металлы, то дополнительные разности потенциалов здесь не возникают, поэтому контактная разность всей цепи равна
U12+U23+U34=(v2-v1) +(v3-v2) +(v1-v3) =v4-v1=U14 (2.5)
т. е. такая же, как в отсутствии промежуточных металлов 2 и 3. Контактная разность определяется только крайними металлами цепи.
Если имеется замкнутая цепь, составленная из разных металлов или вообще из электронных проводников (проводников первого класса), то внешняя контактная разность вообще не возникает, и остаются только внутренние контактные разности и т. д.
Сумма этих скачков потенциала равна
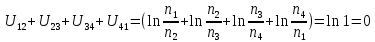
Следовательно, и электродвижущая сила цепи, составленной из каких угодно проводников первого класса, но находящихся при одинаковой температуре, равна нулю. Такой же результат получается и в квантовой теории металлов.
Составим замкнутую цепь из двух разнородных металлов и будем
поддерживать температуру контактов a и b (спаев) различными температурами Ta и Tb. Контактные разности потенциалов в спаях a и b различны по величине вследствие различной температуры спаев. Подсчитаем ЭДС

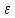 = =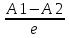 + +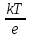 ln ln 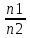 + +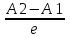 - -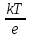 ln ln 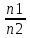 = =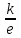 ln ln 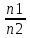 (Ta-Tb) (Ta-Tb)
Постоянная для двух данных металлов величина называется
α =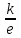 ln ln 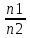
постоянной термопары или удельной термо-э.д.с. Формула для расчета ЭДС может быть записана следующим образом:
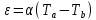
Методика эксперимента.
В установке используют термопарный термометр, состоящий из батареи последовательно соединенных холодных и горячих спаев двух разнородных металлов. Горячие спаи помещены в сосуд с водой, нагреваемый элементом. Температура воды регистрируется термометром. Холодные спаи помещены в сосуд с водой при комнатной температуре, регистрируемой термометром. Так как горячие и холодные спаи одинаковы, то по формуле для последовательного соединения М спаев перепишется так:
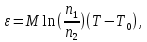
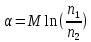
Где α – постоянная термопары.
При включении нагревателя температура горячих спаев увеличивается и по цепи с милливольтметром потечет ток. В процессе измерения регистрируется линейная зависимость термоэлектродвижущей силы от разности температур горячего и холодного спаев. Тангенс угла наклона 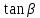 прямой V=f(T-T0) к оси абсцисс равен постоянной термопары а, то есть прямой V=f(T-T0) к оси абсцисс равен постоянной термопары а, то есть
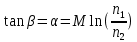
Откуда
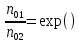
Порядок выполнения работы.
1.При включении нагревателя температура горячих спаев увеличивается и по цепи с милливольтметром течет ток.
T0 = 26 0C, где Т0 – температура холодных спаев (комнатная температура).
При увеличении температуры на каждые 40С будем снимать показания вольтметра. Построим таблицу:
                         
T 0 4 8 12 16 20 24 28 32 36 40 44 48 52 54
U 0 0,6 1,1 1,5 1,9 2,1 2,2 2,5 2,9 3,1 3,4 3,8 4,0 4,2 4,3
U

Uд=Uзн*10-3 B.
М=6, М – число спаев.

2. Построим зависимость термоэлектродвижущей силы от разности температур горячего и холодного спаев ( Т).
Через точки проведем прямую.
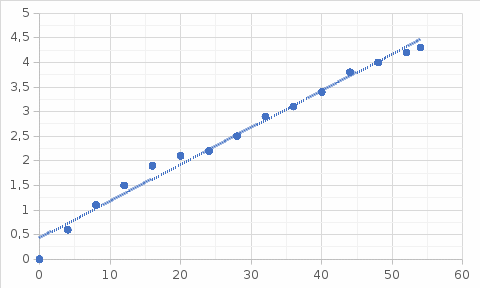
3. Вычисление постоянной термопары α по зависимости U=α(T-T0) и случайной погрешности осуществляется по методу наименьших квадратов. При этом уравнение линейной регрессии имеет вид:
Y = A*X,
Где А – угловой коэффициент наклона прямой, проходящей через начало координат. Этот коэффициент находится по формуле:
A =  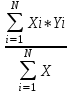  ,здесь X = ,здесь X = 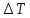 , Y = U, A = α. , Y = U, A = α.
Определим этот коэффициент, переводя температуру из цельсия в кельвины:
А = 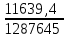 0,009 0,009
4. Определим отношение концентрации носителей по формуле:
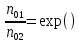
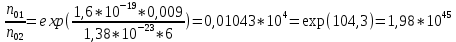
Расчет погрешностей.
1.Погрешность определения углового коэффициента 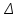 А находится из соотношения: А находится из соотношения:
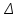 A = S A = S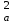 = =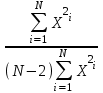 - - 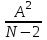
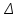 A = A = 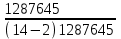 - - 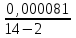 = 0,083 – 0,0000067=0,0829 = 8%. = 0,083 – 0,0000067=0,0829 = 8%.
Приборная погрешность определения α складывается из систематических погрешностей измерения термоэдс и температуры, и на основании зависимости α=V/(T-T0) вычисляется по формуле:
(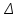 α)пр = α)пр = 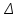 αпр αпр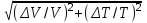 , ,
где 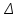 V/V – класс точности вольтметра, V/V – класс точности вольтметра, 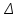 Т/Т –относительная погрешность измерения температуры. Величина Т/Т –относительная погрешность измерения температуры. Величина 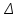 Т определяется по цене деления амперметра, пересчитанной в градусах. Т определяется по цене деления амперметра, пересчитанной в градусах.
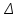 V/V = 0,025 V/V = 0,025
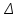 T/T = 0,01 T/T = 0,01
(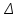 αпр) = 0,0002 αпр) = 0,0002
Суммирование систематической и случайной погрешностей осуществляется по формуле:
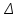 α= α=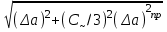
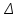 α= 0,02 α= 0,02
2.Рабочая формула для расчета отношения концентрации носителей:
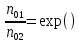
Расчет погрешности 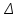 n осуществляется как расчет погрешности косвенного измерения, в результате чего получается формула: n осуществляется как расчет погрешности косвенного измерения, в результате чего получается формула:
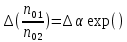
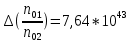
Вывод:
При помощи проведенных опытов изучил контактные явления в металлах. Построил зависимость термоэлектродвижущей силы от разности температур холодного и горячего спаев. Определил постоянную термопары:
A = 0,009 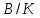
В результате измерений возникла погрешность равная:
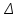 А = 8% А = 8%
Общая погрешность постоянной термопары (суммирование систематической и случайной погрешности) равна:
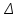 α = 0,02 α = 0,02
В ходе работы также определил отношение концентрации носителей:
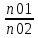 = 1,98*1045 = 1,98*1045 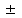 7,64*1043 7,64*1043
В ходе работы могла возникнуть небольшая погрешность из-за неточности приборов – термометра и вольтметра. |
|
|
 Скачать 143.82 Kb.
Скачать 143.82 Kb.