Алгебра. Сухарева ММ 2 Семестр самостоятельная работа по математике вариа. Тест 10. Степенная фуhkции

• Название: Тест 10. Степенная фуhkции
• Анкор: Алгебра
• Дата: 11.02.2023
• Размер: 25.63 Kb.
• Имя файла: Сухарева ММ 2 Семестр самостоятельная работа по математике вариа.docx
• Тип: Самостоятельная работа; #931608

Министерство образования и науки Российской Федерации
 

Частное учреждение профессионального образования
 «Высшая школа предпринимательства»
 (ЧУПО «ВШП»)

 

 

 

 

 

Самостоятельная работа.

по дисциплине

«Математика»
 

 

 

 

 

 

Выполнила:

Студентка 1 курса заочного отделения

специальности «Банковское дело»

Сухарева М.М.

 

 

 

 

 

 

 

 

 

 
Тверь, 2023

ТЕСТ 10. СТЕПЕННАЯ ФУHKЦИИ

Вариант 1

Часть 1

_{A1. Ответ} 2) (2; 16)
C самого начала следует отметить, что для того, чтобы проверить все предложенные точки на принадлежность их графику функции y = x ⁴, необходимо подставить вместо x и y координаты каждой точки и проверить, будет ли выполняться равенство.

A2. _Ответ 3) 1 и 2

A3.

Ответ №1

у (х)= 3х^4 + 2х^2

первая область определения симметрична относительно начала отсчета. и при замене аргумента х на -х значение функции не меняется. т.к. -х возводят в четную степень.

1)

у (х)= 3х^4 + 2х^2

у (-х)= 3(-х)^4 + 2(-х)^2

у (х) =у (-х)

^A4.

Ответ

3)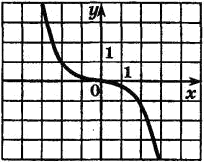

Чвсть 2

^B1.

F(-2)=(-2)^17-1<0
f(2)=2^17-1>1
f(1)=1^17-1=0
f(-2)132
B2. т.к. степень нечетная то решением будет одно число


Какая степень у переменной - столько будет и корней
в том числе и мнимых)
т.е. 1 действительное решение и 14 решений в тригонометрической форме с мнимыми частями

ВЗ. x3+27=0x3+27=0

Вычтем 2727 из обеих частей уравнения.

x3=−27x3=-27

Добавим 2727 к обеим частям уравнения.

x3+27=0x3+27=0

Разложим левую часть уравнения на множители.

(x+3)(x2−3x+9)=0(x+3)(x2-3x+9)=0

Если любой отдельный множитель в левой части уравнения равен 00, все выражение равно 00.

x+3=0x+3=0

x2−3x+9=0x2-3x+9=0

Приравняем x+3x+3 к 00, затем решим относительно xx.

x=−3x=-3

Приравняем x2−3x+9x2-3x+9 к 00, затем решим относительно xx.

x=3+3i√32,3−3i√32x=3+3i32,3-3i32

Окончательным решением являются все значения, при которых (x+3)(x2−3x+9)=0(x+3)(x2-3x+9)=0 верно.

x=−3,3+3i√32,3−3i√32
С1. НЕТ ОТВЕТА.