ОКTest_5_1. Тесты к экзамену по учебной дисциплине теоретическая механика для студентов специальностей

• Название: Тесты к экзамену по учебной дисциплине теоретическая механика для студентов специальностей
• Дата: 12.03.2023
• Размер: 0.58 Mb.
• Имя файла: ОКTest_5_1.doc
• Тип: Тесты; #981973
• страница: 3 из 4

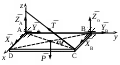436.

В условиях задачи 35 найти

1.

2.

3.

4.

5.

1

2

3

437.

В условиях задачи 35 найти

1.

2.

3.

4.

5.

38.

В условиях задачи 35 найти

1. ; 2.

3. ; 4.

5.

39.

Указать правильную формулу для определения центра тяжести тела С, если – веса частиц тела в точках с радиусами-векторами , – вес всего тела

1. ; 2. ;

3. ; 4. ;

5. .

40.

В кинематике изучают

1. Устойчивость различных движений твердого тела

2. Условия равновесия и движения твердого тела в разных случаях

3. Движение тел при учете действующих сил

4. Движение тел без учета причин, вызывающих эти движения, то есть действующих сил

5. Законы движения материальной точки и твердого тела при действии различных сил

41.

Движение материальной точки при векторном способе задания движения описывается следующим уравнением (уравнениями)

1. S = v t; 4. S = ;

2. S = S (t); 5. r =r (t).

3. x = x (t), y = y (t), z = z (t);

42.

Какими уравнениями определяется координатный способ задания движения?

1. S = v t; 4. S = ;

2. S = S (t); 5. r =r (t).

3. x = x (t), y = y (t), z = z (t);

43.

Каким уравнением описывается естественный способ задания движения материальной точки?

1. S = v t; 4. S = ;

2. S = S (t); 5. r =r (t).

3. x = x (t), y = y (t), z = z (t);

44.

При естественном способе помимо криволинейной координаты точки необходимо еще задать

1. 
   Траекторию точки, начало отсчета на ней, а также положительное и отрицательное направления отсчета
   
2. 
   Радиус-вектор точки
   
3. 
   Прямоугольные координаты точки, как функции времени
   
4. 
   Траекторию и вектор скорости точки
   
5. 
   Траекторию, скорость и ускорение точки
   

1

2

3

445.

Закон движения точки задан уравнением . Определить мгновенную скорость движения.

1. ; 2. ;

3. ; 4. ;

5.

446.

Как направлена мгновенная скорость точки?

1. 
   По касательной к траектории точки
   
2. 
   По внешней нормали к траектории
   
3. 
   По внутренней нормали к траектории
   
4. 
   В сторону вогнутости траектории
   
5. 
   В сторону выпуклости траектории
   

447.

Проекции скорости при координатном способе задания движения это

1. 
   Проекции радиус- вектора точки r на оси координат
   
2. 
   Вторые производные от координат точки
   
3. 
   Первые производные от координат точки
   
4. 
   Производные от радиус-вектора точки
   
5. 
   Производные от криволинейной координаты
   

448.

Величина скорости точки при координатном способе задания движения равна

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   

449.

Определить величину скорости точки при естественном способе задания движения.

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   

550.

Проекции вектора ускорения точки при координатном способе задания движения это

1. 
   Проекции радиус-вектора точки r на оси координат
   
2. 
   Вторые производные от координат точки
   
3. 
   Первые производные от координат точки
   
4. 
   Производные от радиус-вектора точки
   
5. 
   Производные от криволинейной координаты
   

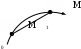551.

Точка движется в пространстве по криволинейной траектории из М₀ в М₁. Определить направление вектора средней скорости на указанном перемещении.

1. 
   По касательной к траектории в точке М₀
   
2. 
   По касательной к траектории в точке М₁
   
3. 
   К центру кривизны траектории в точке М₀
   
4. 
   По хорде М₀М₁
   
5. 
   К центру кривизны траектории в точке М₁
   

1

2

3

552.

Радиус-вектор точки , где a, b, c – константы, - орты неподвижных осей. Найти вектор скорости точки

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   

553.

Радиус-вектор точки , где a, b, c – константы, - орты неподвижных осей. Определить вектор ускорения точки

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   

554.

Движение точки задано в координатной форме уравнениями x = 3t, y = 9t²+6. Найти уравнение траектории

1. 
   y = 3x
   
2. 
   
   
3. 
   
   
4. 
   y = 3x² + 6
   
5. 
   
   

555.

Для условий задачи 54 найти модуль вектора скорости

1. 
   
   
2. 
   v = 3 + 18 t
   
3. 
   
   
4. 
   v = 3t + 9 t² + 6
   
5. 
   
   

556.

Для условий задачи 54 найти модуль ускорения точки

1. 
   
   
2. 
   
   
3. 
   w = 18t + 6
   
4. 
   
   
5. 
   w = 18
   

557.

Закон движения точки , где - радиус- вектор положения точки. Определить мгновенное ускорение

1. ; 2. ;

3. ; 4. ; 5. .

558.

Нормальное ускорение при естественном способе задания движения точки равно

1. ; 2. ;

3. ; 4. ;

5. .

559.

Какое из равенств дает величину касательного ускорения?

1. ; 2.