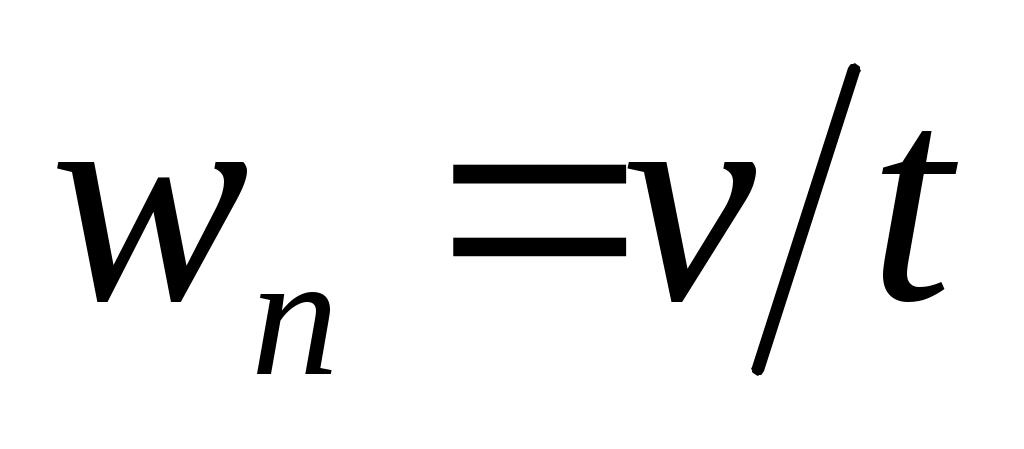 ;
;
3. 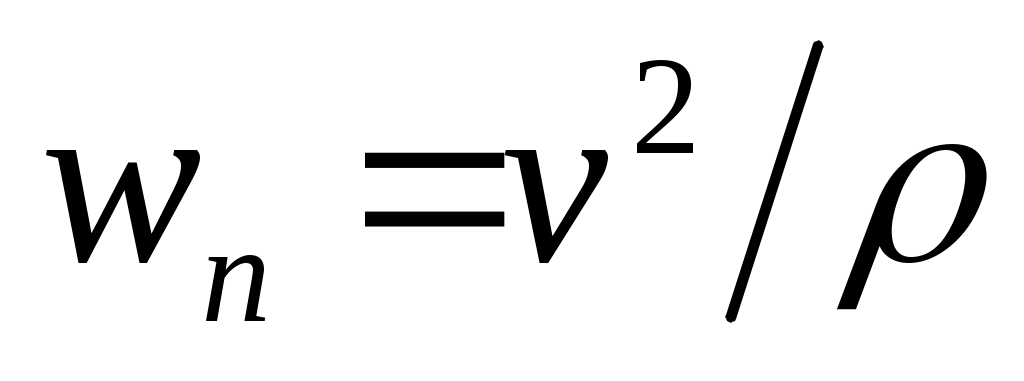 ; 4.
; 4. 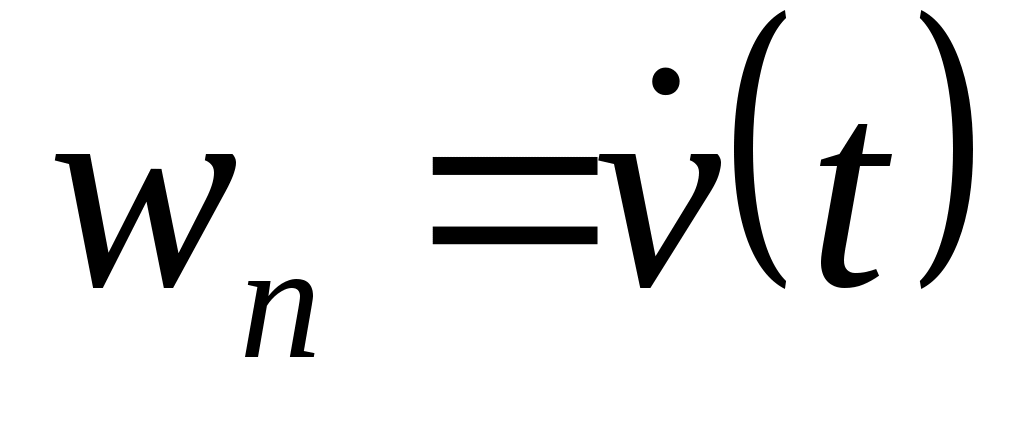 ;
;
5. 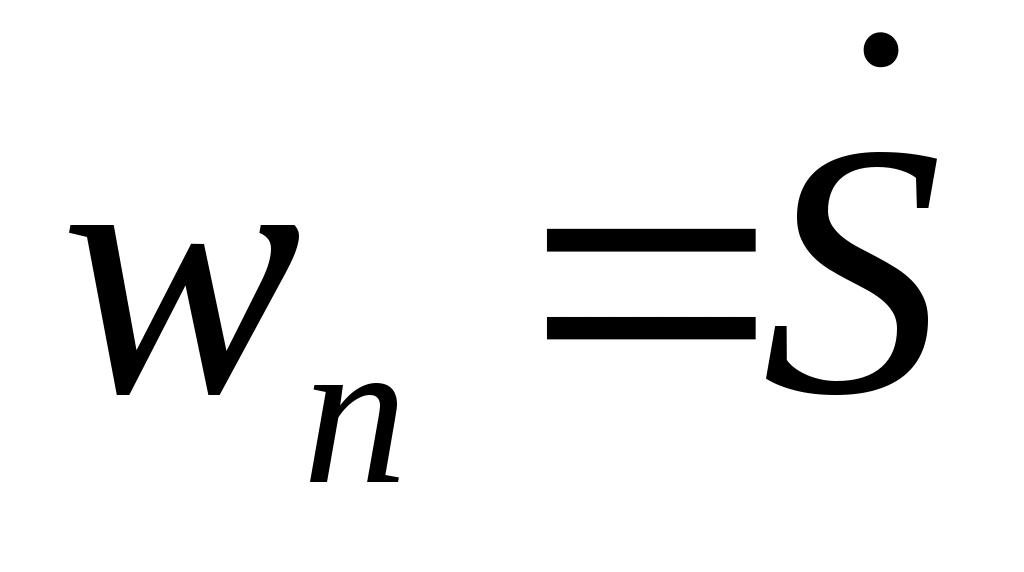 .
.
1
|
2
|
3
|
660.
|
Точка движется по окружности радиуса R с постоянной по модулю скоростью v. Укажите направление вектора ускорения?
|
 направлен по радиусу окружности к её центру направлен по радиусу окружности к её центру
 направлен в сторону вектора скорости направлен в сторону вектора скорости
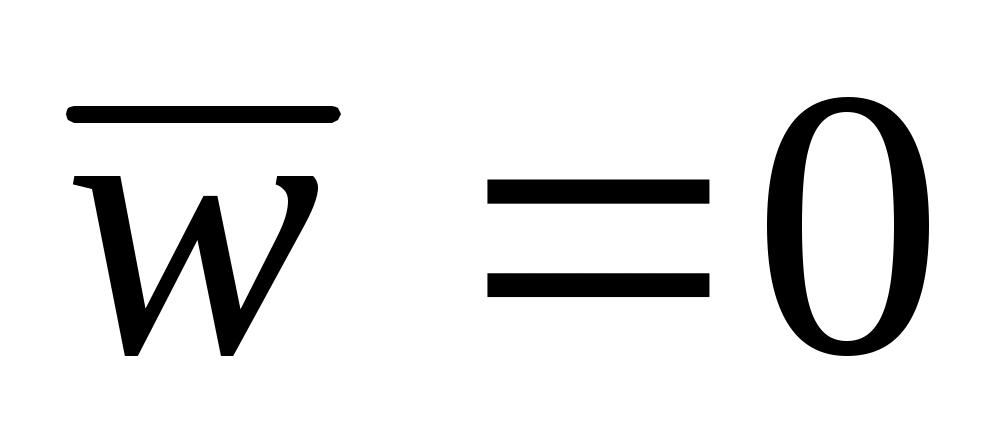
 направлен по секущей направлен по секущей
 направлен в сторону внешней нормали направлен в сторону внешней нормали
|
661.
|
Чему равно нормальное ускорение в условиях предыдущей задачи?
|
1. 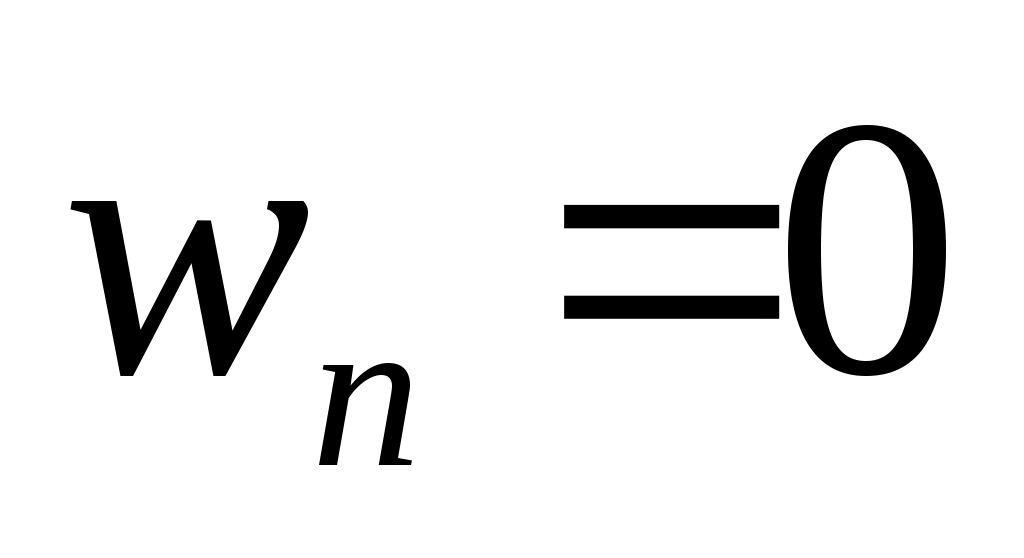 ; 2. ; 2. 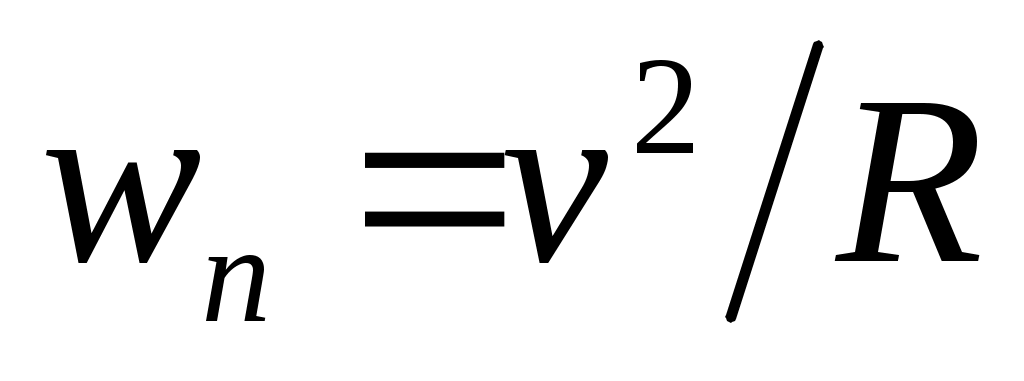 ; 3. ; 3. 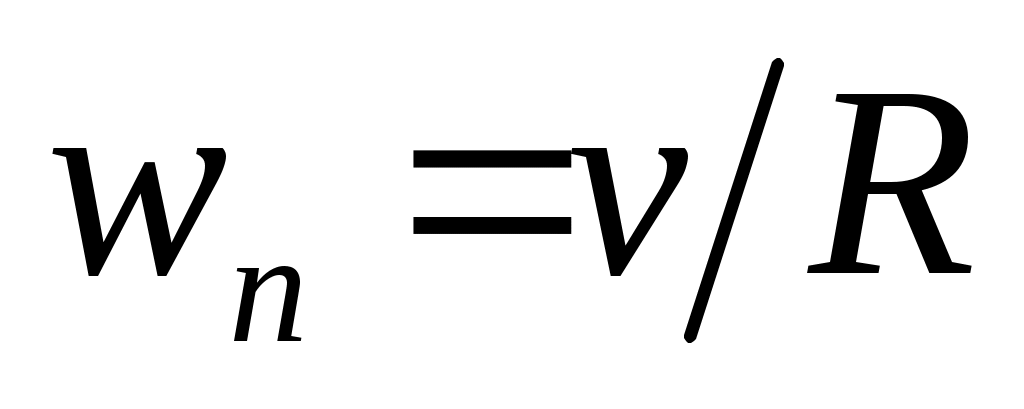 ; ;
4. 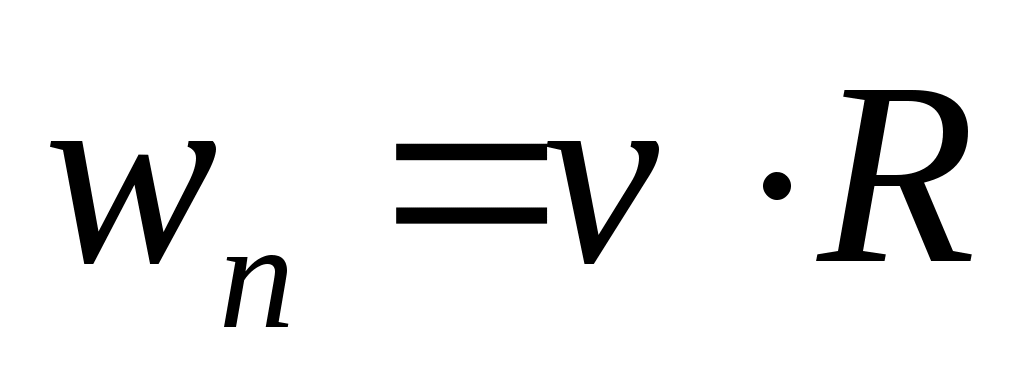 ; 5. ; 5. 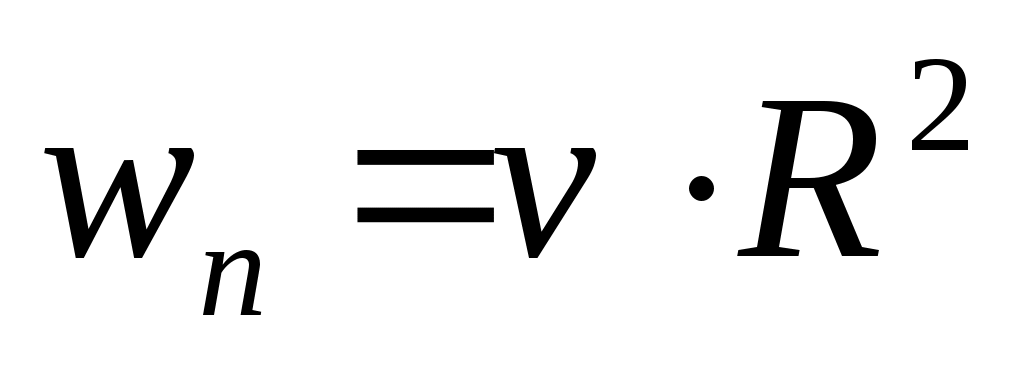 . .
|
662.
|
Точка движется по окружности радиуса R. Найти радиус кривизны траектории
|
1.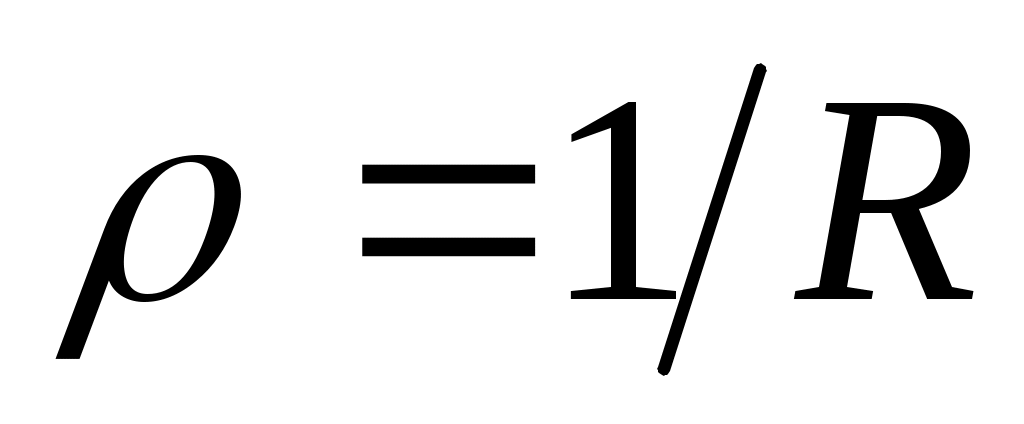 ; 2. = ; 3. = 1; ; 2. = ; 3. = 1;
4. = R2; 5. = R
|
663.
|
Угол между векторами скорости и ускорения – острый. Как движется точка?
|
Прямолинейно
Замедленно
Ускоренно
Равноускоренно
Равномерно
|
664.
|
Точка падает вертикально с постоянным ускорением g. Какому равенству при этом удовлетворяет величина ее скорости и пройденный путь?
|
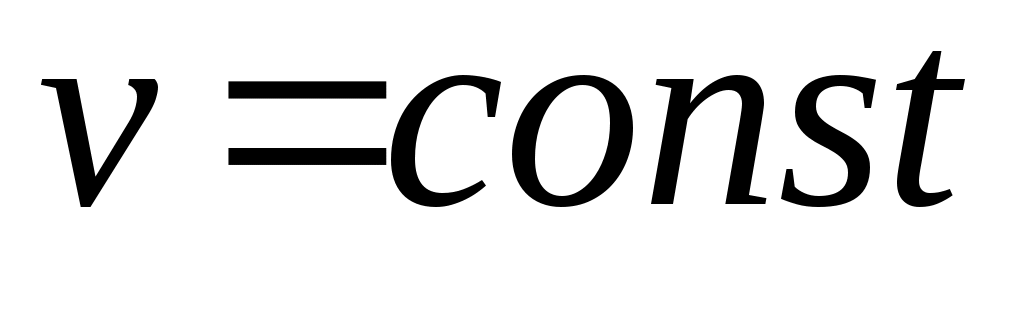
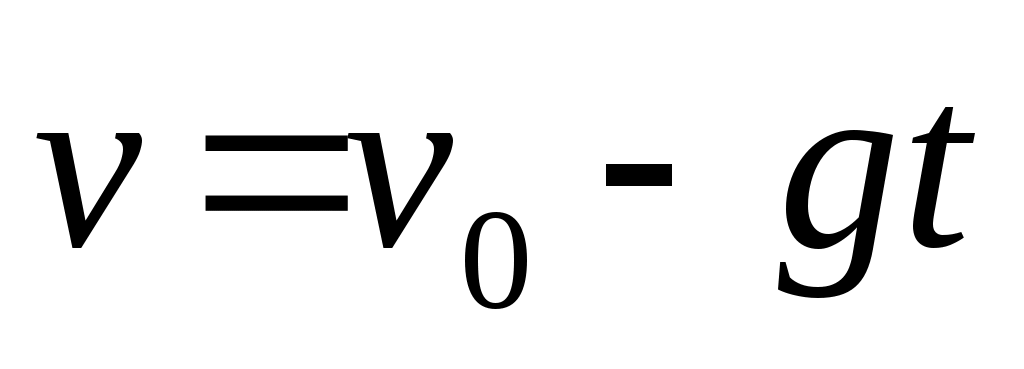
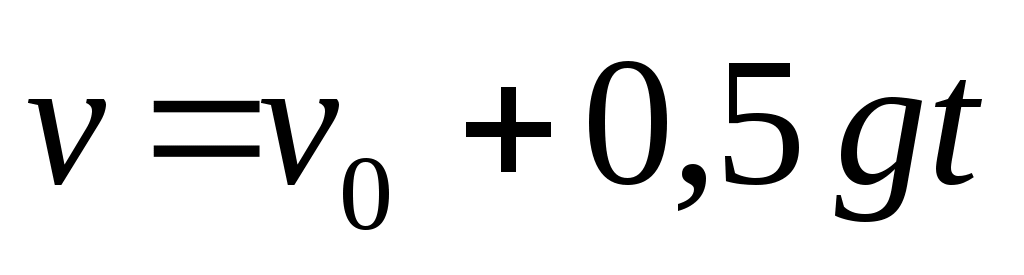
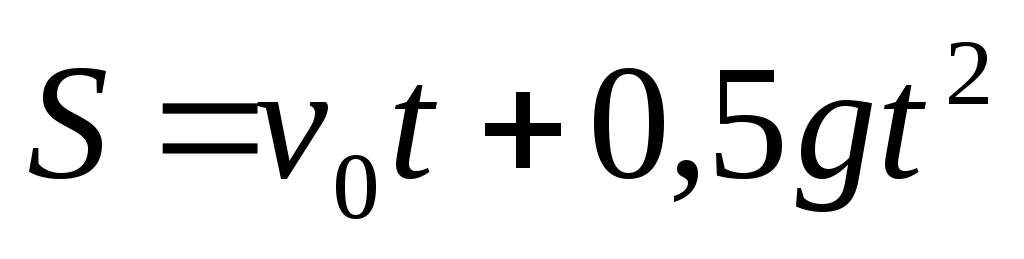
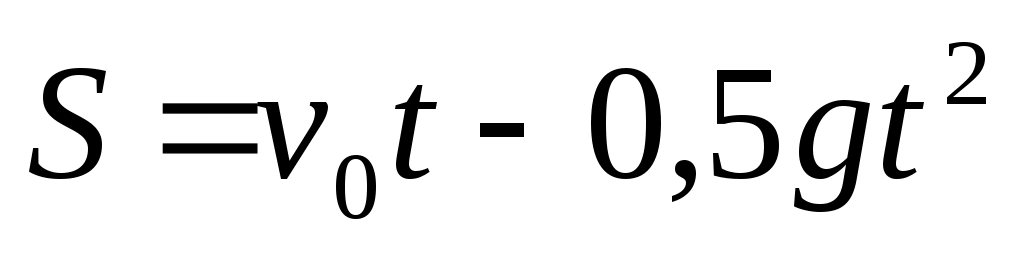
|
665.
|
При поступательном движении твердого тела точка А имеет скорость 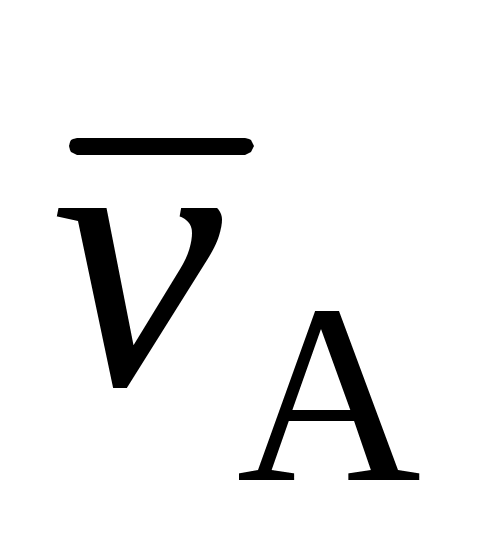 . Чему равна скорость точки В этого тела, отстоящей от А на расстояние h? . Чему равна скорость точки В этого тела, отстоящей от А на расстояние h?
|
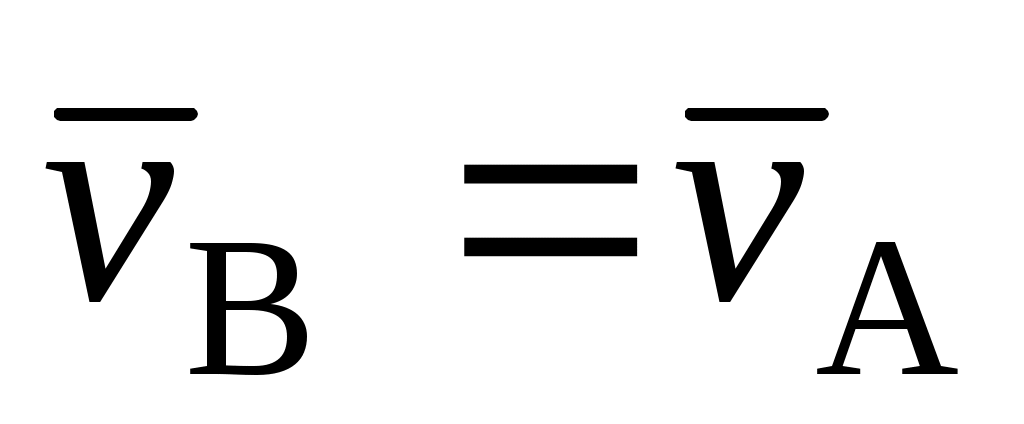
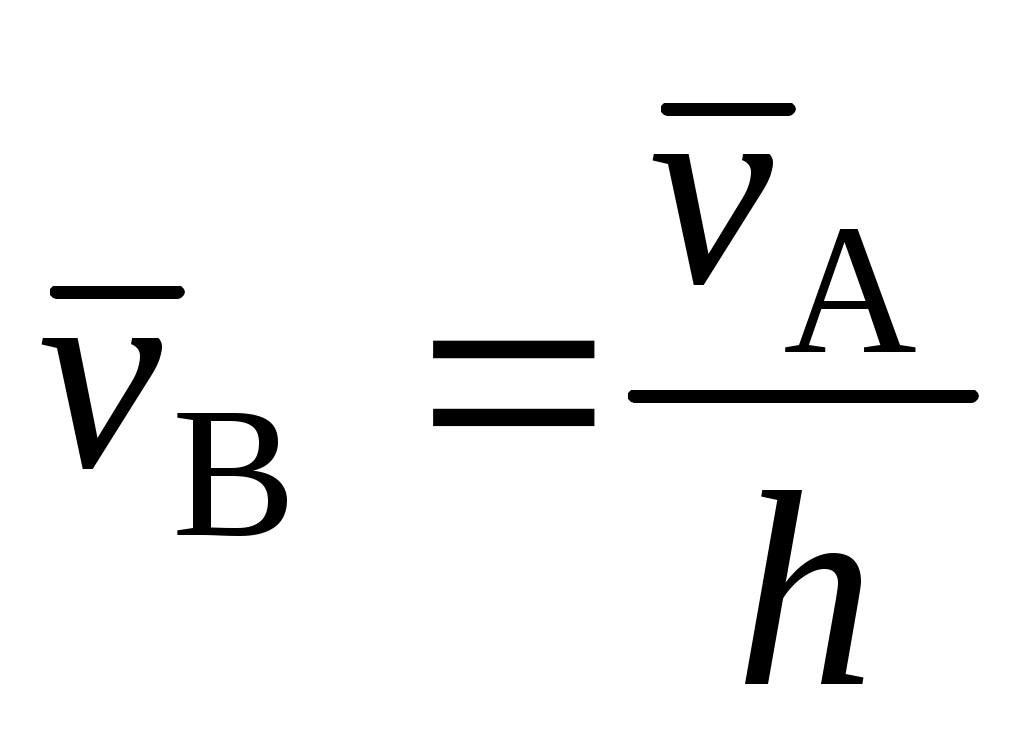
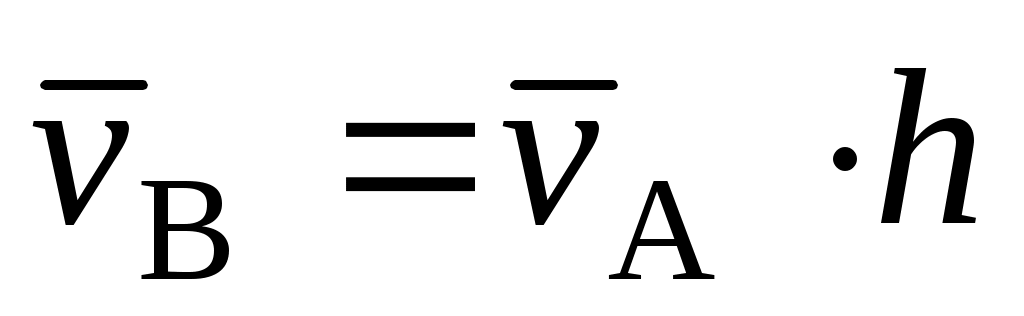
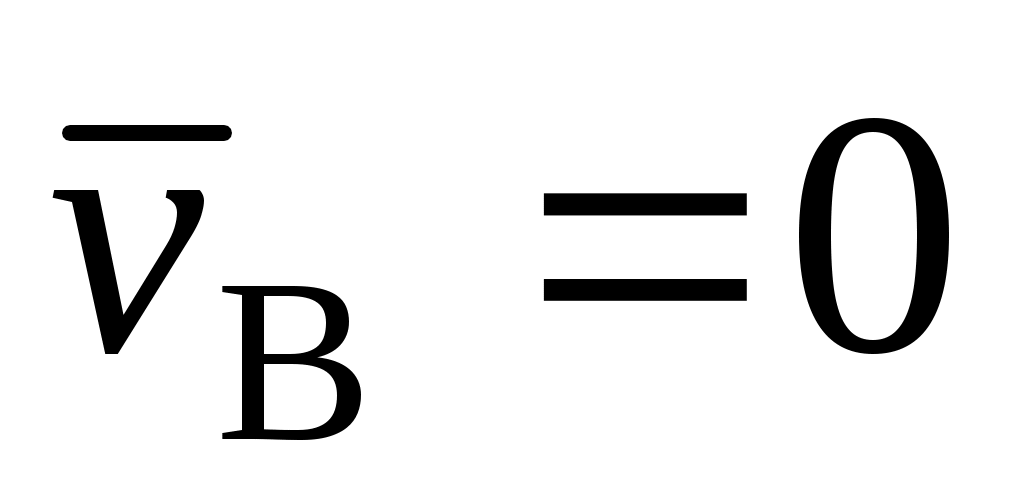
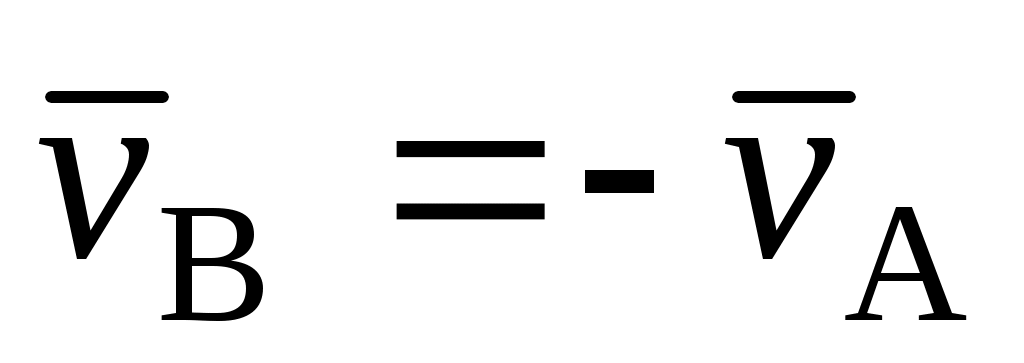
|
666.
|
Угловая скорость вращения тела вокруг неподвижной оси  . Определить нормальное ускорение точки, находящейся на расстоянии h от оси вращения. . Определить нормальное ускорение точки, находящейся на расстоянии h от оси вращения.
|
1. 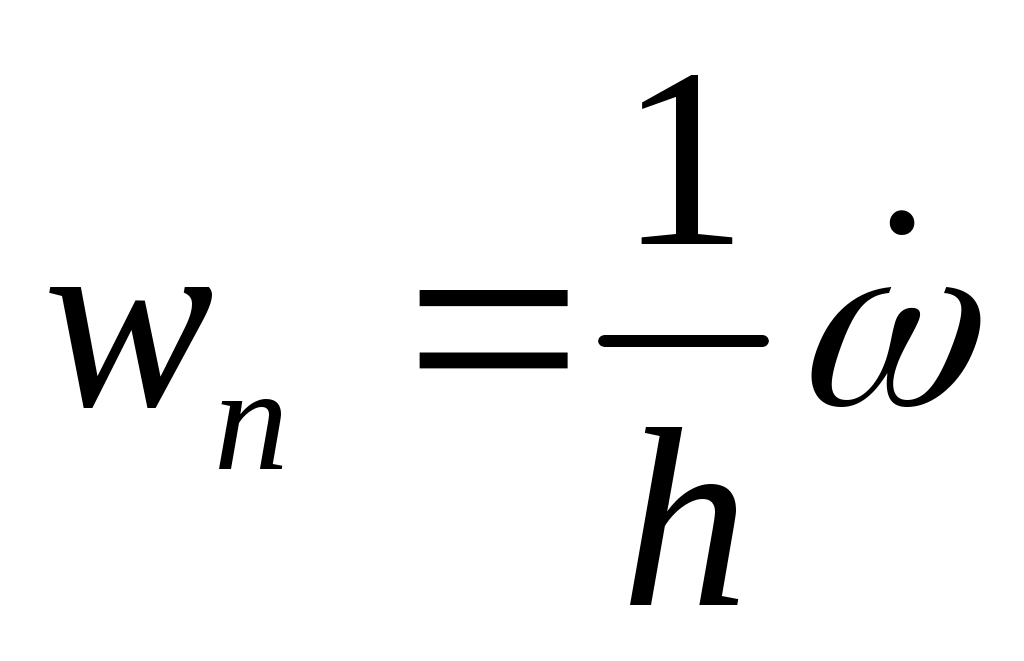 ; 2. ; 2. 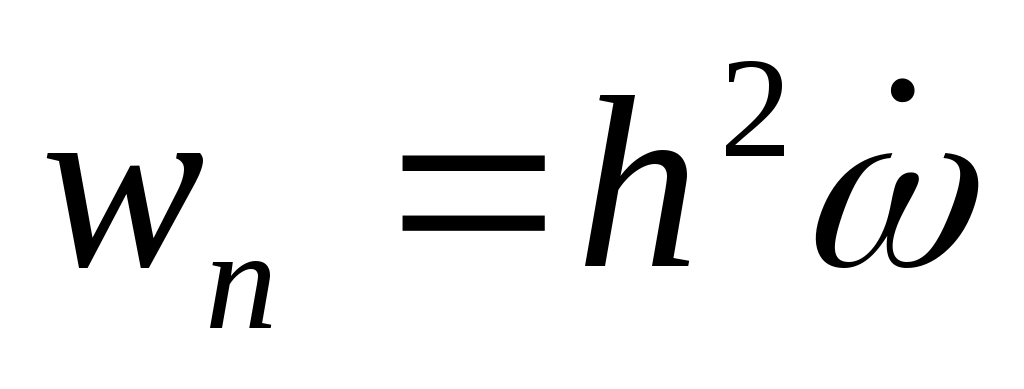 ; ;
3. 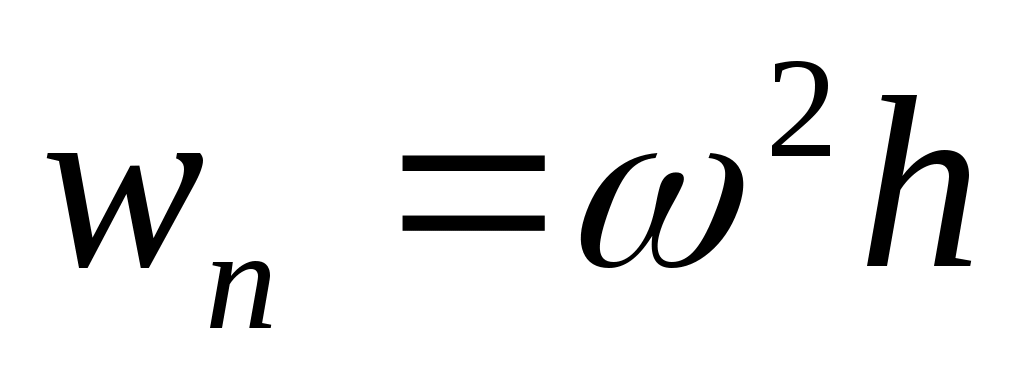 ; 4. ; 4. 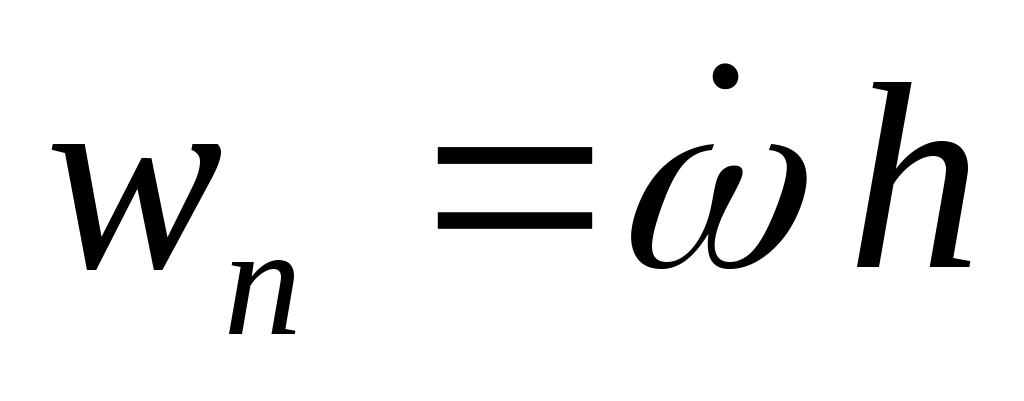 ; ;
5. 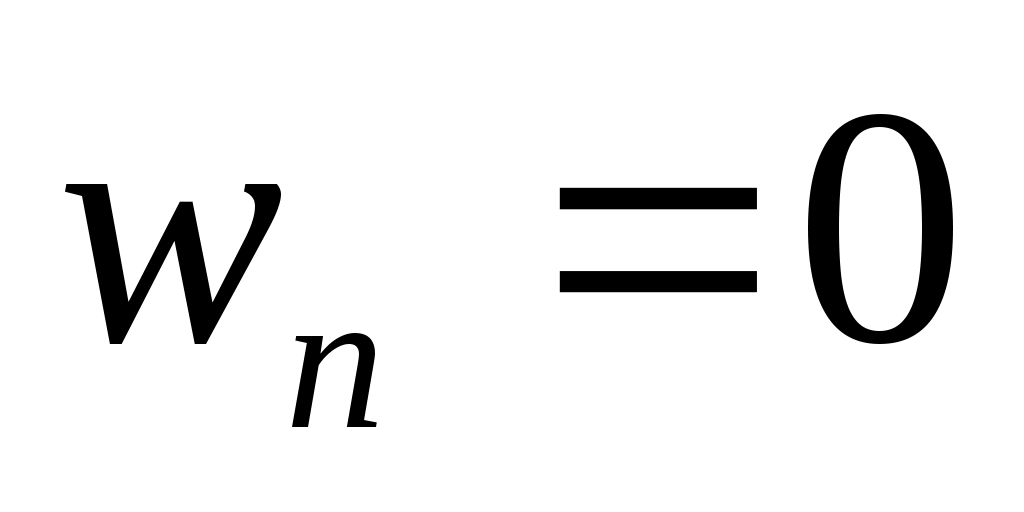
|
667.
|
Какое из равенств дает величину касательного ускорения во вращательном движении?
|
1. 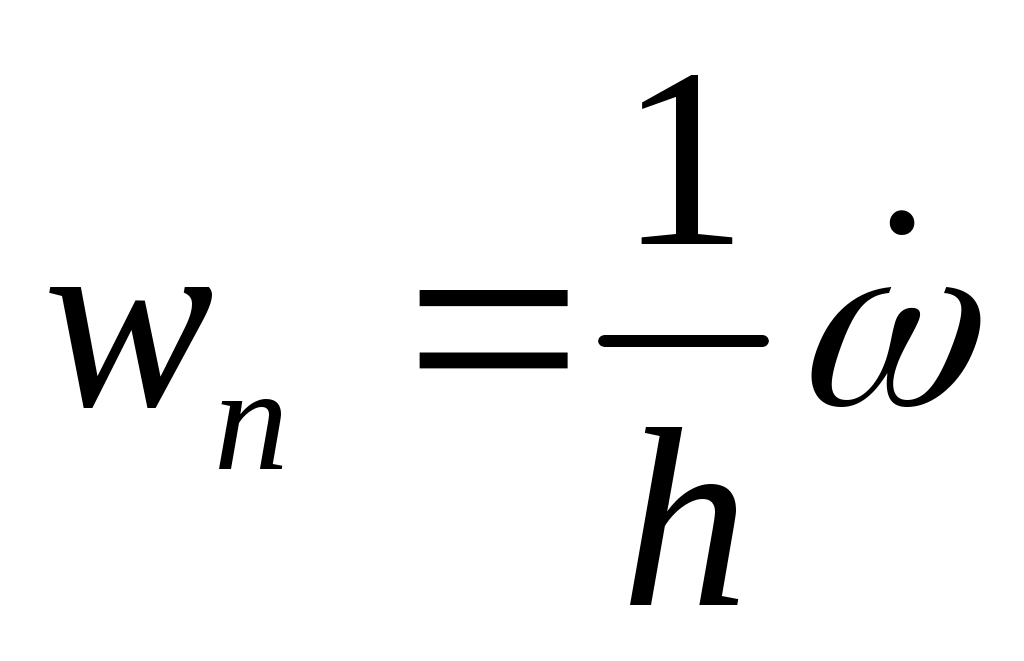 ; 2. ; 2. 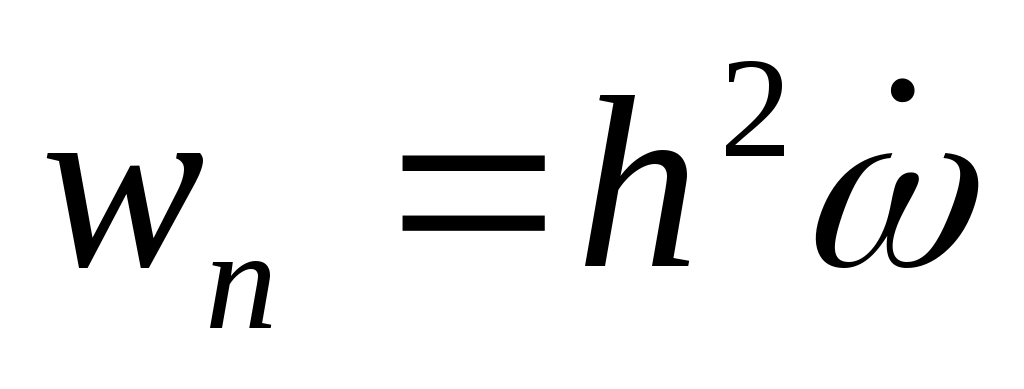 ; ;
3. 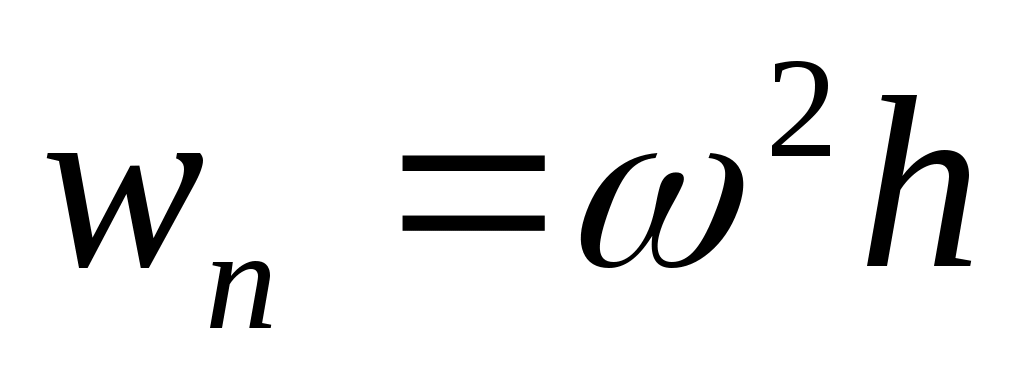 ; 4. ; 4. 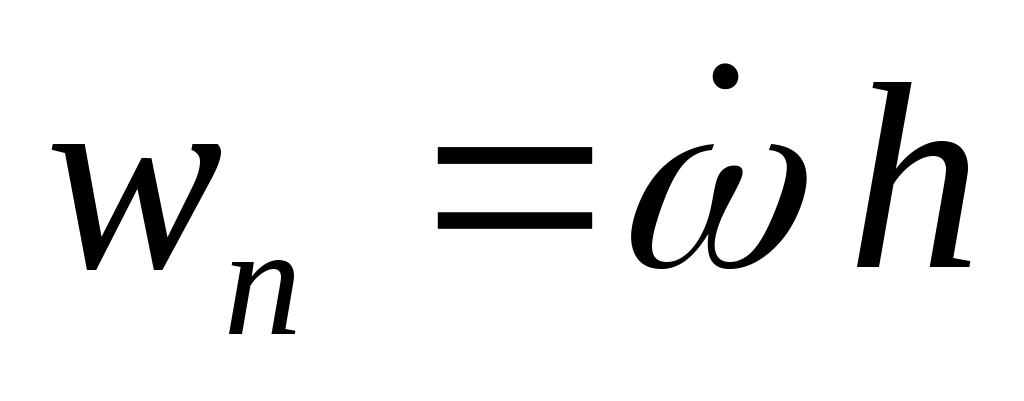 ; 5. ; 5. 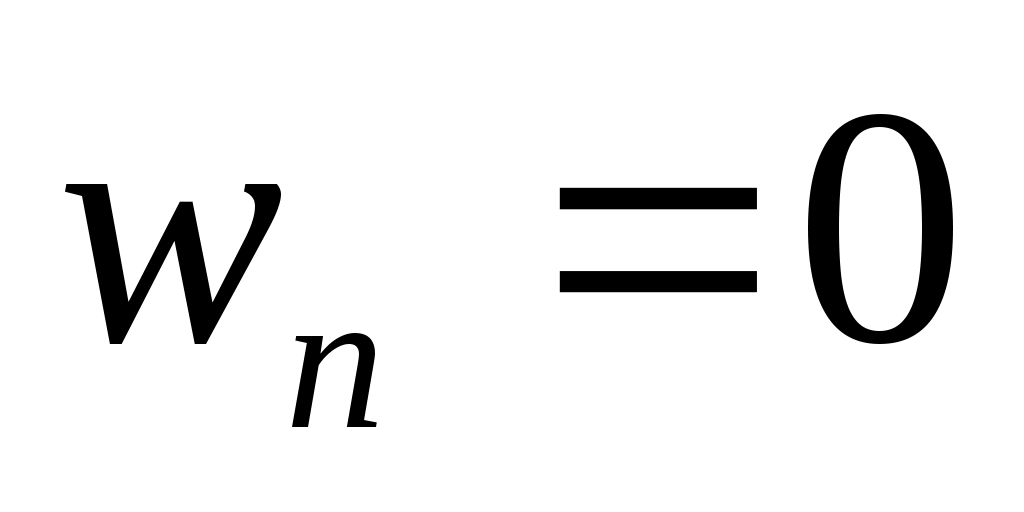
|
668.
|
Тело вращается равноускоренно из состояния покоя. Как изменяется его угол поворота?
|
1. 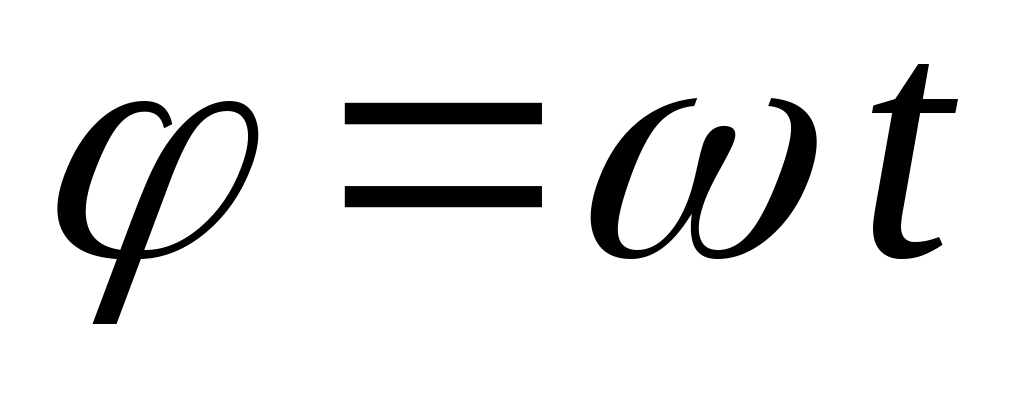 ; 2. ; 2. 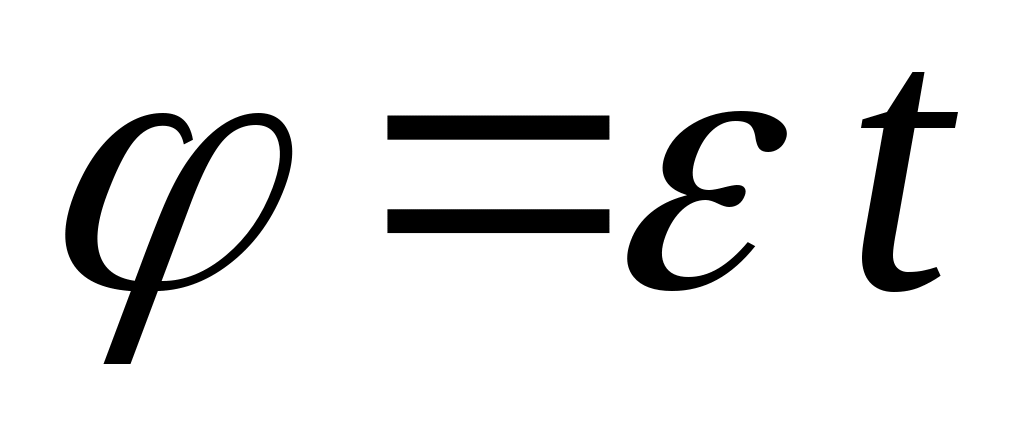 ; ;
3. 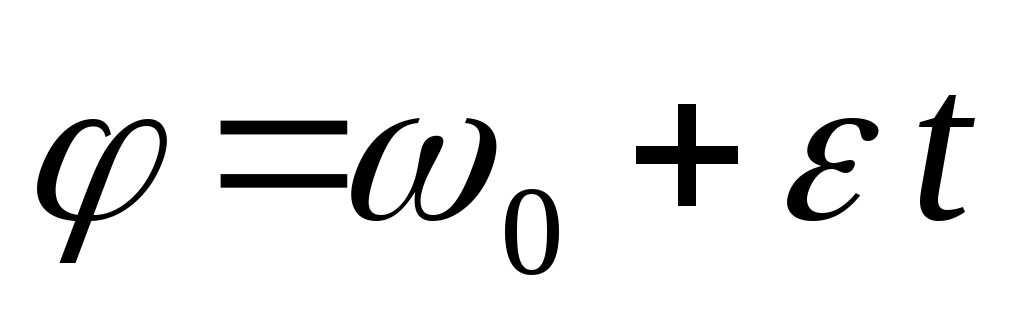 ; 4. ; 4. 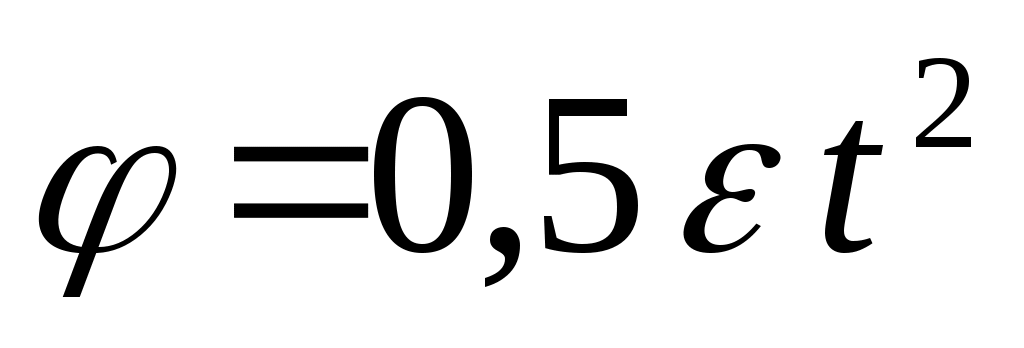 ; ;
5. 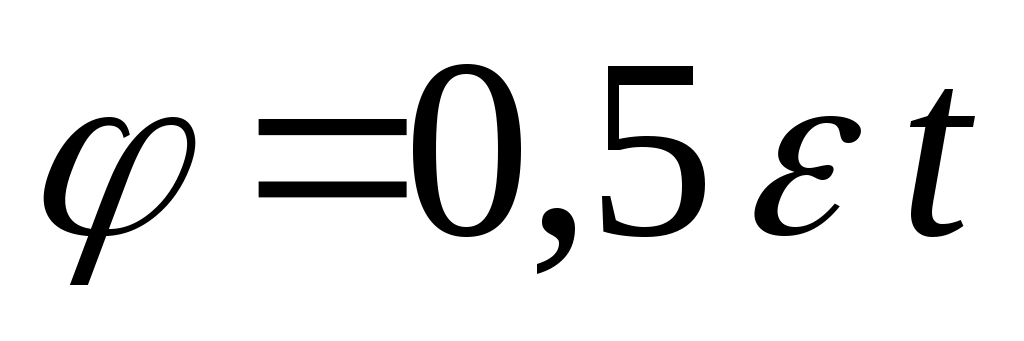 ; ;
|
669.
|
Тело вращается равноускоренно из состояния покоя. Определить закон изменения угловой скорости.
|
1. 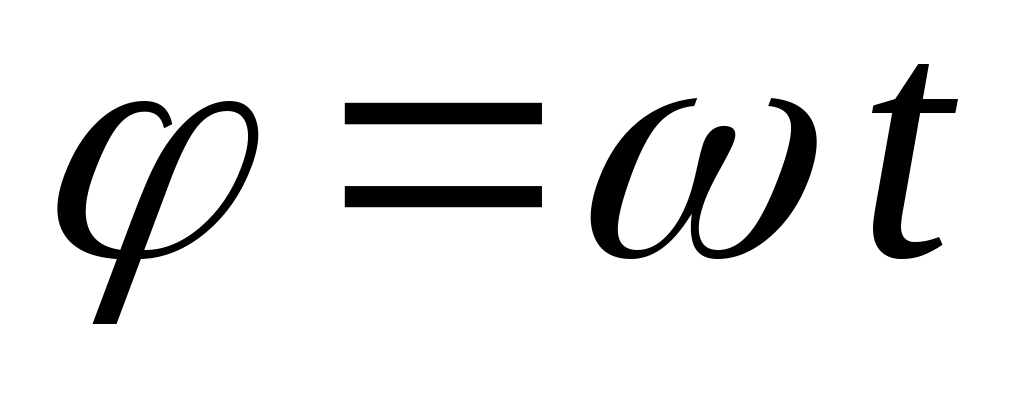 ; 2. ; 2. 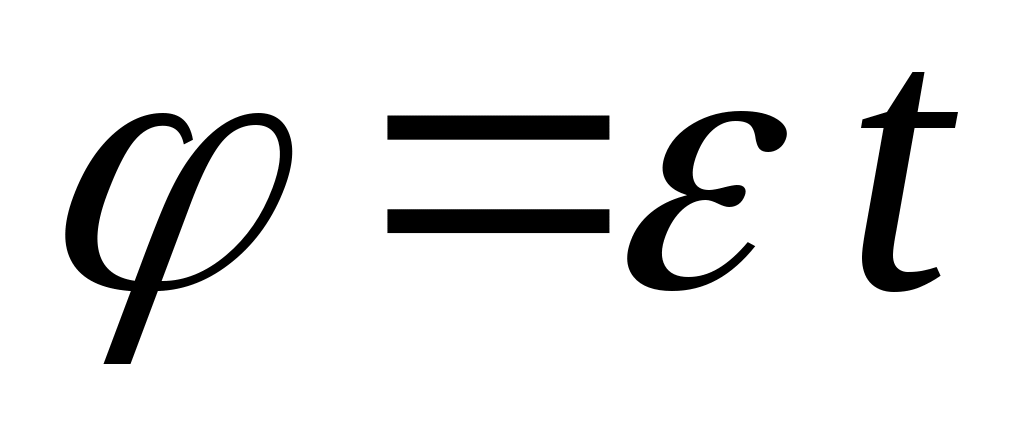 ; ;
3. 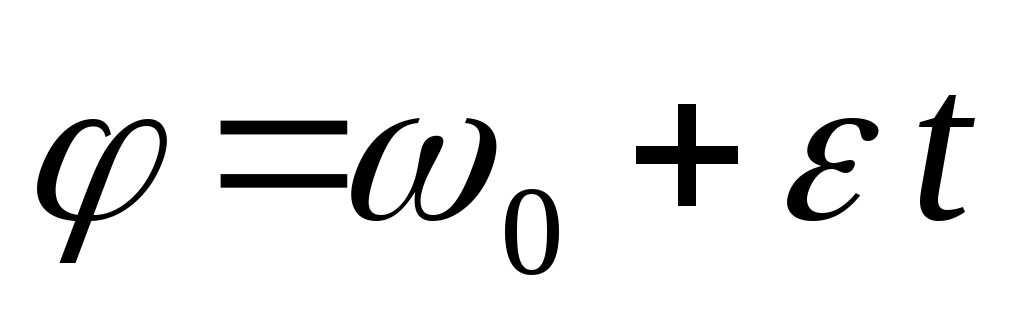 ; 4. ; 4. 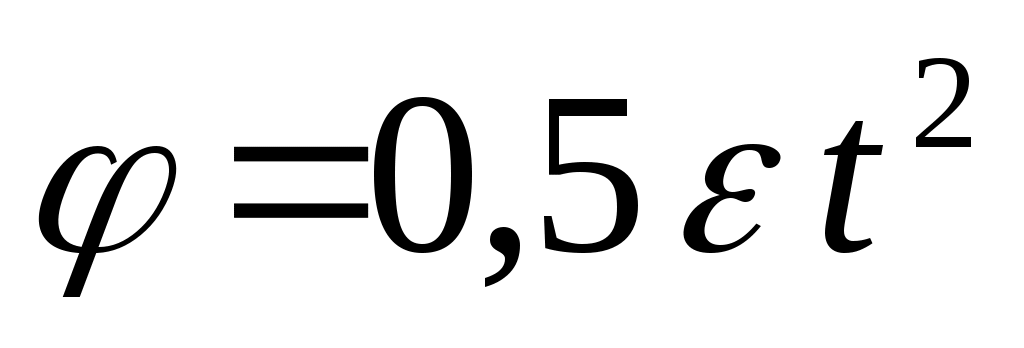 ; ;
5. 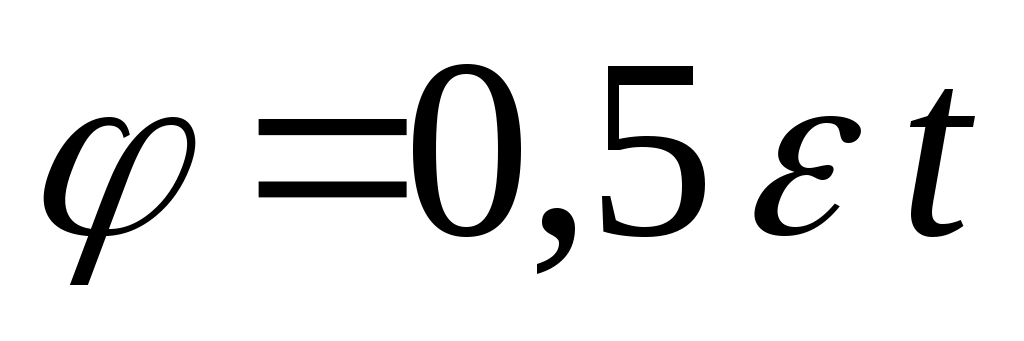 ; ;
|
1
|
2
|
3
|
770.
|
Как называется движение точки относительно подвижной системы координат, которая в свою очередь движется относительно неподвижной системы координат?
|
Абсолютным
Относительным
Переносным
Поступательным
Вращательным
|
771.
|
Теорема сложения скоростей при сложном движении точки записывается так
|
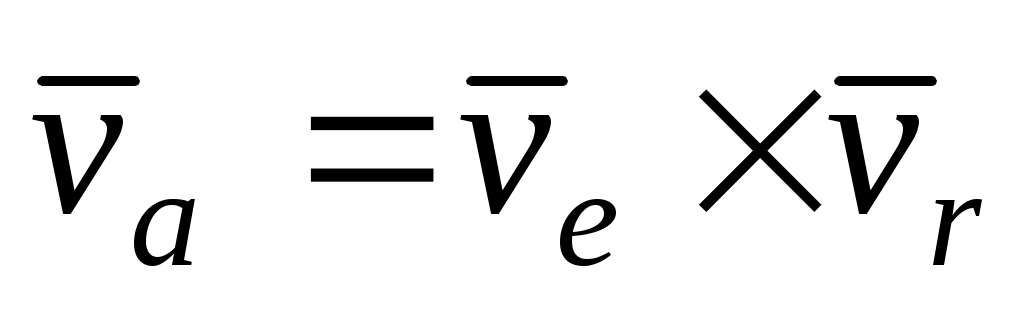
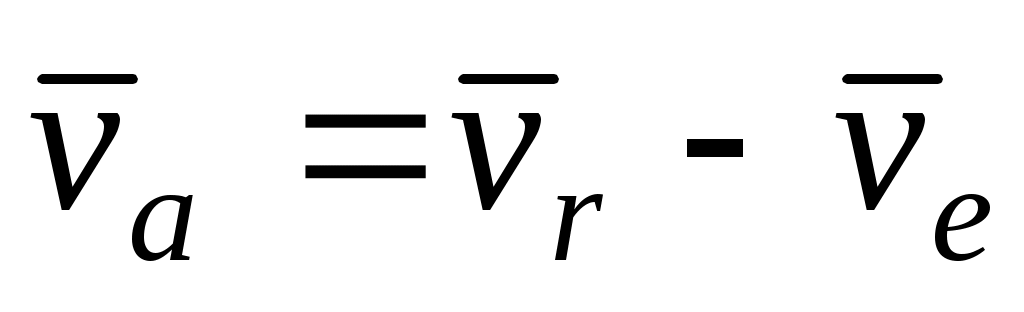
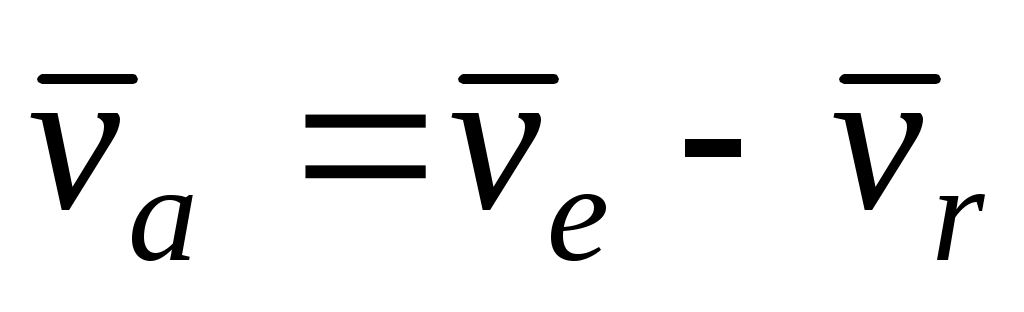
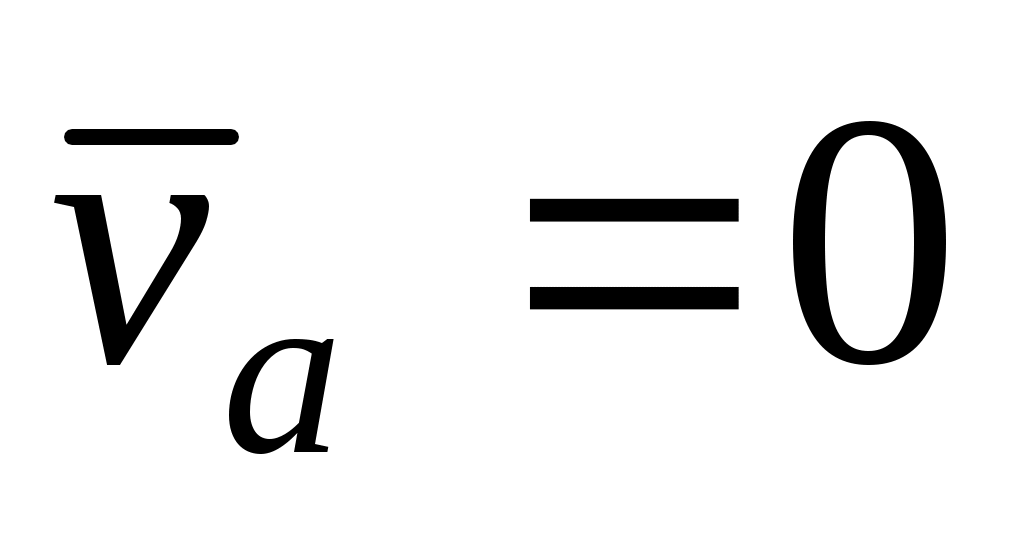
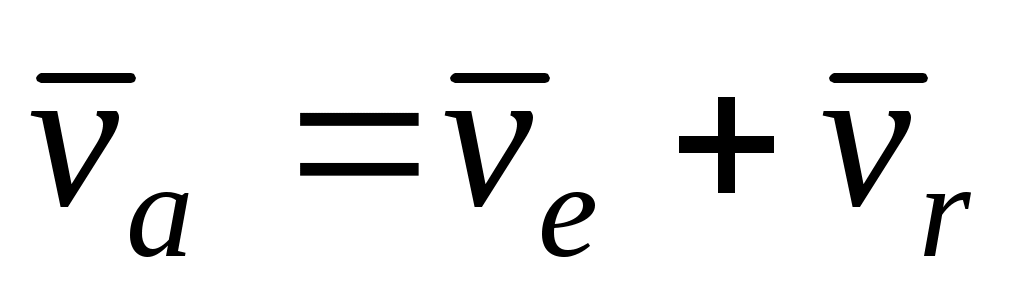
|
772.
|
Переносная среда вращается с угловой скоростью 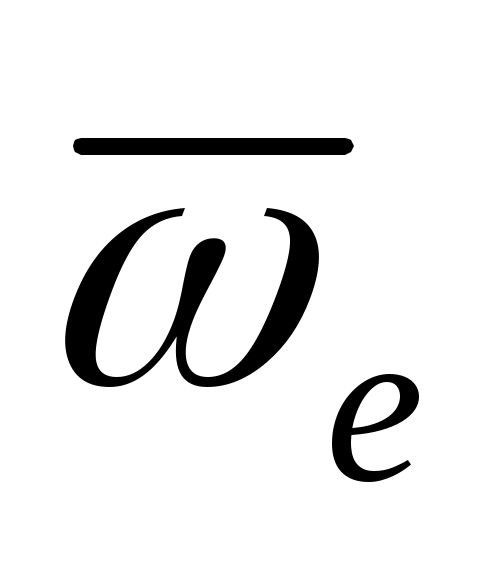 , относительно нее движется точка со скоростью , относительно нее движется точка со скоростью 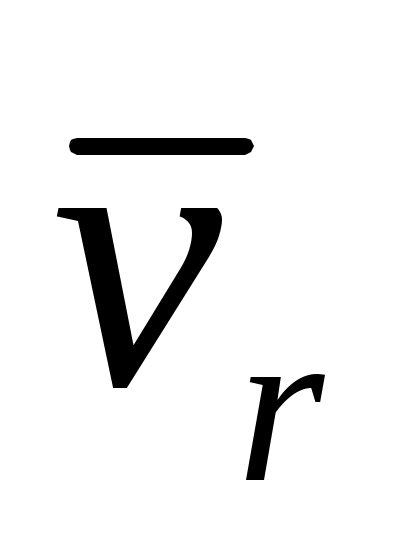 . Чему равно ускорение Кориолиса? . Чему равно ускорение Кориолиса?
|
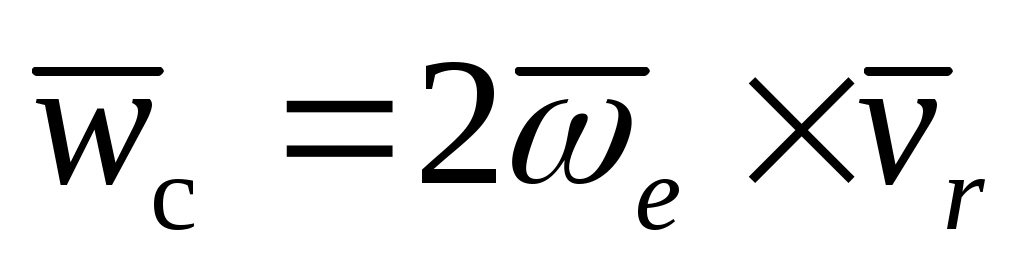
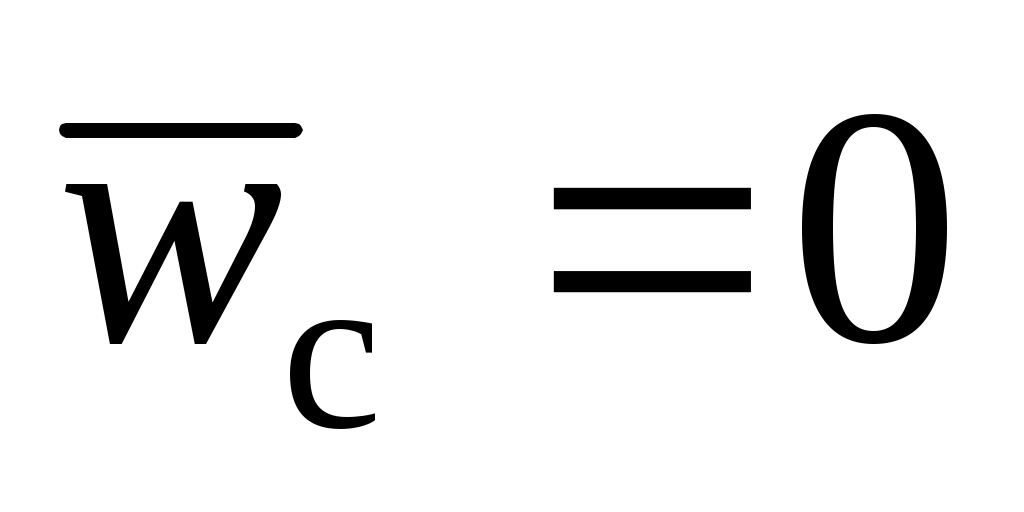
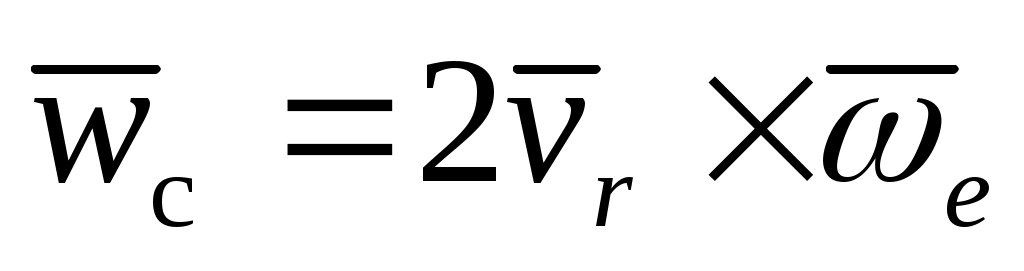
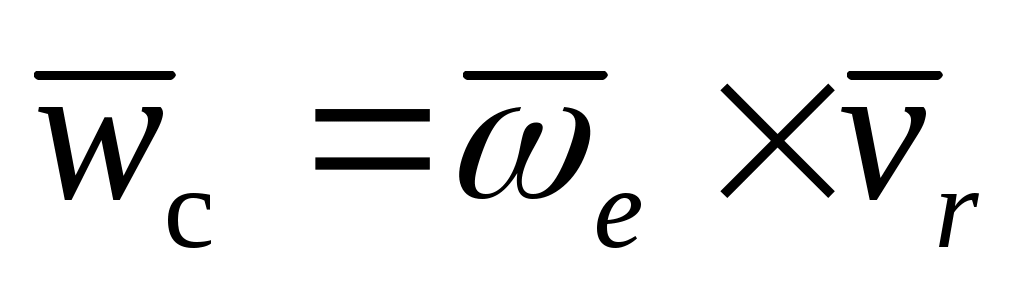
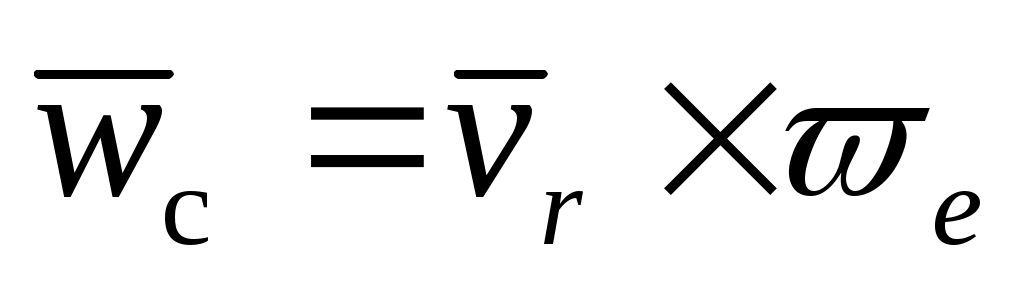
|
773.
|
Диск движется поступательно со скоростью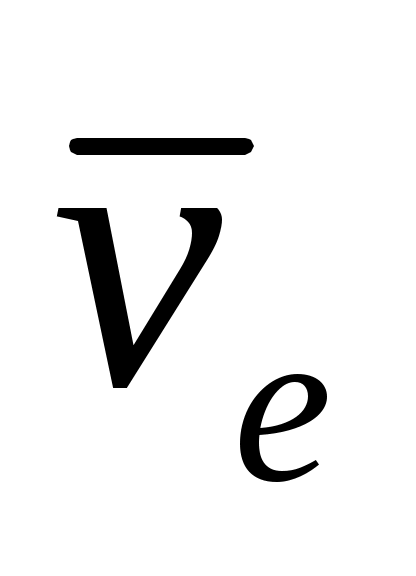 , по его ободу вращается точка со скоростью , по его ободу вращается точка со скоростью 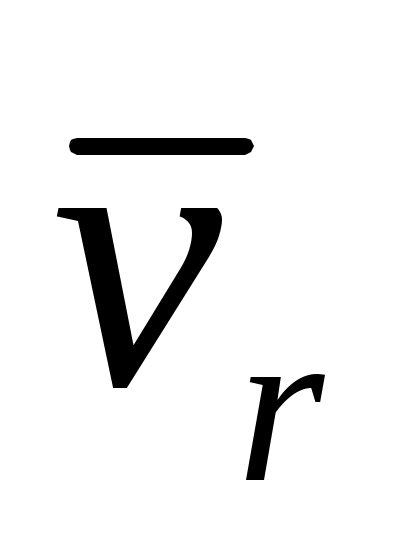 . Определить для нее ускорение Кориолиса. . Определить для нее ускорение Кориолиса.
|
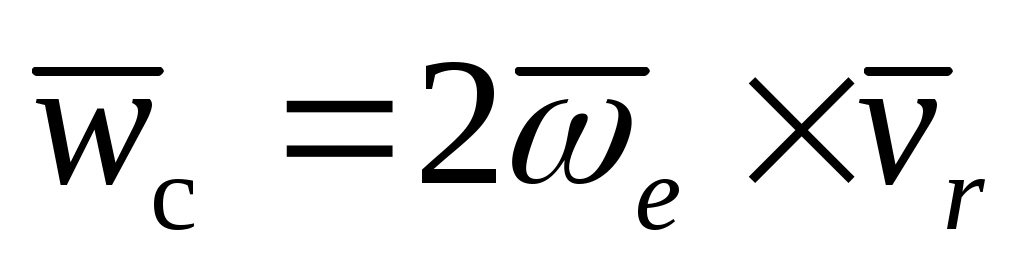
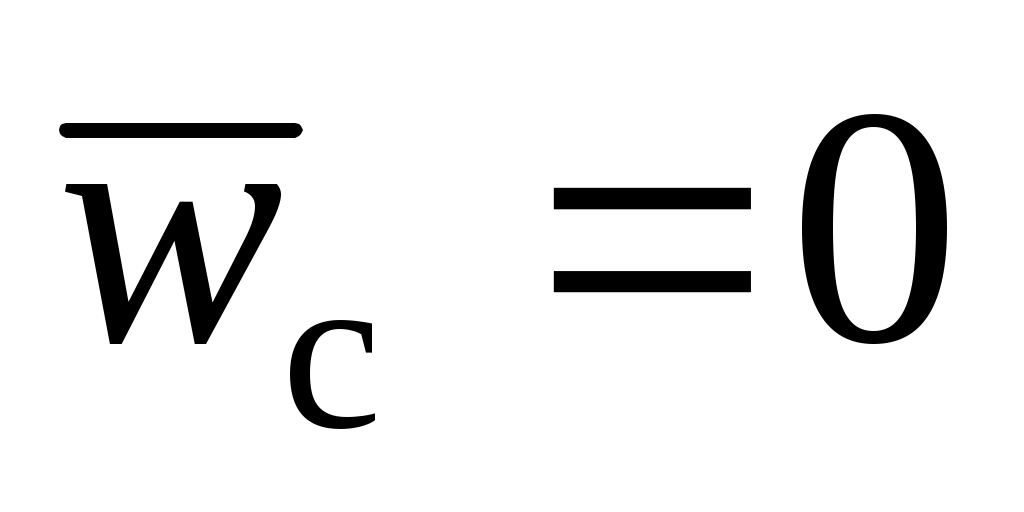
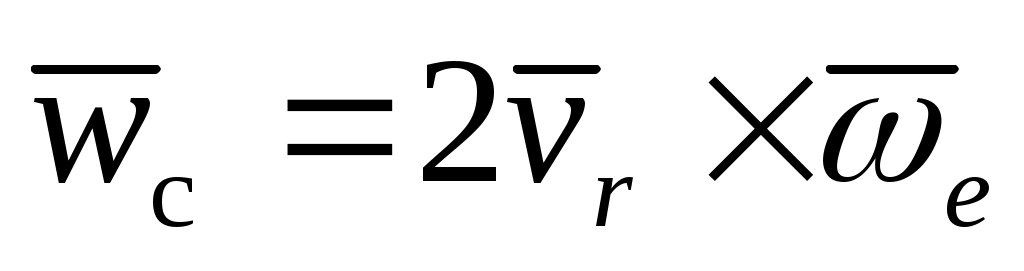
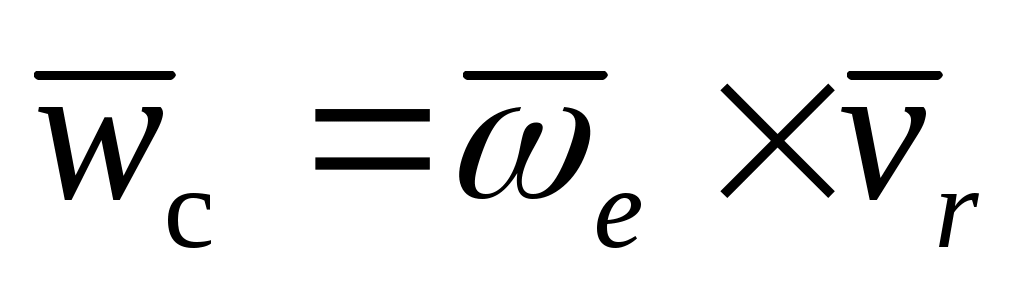
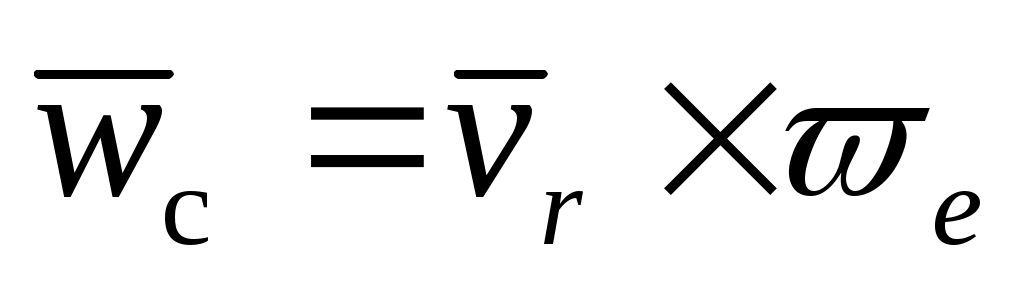
|
774.
|
Найти величину скорости точки А плоской фигуры, если P и  – мгновенный центр скоростей и ее угловая скорость при плоском движении. – мгновенный центр скоростей и ее угловая скорость при плоском движении.
|
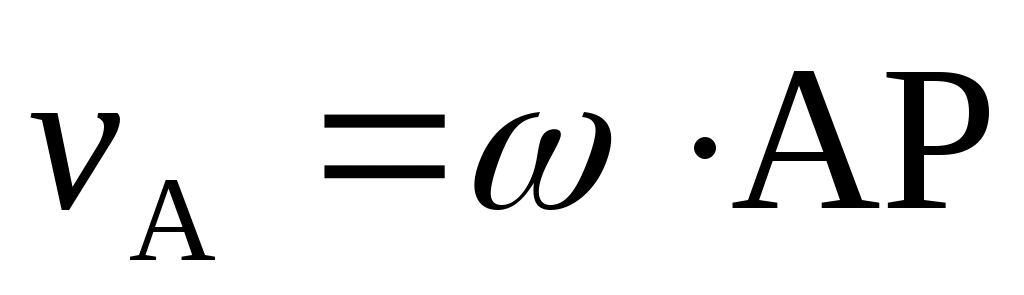
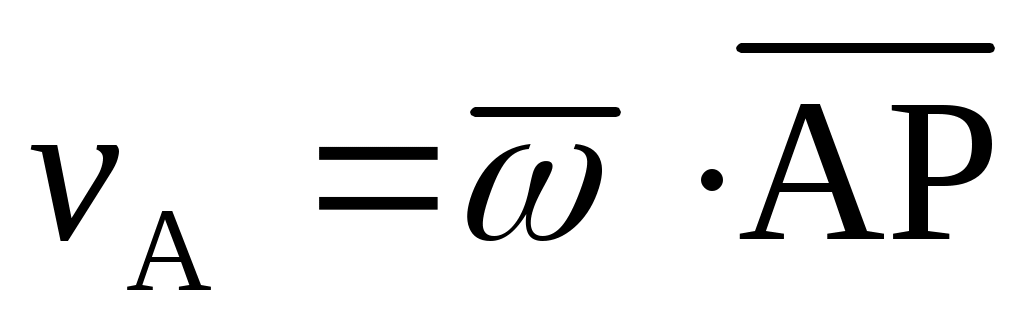
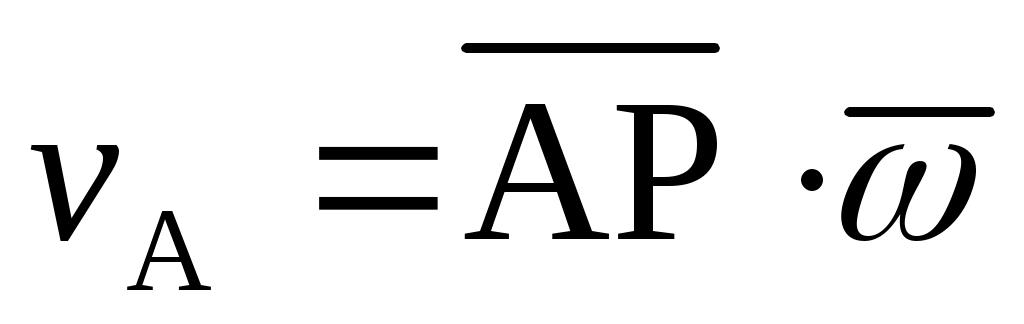
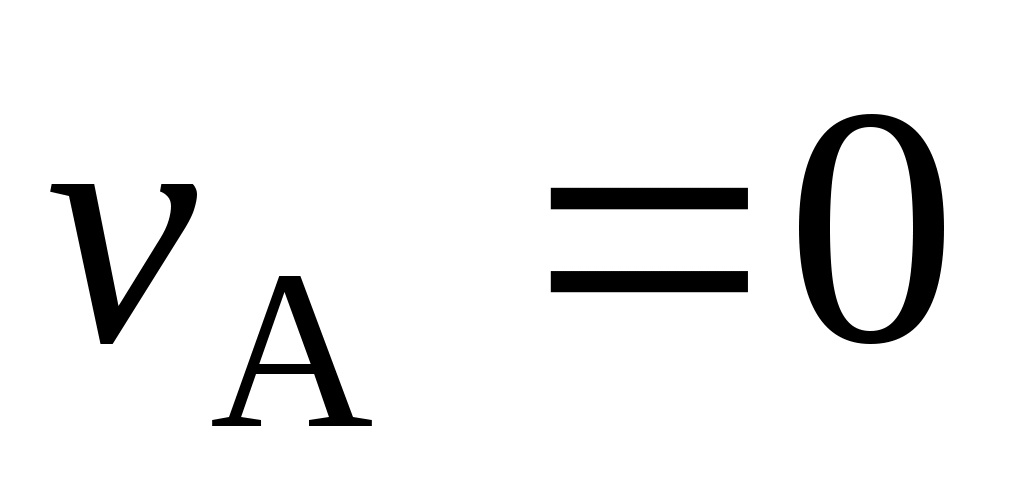
vA = vP
|
775.
|
Скорости двух точек плоской фигуры равны по величине и не параллельны. Где находится мгновенный центр скоростей?
|
На бесконечности.
В одной из этих двух точек.
Рядом с плоской фигурой.
На пересечении радиусов кривизны траекторий точек.
На пересечении перпендикуляров к скоростям точек.
|
 Скачать 0.58 Mb.
Скачать 0.58 Mb.