тесты по геометрии. Тесты по двум разделам Радел 1 включает тему Векторы в пространстве. Метод координат в пространстве
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Раздел №2 тест по теме: «Прямоугольный параллелепипед» Вариант №1 Уровень А 1. Развёрткой прямоугольного параллелепипеда является фигура под номером… 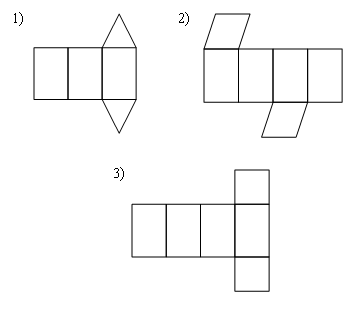 2. ABCD – квадрат, Тогда верно, что… 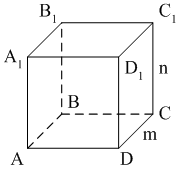 1) 2) 3) 3. Все шесть граней прямоугольники … 1) у наклонного параллелепипеда; 2) прямого параллелепипеда; 3) прямоугольного параллелепипеда. 4. В прямоугольном параллелепипеде неверно, что… 1) диагонали параллелепипеда равны; 2) диагонали всех боковых граней равны; 3) диагонали оснований равны. 5. ABCDA1B1C1D1 – куб. DB1 = d. Тогда площадь полной поверхности куба равна… 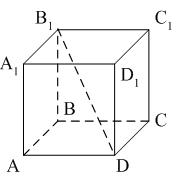 1) 2d2; 2) 3d2; 3) 6d2. 6. ABCDA1B1C1D1 – прямоугольный параллелепипед. Тогда неверно, что… 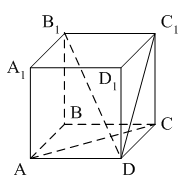 1) 2) 3) 7. Какое утверждение неверное? 1) Куб – это прямоугольный параллелепипед с равными рёбрами. 2) Если в параллелепипеде все рёбра равны, то он является кубом. 3) Не могут боковые грани куба быть не квадратами. 8. Угол между диагональю B1D прямоугольного параллелепипеда ABCDA1B1C1D1 и плоскостью (DCC1) – это угол… 1) B1DC; 2) B1DC1; 3) B1DB. Уровень B 1. Измерения прямоугольного параллелепипед равны 6 см, 8 см и 3 см. Тогда площадь полной поверхности параллелепипеда равна… 2. Измерения прямоугольного параллелепипеда равны 3. ABCDA1B1C1D1 – прямоугольный параллелепипед. АВ = 7 см, ВС = 24 см, АА1 = 25 см. Тогда угол наклона диагонали параллелепипеда к плоскости основания равен… Вариант №2 Уровень А 1. Не является развёрткой прямоугольного параллелепипеда фигура под номером… 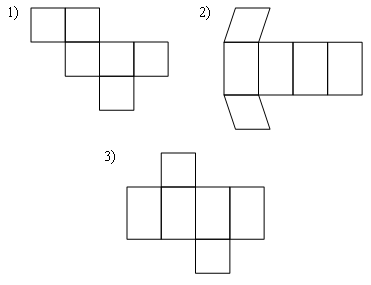 2. ABCDA1B1C1D1 – куб. АВ = m, DB1 = n. Тогда верно, что… 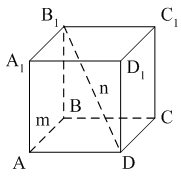 1)  2) 3) 3. Четыре грани – прямоугольники, а две – параллелограммы… 1) у наклонного параллелепипеда; 2) прямого параллелепипеда; 3) прямоугольного параллелепипеда. 4. Только в прямоугольном параллелепипеде верно, что… 1) противоположные грани равны и параллельны; 2) диагонали пересекаются в одной точке и делятся в ней пополам; 3) диагонали равны. 5. Какое предложение верное? 1) Всякие два диагональных сечения прямоугольного параллелепипеда пересекаются по его диагоналям. 2) В прямоугольном параллелепипеде все диагональные сечения равны. 3) В прямоугольном параллелепипеде все диагональные сечения – прямоугольники. 6. ABCDA1B1C1D1 – прямоугольный параллелепипед. Тогда неверно, что… 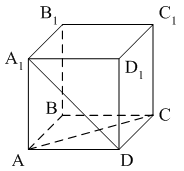 1) 2) 3) 7. Какое утверждение верное? 1) Не могут боковые грани прямоугольного параллелепипеда быть не прямоугольниками. 2) Прямоугольный параллелепипед – это куб. 3) Боковыми гранями куба не могут быть прямоугольники с равными смежными сторонами. 8. Угол между диагональю B1D прямоугольного параллелепипеда ABCDA1B1C1D1 и плоскостью (АВВ1) – это угол… 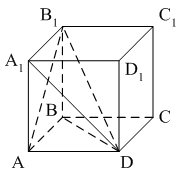 1) B1DB; 2) B1DA1; 3) AB1D. Уровень B 1. Измерения прямоугольного параллелепипеда равны 6 см, 4 см и 12 см. Тогда диагональ параллелепипеда равна… 2. Длина диагонали куба равна Тогда длина ребра куба равна… 3. ABCDA1B1C1D1 – прямоугольный параллелепипед. АВ = 3 см, ВС = 4 см. Угол наклона диагонали параллелепипеда к плоскости основания равен 45°. Тогда длина бокового ребра равна… тест по теме: «Тетраэдр и параллелепипед» Вариант №1 Уровень А 1. ABCD – тетраэдр. Тогда не являются противоположными рёбра… 1) AD и BC; 2) AC и DC; 3) AB и DC. 2. 12 – это число… 1) вершин параллелепипеда; 2) рёбер параллелепипеда; 3) граней параллелепипеда. 3. Какое предложение неверное? 1) Противоположные рёбра параллелепипеда параллельны и равны. 2) Противоположные грани параллелепипеда параллельны и равны. 3) Диагонали параллелепипеда равны. 4. Диагональным сечением параллелепипеда не может быть… 1) прямоугольник; 2) ромб; 3) трапеция. 5. Не существует тетраэдра, у которого… 1) все грани равные равносторонние треугольники; 2) все грани прямоугольные треугольники; 3) сумма градусных мер углов при одной вершине 360°. 6. Существует параллелепипед, у которого… 1) все углы граней острые; 2) все углы граней прямые; 3) число всех острых углов граней не равно числу всех тупых углов граней. 7. ABCDA1B1C1D1 – параллелепипед. Точки N и Р – середины рёбер AD и CD соответственно, Сечением параллелепипеда плоскостью 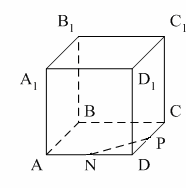 1) BB1; 2) DD1; 3) A1B1. 8. DABC – тетраэдр. Точки M и N – середины рёбер основания АВ и АС соответственно, Сечение тетраэдра плоскостью 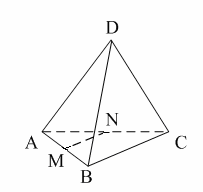 1) ребру AD; 2) ребру BD; 3) грани BCD. Уровень В 1. Треугольник со сторонами 13 см, 12 см и 5 см согнули по его средним линиям и получили модель тетраэдра. Тогда площадь каждой грани тетраэдра равна… 2. В тетраэдре DABC углы DBC, DBA и ABC равны по 60º, DB = AB = BC = 4 см. Тогда площадь грани ADC равна… 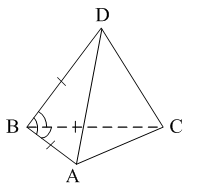 3. В тетраэдре DABC все рёбра равны по 8 см. Точки M, N и K – середины рёбер AD, AB и CB соответственно. Тогда периметр сечения тетраэдра плоскостью MNK равен… 4. Три ребра параллелепипеда равны 3 см, 5 см и 8 см. Тогда сумма длин всех его рёбер равна… Вариант №2 Уровень А 1. ABCD – тетраэдр. Тогда противоположными являются рёбра… 1) AC и ВС; 2) АВ и DC; 3) DB и DC. 2. 6 – это число… 1) вершин тетраэдра; 2) граней тетраэдра; 3) рёбер тетраэдра. 3. Какое предложение неверное? 1) Диагональным сечением параллелепипеда называется сечение параллелепипеда плоскостью, проходящей через его диагонали. 2) Диагональным сечением параллелепипеда является параллелограмм. 3) Диагональные сечения параллелепипеда – равные параллелограммы. 4. Существует параллелепипед, у которого… 1) только одна грань – прямоугольник; 2) только две смежные грани – ромбы; 3) только две противоположные грани – ромбы. 5. Развёрткой тетраэдра является фигура под номером… 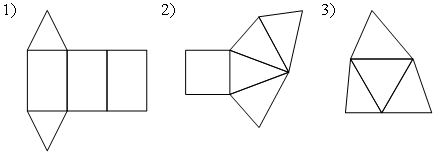 6. Не является развёрткой параллелепипеда фигур под номером… 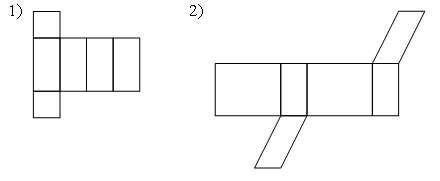 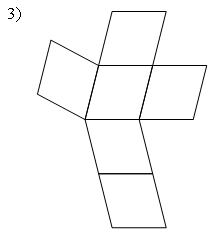 7. ABCDA1B1C1D1 – параллелепипед. Точки M и K – середины рёбер AB и AD соответственно, 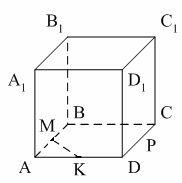 1) СС1; 2) DD1; 3) A1B1 8. DABC – тетраэдр. Точки M и N – середины основания AB и BC соответственно, 1) ребру BD; 2) грани ADC; 3) высоте тетраэдра. 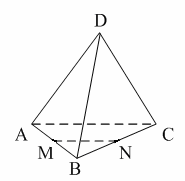 . .Уровень B 1. Треугольник со сторонами 3 см, 4 см и 5 см согнули по его средним линиям и получили модель тетраэдра. Тогда площадь каждой грани тетраэдра равна… 2. В тетраэдре DABC углы DBC, DBA и АВС прямые, DB = AB = BC = 2 см. Тогда площадь грани ADC равна… 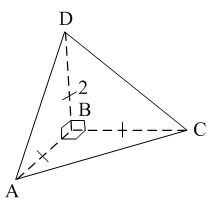 3. Дан тетраэдр DABC, все рёбра которого равны по 4 см. Точки M, N и K – середины рёбер АВ, АС и CD соответственно. Тогда периметр сечения тетраэдра плоскостью MNK равен… 4. Три ребра параллелепипеда равны 3 см, 4 см и 7 см. Тогда сумма длин всех его рёбер равна… тест по теме: « Призма» Вариант №1 Уровень A 1. Призма изображена на рисунке… 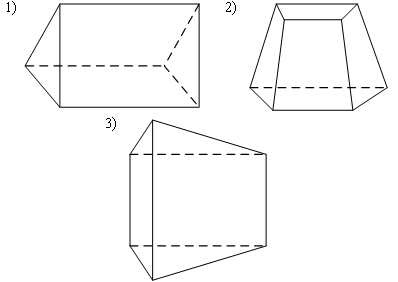 2. 6 – это число… 1) вершин шестиугольной призмы; 2) рёбер треугольной призмы; 3) граней четырёхугольной призмы. 3. Не существует призмы, у которой все грани… 1) ромбы; 2) прямоугольники; 3) треугольники. 4. Существует призма, которая имеет… 1) 13 рёбер; 2) 14 рёбер; 3) 15 рёбер. 5. ABCA1B1C1 – наклонная призма. Тогда СС1B1B не может быть… 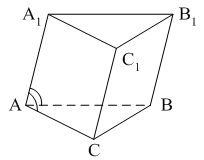 1) ромбом; 2) квадратом; 3) прямоугольником. 6. ABCDA1B1C1D1 – прямой параллелепипед. Тогда ABCD – 1) ромб; 2) квадрат; 3) прямоугольник. 7. Развёрткой наклонной призмы является фигура под номером… 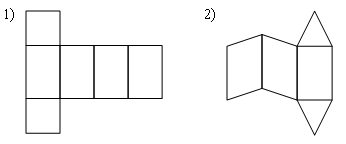 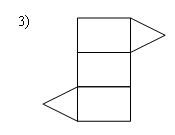 Уровень B 1. В правильной четырёхугольной призме площадь основания равна 144 см2, а высота равна 14 см. Тогда длина диагонали этой призмы… 2. ABCA1B1C1 – правильная призма. A1M = MB1. Тогда 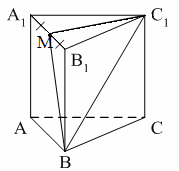 3. ABCA1B1C1 – прямая призма, АА1 = 6 см. АС = 12 см, 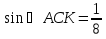 Тогда тангенс угла между плоскостями АВС и А1ВС равен… Вариант №2 Уровень А 1. Призма изображена на рисунке… 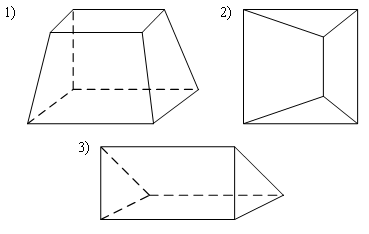 2. 9 – это число… 1) вершин девятиугольной призмы; 2) рёбер треугольной призмы; 3) граней четырёхугольной призмы. 3. Не существует призмы, у которой все грани… 1) ромбы; 2) квадраты; 3) трапеции. 4. Число рёбер призмы кратно… 1) 5; 2) 2; 3) 3 5. ABCDA1B1C1D1 – наклонный параллелепипед. 1) прямоугольник; 2) ромб: 3) квадрат. 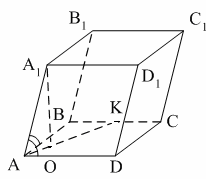 6. ABCA1B1C1 – правильная призма. Тогда угол между BC1 и плоскостью АВВ1 – это…  1) 2) 3) 7. Не является развёрткой правильной призмы фигура под номером… 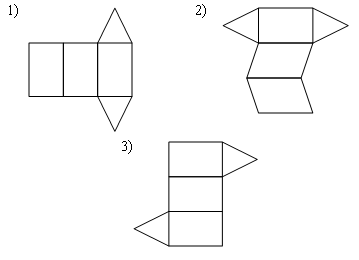 |
