векторы тесты 11 класс. Тесты по геометрии для 11 класса 2013 г. В данной работе представлены тесты по двум разделам Радел 1 включает тему Векторы в пространстве. Метод координат в пространстве
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Уровень В 1. Диагональ основания правильной четырёхугольной призмы равна 8 см, а диагональ боковой грани – 7 см. Тогда диагональ призмы равна… 2. Все рёбра наклонной треугольной призмы равны по 4 см. Боковое ребро АА1 составляет с рёбрами оснований углы по 30°. Тогда площадь боковой поверхности равна… 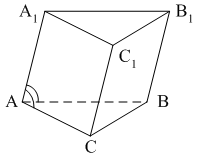 3. ABCDA1B1C1D1 – прямая призма, АА1 = 6 см. ABCD – параллелограмм, Тогда тангенс угла между плоскостями АВС и АВ1С1 равен… 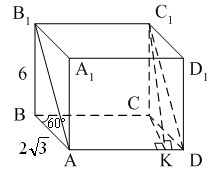 тест по теме: «Пирамида» Вариант №1 Уровень А 1. Многогранник, не являющийся пирамидой, изображён на рисунке… 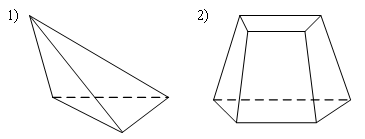 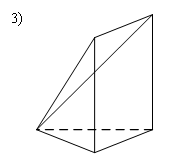 2. 8 – это число… 1) вершин восьмиугольной пирамиды; 2) граней треугольной пирамиды; 3) рёбер четырёхугольной пирамиды. 3. Какое утверждение неверное? 1) Вершина правильной пирамиды проецируется в центр вписанной в основание окружности. 2) Если вершина пирамиды проецируется в центр вписанной в основание окружности, то пирамида правильная. 3) В основании правильной пирамиды лежит правильный n-угольник. 4. Неверно, что… 1) апофема – это высота боковой грани; 2) апофема не может совпадать с высотой пирамиды; 3) апофемы всех боковых граней пирамиды равны. 5. Не существует четырёхугольной пирамиды, у которой… 1) все боковые грани – равные равнобедренные прямоугольные треугольники; 2) все грани – равносторонние треугольники; 3) противоположные боковые грани перпендикулярны плоскости основания. 6. Если вершина пирамиды проецируется в центр описанной около основания окружности, то равны… 1) апофемы; 2) углы наклона боковых рёбер к плоскости основания; 3) двугранные углы при рёбрах основания. 7. Если вершина пирамиды проецируется в центр вписанной в основание окружности, то равны… 1) апофемы; 2) боковые рёбра; 3) углы наклона боковых рёбер к плоскости основания. 8. FABCD – пирамида, 1) ромбом; 2) квадратом; 3) прямоугольником. Уровень В 1. Боковые рёбра треугольной пирамиды равны 3 см, 4 см и 7 см. Одно из них перпендикулярно плоскости основания. Тогда высота пирамиды равна… 2. В основании пирамиды, которая имеет 32 ребра, лежит… 3. DABC – пирамида, 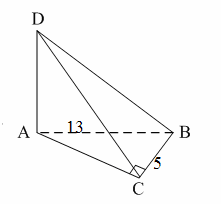 4. DABC – пирамида, Тогда длина наибольшего ребра равна… 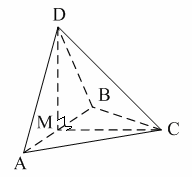 тест по теме: «Пирамида» Вариант №2 Уровень А 1. Пирамида изображена на рисунке… 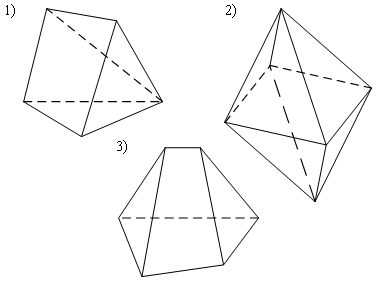 2. 6 – это число… 1) вершин шестиугольной пирамиды; 2) рёбер треугольной пирамиды; 3) граней четырёхугольной пирамиды. 3. Какое утверждение неверное? 1) В основании правильной пирамиды лежит правильный n-угольник. 2) Если в основании пирамиды лежит правильный n-угольник, то пирамида правильная. 3) Вершина правильной пирамиды проецируется в центр описанной около основания окружности. 4. По формуле 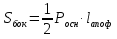 можно найти площадь боковой поверхности пирамиды, изображённой на рисунке… можно найти площадь боковой поверхности пирамиды, изображённой на рисунке…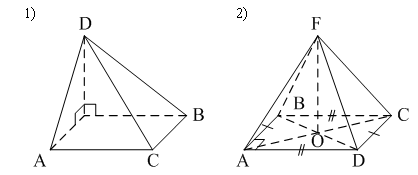 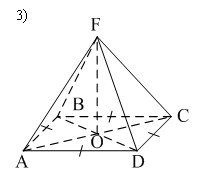 5. Число рёбер пирамиды кратно… 1) 5; 2) 2; 3) 3. 6. Если вершина пирамиды проецируется в центр описанной около основания окружности, то равны… 1) апофемы; 2) боковые рёбра; 3) двугранные углы при рёбрах основания. 7. Если вершина пирамиды проецируется в центр вписанной в основание окружности, то равны… 1) боковые рёбра; 2) углы наклона боковых рёбер к плоскости основания; 3) двугранные углы при рёбрах основания. 8. FABCD – пирамида. Тогда ABCD не может быть… 1) ромбом; 2) квадратом; 3) прямоугольником. Уровень В 1. Боковые рёбра треугольной пирамиды равны 5 см, 12 см и 7 см. Одно из них перпендикулярно плоскости основания. Тогда высота пирамиды равна… 2. Основанием пирамиды, имеющей 20 рёбер, является… 3. FABCD – пирамида, Тогда высота пирамиды равна… 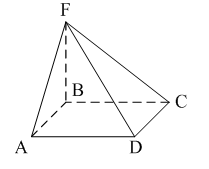 4. DABC – пирамида, Треугольники АВС и ABD равносторонние. Длина наибольшего ребра равна Тогда длина ребра основания равна… 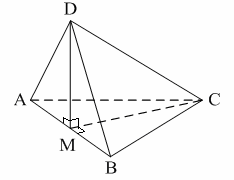 тест по теме: «Цилиндр» Вариант №1 1. Цилиндр нельзя получить вращением… 1) треугольника вокруг одной из сторон; 2) квадрата вокруг одной из сторон; 3) прямоугольника вокруг одной из сторон. 2. Площадь боковой поверхности цилиндра можно вычислить по формуле… 1) 2) 3) 3. Сечением цилиндра плоскостью, перпендикулярной его образующей, является… 1) круг; 2) прямоугольник; 3) трапеция. 4. На основаниях цилиндра взяты две параллельные друг другу хорды, проходящие через центры оснований. Тогда расстояние между хордами… 1) равно высоте цилиндра; 2) больше высоты цилиндра; 3) меньше высоты цилиндра. 5. Боковой поверхностью цилиндра высотой H и диаметром основания d является квадрат. Тогда верно, что… 1) d = H; 2) 3) 6. Развёрткой боковой поверхности прямого кругового цилиндра может быть… 1) прямоугольник; 2) ромб; 3) параллелограмм. 7. Отношение площадей боковой поверхности и осевого сечения цилиндра равно… 1) 2) 3) 8. Площадь боковой поверхности цилиндра в 2 раза больше площади основания. Тогда отношение 1) 1; 2) 2; 3) 3. тест по теме: «Цилиндр» Вариант №2 1. Цилиндр можно получить вращением… 1) трапеции вокруг одного из оснований; 2) ромба вокруг одной из диагоналей; 3) прямоугольника вокруг одной из сторон. 2. Площадь боковой поверхности цилиндра нельзя вычислить по формуле… 1) 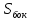 = =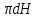 2) 3) 3. Сечением цилиндра плоскостью, параллельной его образующей, является… 1) круг; 2) прямоугольник; 3) трапеция. 4. На основаниях цилиндра взяты две перпендикулярные друг другу хорды, проходящие через центры оснований. Тогда расстояние между хордами… 1) равно образующей цилиндра; 2) больше высоты цилиндра; 3) меньше образующей цилиндра. 5. Боковой поверхностью цилиндра с высотой H и радиусом основания R является квадрат. Тогда верно, что… 1) 2) 3) 6. Развёрткой боковой поверхности прямого кругового цилиндра не может быть… 1) прямоугольник; 2) ромб; 3) квадрат. 7. Площадь боковой поверхности цилиндра больше площади осевого сечения цилиндра в… 1) 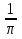 раз; раз; 2) 2 раза; 3) 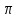 раз. раз.8. Площадь боковой поверхности цилиндра в 3 раза больше площади основания. Тогда отношение 1) 1; 2) 1,5; 3) 3. тест по теме: «Конус» Вариант №1 1. Конус может быть получен вращением… 1) равностороннего треугольника вокруг его стороны; 2) прямоугольного треугольника вокруг одного из его катетов; 3) прямоугольного треугольника вокруг гипотенузы. 2. Площадь боковой поверхности конуса можно вычислить по формуле… 1) 3. Сечением конуса плоскостью, перпендикулярной оси цилиндра, является… 1) треугольник; 2) прямоугольник; 3) круг. 4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка… 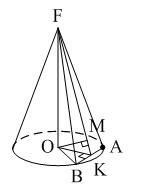 1) OB; 2) OK; 3) OM. 5. Развёрткой боковой поверхности конуса является круговой… 1) сегмент; 2) сектор; 3) слой. 6. Площадь полной поверхности конуса равна… 1) 7. Наибольший периметр имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в… 1) 60°; 2) 90°; 3) 180°. 8. Через вершину конуса и хорду ВС проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания это угол… 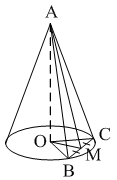 1) ABO; 2) AMO; 3) BAC. тест по теме: «Конус» Вариант №2 1. Конус может быть получен вращением… 1) прямоугольного треугольника вокруг гипотенузы; 2) равнобедренного треугольника вокруг медианы, проведённой к основанию; 3) тупоугольного треугольника вокруг одной из его сторон. 2. Площадь боковой поверхности конуса нельзя вычислить по формуле… 1) 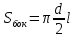 3. Сечением конуса плоскостью, проходящей вершину конуса и хорду основания, не может быть… 1) прямоугольный треугольник; 2) равнобедренный треугольник; 3) разносторонний треугольник. 4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка… 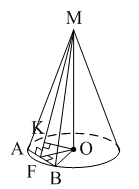 1) OF; 2) OK; 3) OB. 5. а – образующая конуса, b – высота конуса. Тогда верно, что… 1) a > b; 2) a = b; 3) a < b. 6. Площадь полной поверхности конуса, у которого осевым сечением является равносторонний треугольник со стороной а, равна… 1) 7. Наибольшую площадь имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в… 1) 60°; 2) 90°; 3) 180°. 8. Через вершину конуса и хорду AB проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания – это угол… 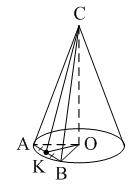 1) ACB; 2) OAC; 3) CKO. Источники информации: 1.Изучение геометрии в 10-11 классах: кн. для учителя /С.М.Саакян, В.Ф.Бутузов.- 4-е изд., дораб.- М.: Просвещение. 2010. 2. «Геометрия 10-11» Учебник для общеобразовательных учреждений. Л. С. Атанасян, И. Ф. Бутузов, С. Б. Кодомцев и др. М.: Просвещение.2010. 3.ЕГЭ 2012. Математика. Задача В9. Стереометрия: расстояние в пространстве. Рабочая тетрадь / Под ред. А.Л.Семенова и И.В.Ященко.-М.: МЦНМО, 2012. 4. ЕГЭ 2012. Математика. Задача В9. Стереометрия: объемы и площади. Рабочая тетрадь / Под ред. А.Л.Семенова и И.В.Ященко.-М.: МЦНМО, 2012. 5.Геометрия 7-11 классы. Практикум. Издательство «Учитель».Волгоград.2010. |
