Задача по физике. Задача. Решение Вычислим поток электрического поля через площадь поверхности цилиндра. Полный поток складывается из потока через боковую поверхность цилиндра и потока через основания
 Скачать 151.75 Kb. Скачать 151.75 Kb.
|
|
Полый стеклянный цилиндр равномерно заряжен с объемной плотностью ρ=0,1 мКл/м3. Внешний радиус цилиндра равен 2 см, внутренний 0,75 см. Используя теорему Остроградского-Гаусса, найдите зависимость модуля вектора напряженности Е и электрического смещения D от расстояния до оси цилиндра. Постройте графики зависимостей E(r, D(r). Диэлектрическая проницаемость стекла равна 5.
В области от 0 до r зарядов внутри нет, тогда  Если  , тогда из заряда стеклянного цилиндра вырезается лишь часть заряда q и полость, где плотность зарядов равна нулю, представим как наложение цилиндра с объемным зарядом –𝞺 на сплошной цилиндр с объемным зарядом +𝞺. Поэтому, заряд внутри поверхности Гаусса равен , тогда из заряда стеклянного цилиндра вырезается лишь часть заряда q и полость, где плотность зарядов равна нулю, представим как наложение цилиндра с объемным зарядом –𝞺 на сплошной цилиндр с объемным зарядом +𝞺. Поэтому, заряд внутри поверхности Гаусса равен 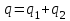  , ,   где h – высота цилиндрической замкнутой поверхности. Площадь боковой поверхности цилиндра:  . .Следовательно, поток вектора  через эту замкнутую боковую поверхность будет равен через эту замкнутую боковую поверхность будет равен 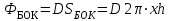 . .  Если  , тогда полость, где плотность зарядов равна нулю, представим как наложение цилиндра с объемным зарядом –𝞺 на сплошной цилиндр с объемным зарядом +𝞺. Поэтому, заряд внутри поверхности Гаусса равен , тогда полость, где плотность зарядов равна нулю, представим как наложение цилиндра с объемным зарядом –𝞺 на сплошной цилиндр с объемным зарядом +𝞺. Поэтому, заряд внутри поверхности Гаусса равен 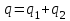 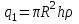 , ,   Площадь боковой поверхности цилиндра:  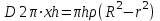 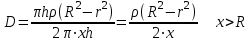 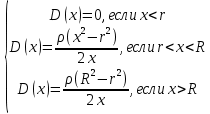 Воспользуемся теперь связью векторов D и E:    Построим график зависимости D (r), для этого исследуем поведение функции. В точке  ( ( стремится к стремится к  слева) смещение слева) смещение  . . стремится к стремится к 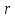 справа) смещение справа) смещение 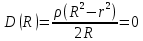 . Следовательно, функция D (𝑥) разрыва не имеет. . Следовательно, функция D (𝑥) разрыва не имеет.В точке  ( ( стремится к стремится к  слева) напряженность слева) напряженность  . .В точке  ( ( стремится к стремится к 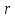 справа) напряженность справа) напряженность  . Следовательно, функция Е (𝑥) разрыв имеет. . Следовательно, функция Е (𝑥) разрыв имеет.Подставим числа:  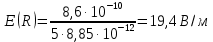 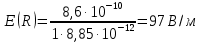  Ответ:  |








 0.
0.