Тесты по курсу «Теория вероятностей и математическая статистика» I. "Элементы теории вероятностей" Тест 1.1. В каких пределах заключена вероятность появления случайного события?
a) любое число от 0 до 1 б) любое положительное число
в) любое неотрицательное число г) любое число от -1 до 1
Тест 1.2. Чему равна вероятность достоверного события?
а) 0,5 б) 0 в) 1 г) 0,25
Тест 1.3. Чему равна вероятность невозможного события?
а) 0,5 б) 0 в) 1 г) 0,25
Тест 1.4. Если два события не могут произойти одновременно, то они называются:
а) невозможными б) совместными в) независимыми г) несовместными
Тест 1.5. Если два события могут произойти одновременно, то они называются:
а) зависимыми б) совместными в) независимыми г) несовместными
Тест 1.6. Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет король пик?
а) 1/52 б) 1/4 в) 1/13 г) 1/52!
Тест 1.7. Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет король?
а) 1/52 б) 1/4 в) 1/13 г) 4!/52!
Тест 1.8. Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет карта пиковой масти?
а) 1/52 б) 1/4 в) 1/13 г) 13!/52!
Тест 1.9. Монета была подброшена 10 раз. “Герб” выпал 4 раза. Какова относительная частота выпадения “герба”?
а) 0 б) 0,4 в) 0,5 г) 0,6
Тест 1.10. Консультационный пункт университета получает пакеты с контрольными работами студентов из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В — 0,2. Какова вероятность того, что очередной пакет будет получен из города С?
а) 0,14 б) 0,1 в) 0,86 г) 0,9
Тест 1.11. Какие основные числовые характеристики дают представление об одномерной случайной величине?
а) математическое ожидание и дисперсия б) математическое ожидание
в) дисперсия г) нет правильных ответов
Тест 1.12. Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна 0,2. Для второго клиента вероятность такого обращения равна 0,1. Найти вероятность того, что в течение года в страховую компанию не обратится ни один клиент, если обращения клиентов — события независимые.
а) 0,02 б) 0,72 в) 0,3 г) 0,98
Тест 1.13. Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна 0.2. Для второго клиента вероятность такого обращения равна 0.3. Найти вероятность того, что в течение года в СК обратится хотя бы один клиент, если обращения клиентов — события независимые.
а) 0,56 б) 0,44 в) 0,8 г) 0,06
Тест 1.14. В магазин поступают телевизоры с трех заводов: 30% — с первого завода, 25% — со второго, остальные с третьего. Какова вероятность случайного выбора телевизора с третьего завода?
а) 0,45 б) 0,55 в) 0,25 г) 0,35
Тест 1.15. Чему равно математическое ожидание постоянной величины?
а) 0 б) 1 в) этой величине г) квадрату этой величины
Тест 1.16. Чему равна дисперсия постоянной величины?
а) 0 б) 1 в) этой величине г) квадрату этой величины
Тест 1.17. Чему равна дисперсия случайной величины Y=3X+5, если дисперсия X равна 2?
а) 18 б) 6 в) 11 г) 23
Тест 1.18. Чему равно математическое ожидание случайной величины Y=4X+2, если математическое ожидание X равно 3?
а) 14 б) 3 в) 18 г) 12
Тест 1.19. Как называются два события, сумма которых есть событие достоверное, а произведение — событие невозможное?
а) противоположные б) несовместные в) равносильные г) совместные
Тест 1.20. Отношением числа случаев, благоприятствующих событию A, к числу всех возможных случаев называется...
а) вероятность б) математическое ожидание в) число сочетаний г) число размещений
Тест 1.21. Бросают игральный кубик. Найдите вероятность выпадения грани с 6 очками:
а) 1/9 б) 1/6 в) 1/2 г) 1/36
Тест 1.22. Бросают игральный кубик. Найдите вероятность выпадения грани с нечётным числом очков:
а) 1/3 б) 1/2 в) 1/4 г) 1/6
Тест 1.23. Бросают игральный кубик. Найдите вероятность выпадения грани с 1 или 3:
а) 1/3 б) 1/2 в) 1/4 г) 1/6
Тест 1.24. Бросают игральный кубик. Найдите вероятность выпадения грани с чётным числом очков:
а) 5/6 б) 1/2 в) 1/6 г) 2/6
Тест 1.25. В урне 2 белых и 3 черных шара. Вынимают шар. Найти вероятность того, что этот шар — белый
а) 1/2 б) 1/5 в) 4/25 г) 2/5
Тест 1.26. В урне 2 белых и 3 черных шара. Подряд вынимают два шара, при этом каждый раз шары возвращают обратно в корзину. Найти вероятность того, что оба вынутых шара — белые.
а) 1/10 б) 1/5 в) 4/25 г) 2/5
Тест 1.27. В урне 2 белых и 3 черных шара. Подряд вынимают два шара, при этом шары не возвращают обратно в корзину. Найти вероятность того, что оба вынутых шара — белые.
а) 2/20 б) 1/5 в) 4/25 г) 2/5
Тест 1.28. В коробке 12 стандартных и 3 бракованных детали. Вынимают 1 деталь. Найти вероятность того, что эта деталь — бракованная.
а) 1/3 б) 1/15 в) 12/15 г) 3/15
Тест 1.29. В коробке 12 стандартных и 3 бракованных детали. Вынимают 1 деталь. Найти вероятность того, что эта деталь — стандартная.
а) 1/3 б) 1/15 в) 12/15 г) 3/15
Тест 1.30. В коробке 4 стандартных и 2 бракованных детали. Подряд вынимают две детали, при этом не возвращают их обратно в коробку. Найти вероятность того, что обе вынутые детали — бракованные.
а) 2/6 б) 4/36 в) 2/30 г) 1/3
Тест 1.31. В коробке 4 стандартных и 2 бракованных детали. Последовательно по одной вынимают две детали, при этом каждый раз возвращают их обратно в коробку. Найти вероятность того, что обе вынутые детали — бракованные.
а) 2/6 б) 4/36 в) 2/30 г) 1/3
Тест 1.32. Какова вероятность выпадения «орла» при подбрасывании монеты?
а) 1/2 б) 0,33 в) 0,1 г) 0,25
Тест 1.33. В связке 10 похожих ключей от сейфов. Определите вероятность, с которой первыми наугад выбранными ключами можно открыть сейф с двумя последовательно открывающимися замками.
а) 1/10 б) 1/90 в) 2/10 г) 1/100
Тест 1.34. Сколько различных трёхбуквенных комбинаций можно составить из букв К, Н, И, Г, А?
а) 20 б) 60 в) 30 г) 10
Тест 1.35. Сколько различных двухбуквенных комбинаций можно составить из букв К, Н, И, Г, А?
а) 60 б) 20 в) 40 г) 5
Тест 1.36. Некто забыл последние две цифры номера телефона своего знакомого и, помня лишь, что они различны, пытается набрать номер наугад. Какова вероятность, что он дозвонится с первого раза?
а) 1/10 б) 1/90 в) 2/10 г) 1/100
Тест 1.37. Сколькими способами можно поставить 5 человек в очередь?
а) 25 б) 120 в) 5 г) 100
Тест 1.38. Чему равно математическое ожидание суммы случайных величин?
а) 0
б) 1
в) сумме их математических ожиданий
г) произведению их математических ожиданий
Тест 1.39. Какое событие называется случайным?
а) событие, которое должно либо произойти, либо не произойти при выполнении некоторого комплекса условий
б) событие, которое вряд ли произойдет
в) событие, которое произойдет, но не скоро
г) событие, которое неожиданно произошло
Тест 1.40. Если событие не происходит ни при каком испытании, то оно называется:
а) невозможным б) достоверным в) случайным г) независимым
Тест 1.41. Если событие обязательно происходит при каждом испытании, то оно называется:
а) невозможным б) достоверным в) случайным г) независимым
Тест 1.42. Два события называют несовместимыми, если:
а) они должны произойти при каждом испытании
б) они могут произойти одновременно в результате испытания
в) их совместное наступление в результате испытания невозможно
г) все ответы верны
Тест 1.43. Два события называют совместимыми, если:
а) они должны произойти при каждом испытании
б) они могут произойти одновременно в результате испытания
в) их совместное наступление невозможно
г) все ответы верны
Тест 1.44. Если все значения случайной величины увеличить на какое-то число, как изменится её математическое ожидание?
а) не изменится б) увеличится на это число
в) уменьшится на это число г) увеличится в это число раз
Тест 1.45. Чему равно математическое ожидание произведения независимых случайных величин?
а) 0
б) 1
в) сумме математических ожиданий
г) произведению математических ожиданий
Тест 1.46. Постоянную величину вынести за знак дисперсии:
а) нельзя
б) можно, при этом извлечь из нее корень
в) можно, умножив при этом на n
г) можно, возведя при этом в квадрат
Тест 1.47. При вынесении постоянной величины за знак математического ожидания эту величину:
а) возводят в квадрат
б) извлекают из данной величины квадратный корень
в) умножают на n
г) просто выносят за скобки
Тест 1.48. При вынесении постоянной величины за знак дисперсии эту величину:
а) возводят в квадрат
б) извлекают из данной величины квадратный корень
в) умножают на n
г) просто выносят за скобки
Тест 1.49. Если вероятность наступления одного события зависит от того, произошло ли другое событие, то они называются:
а) зависимыми б) совместными в) независимыми г) несовместными
Тест 1.50. Если вероятность наступления одного события не зависит от того, произошло ли другое событие, то они называются:
а) независимыми б) совместными в) зависимыми г) несовместными
Тест 1.51. Как называются два события, непоявление одного из которых влечёт появление другого?
а) противоположные б) несовместные в) равносильные г) совместные
Тест 1.52. Как изменится дисперсия случайной величины, если все её возможные значения увеличить на какое-то число?
а) не изменится б) увеличится на это число
в) уменьшится на это число г) увеличится в это число раз
Тест 1.53. Какие из этих элементов комбинаторики представляют собой неупорядоченные подмножества (порядок следования элементов в которых не важен)?
а) число размещений с повторениями б) число размещений
в) число сочетаний г) число перестановок
Тест 1.54. У какого распределения случайной величины вероятности рассчитываются по формуле Бернулли?
а) пуассоновского б) нормального в) биномиального г) равномерного
Тест 1.55. Какое из нижеуказанных распределений случайной величины является непрерывным?
а) пуассоновское б) геометрическое в) биномиальное г) равномерное
Тест 1.56. Какое из нижеуказанных распределений случайной величины является дискретным?
а) показательное б) нормальное в) биномиальное г) равномерное
Тест 1.57. Как иначе называют функцию плотности вероятности любой непрерывной случайной величины?
а) интегральная функция б) дифференциальная функция
в) функция Лапласа г) функция Гаусса
Тест 1.58. Как иначе называют функцию распределения любой непрерывной случайной величины?
а) интегральная функция б) дифференциальная функция
в) функция Лапласа г) функция Гаусса
Тест 1.59. Какая функция используется в интегральной теореме Муавра-Лапласа?
а) интегральная функция б) дифференциальная функция
в) функция Лапласа г) функция Гаусса
Тест 1.60. Какая функция используется в локальной теореме Муавра-Лапласа?
а) интегральная функция б) дифференциальная функция
в) функция Лапласа г) функция Гаусса
Тест 1.61. В задачах на расчёт вероятности того, что в n независимых испытаниях событие А появится ровно m раз, используется при малом числе испытаний:
а) локальная теорема Муавра-Лапласа б) формула Пуассона
в) интегральная теорема Муавра-Лапласа г) формула Бернулли
Тест 1.62. В задачах на расчёт вероятности того, что в n независимых испытаниях событие A появится ровно m раз, используется при большом числе испытаний и малой вероятности p:
а) локальная теорема Муавра-Лапласа б) формула Пуассона
в) интегральная теорема Муавра-Лапласа г) формула Бернулли
Тест 1.63. В задачах на расчёт вероятности того, что в n независимых испытаниях событие А появится ровно m раз, используется при большом числе испытаний и вероятности p, отличной от 0 и 1:
а) локальная теорема Муавра-Лапласа б) формула Пуассона
в) интегральная теорема Муавра-Лапласа г) формула Бернулли
Тест 1.64. В задачах на расчёт вероятности того, что в n независимых испытаниях событие A появится от a до b раз, используется при большом числе испытаний и вероятности p, отличной от 0 и 1:
а) локальная теорема Муавра-Лапласа б) формула Пуассона
в) интегральная теорема Муавра-Лапласа г) формула Бернулли
Тест 1.65. Интеграл в бесконечных пределах от плотности непрерывной случайной величины равен:
а) 0 б) любому числу от 0 до 1 в) 1 г) положительному числу
Тест 1.66. Какие значения может принимать плотность непрерывной случайной величины:
а) любые неотрицательные значения б) от 0 до 1
в) любые положительные значения г) от -1 до 1
Тест 1.67. Какие значения может принимать функция распределения случайной величины:
а) любые неотрицательные значения б) от 0 до 1
в) любые положительные значения г) от -1 до 1
Тест 1.68. Функция распределения любой случайной величины есть функция:
а) неубывающая б) убывающая в) невозрастающая г) возрастающая
Тест 1.69. Плотность непрерывной случайной величины есть … её функции распределения
а) производная б) первообразная в) функция Лапласа г) функция Гаусса
Тест 1.70. Функция распределения непрерывной случайной величины есть … её плотности
а) производная б) первообразная в) функция Лапласа г) функция Гаусса
II. "Статистическая оценка параметров распределения" Тест 2.1. Известен доход по 4 фирмам Х1=10, Х2=15, Х3=18, Х4=12. Известна также выборочная средняя по 5 фирмам, равная 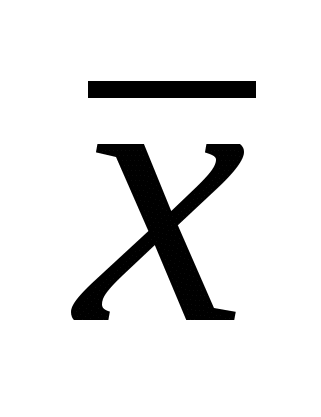 =15. Доход пятой фирмы равен =15. Доход пятой фирмы равен
а) 25 б) 10 в) 15 г) 20
Тест 2.2. Что является оценкой математического ожидания?
а) выборочная средняя 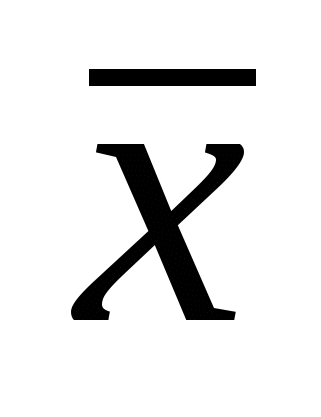 б) выборочная дисперсия s2 б) выборочная дисперсия s2
в) относительная частота m/n г) исправленная выборочная дисперсия 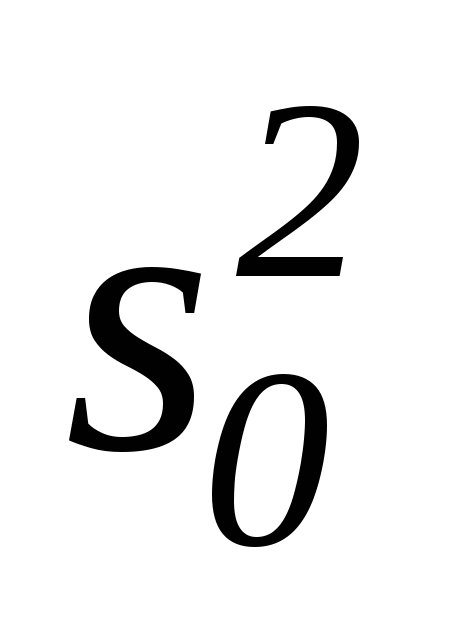
Тест 2.3. Что является оценкой генеральной дисперсии?
а) выборочная средняя 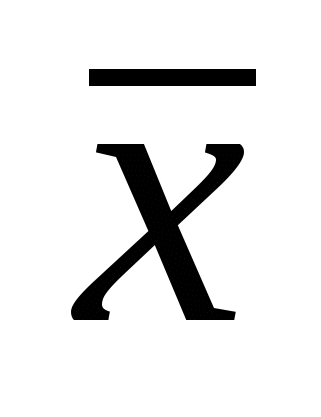 б) выборочная дисперсия s2 б) выборочная дисперсия s2
в) относительная частота m/n г) генеральная средняя μ
Тест 2.4. Что является несмещённой оценкой генеральной дисперсии?
а) выборочная средняя 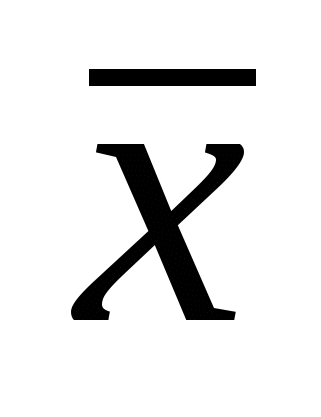 б) выборочная дисперсия s2 б) выборочная дисперсия s2
в) относительная частота m/n г) исправленная выборочная дисперсия 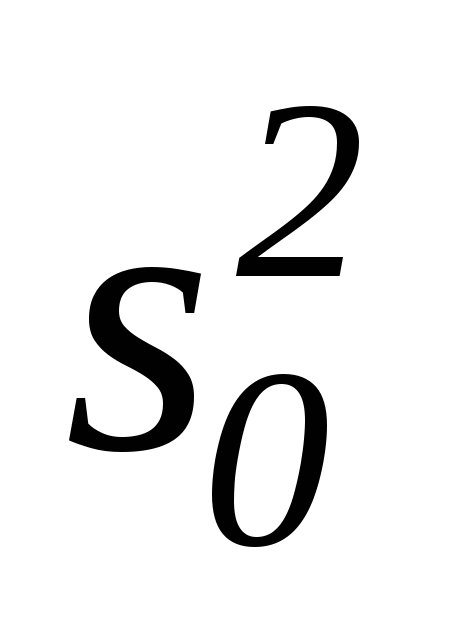
Тест 2.5. Каким выборочным моментом является выборочная дисперсия s2?
а) выборочным центральным моментом 1-го порядка
б) выборочным начальным моментом 1-го порядка
в) выборочным начальным моментом 2-го порядка
г) выборочным центральным моментом 2-го порядка
Тест 2.6. Каким выборочным моментом является выборочная средняя 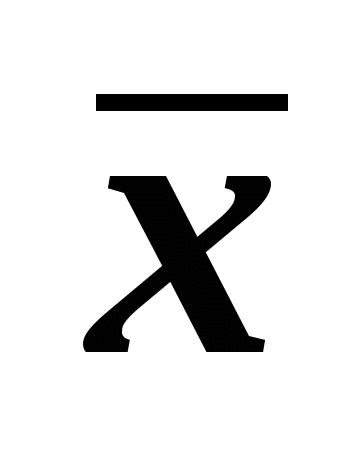 ? ?
а) выборочным центральным моментом 1-го порядка
б) выборочным начальным моментом 1-го порядка
в) выборочным начальным моментом 2-го порядка
г) выборочным центральным моментом 2-го порядка
Тест 2.7. Что является оценкой генеральной доли (вероятности)?
а) выборочная средняя 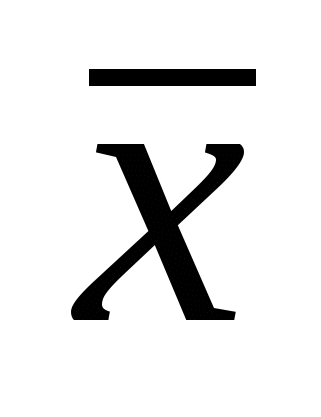 б) выборочная дисперсия s2 б) выборочная дисперсия s2
в) относительная частота m/n г) исправленная выборочная дисперсия 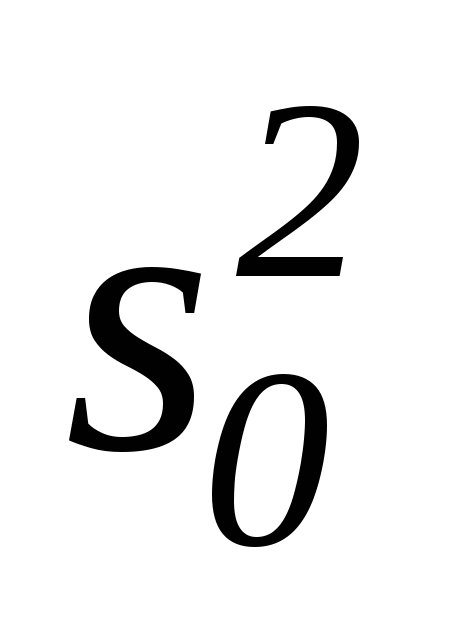
Тест 2.8. Если математическое ожидание оценки при любом объёме выборки равно оцениваемому параметру, то точечная оценка называется:
а) состоятельной б) эффективной в) несмещенной г) все ответы верны
Тест 2.9. Если точечная оценка параметра при увеличении объёма выборки сходится по вероятности к оцениваемому параметру, то точечная оценка называется:
а) состоятельной б) эффективной в) несмещенной г) все ответы верны
Тест 2.10. Точечную оценку называют эффективной, если она:
а) обладает минимальной дисперсией среди всех несмещенных оценок
б) обладает максимальной дисперсией среди всех несмещенных оценок
в) сходится по вероятности к оцениваемому параметру
г) нет правильного ответа
Тест 2.11. Чему равна сумма доверительной вероятности и уровня значимости γ+α?
а) 1 б) неотрицательному числу в) 0 г) какому-то числу от 0 до 1
Тест 2.12. Симметричный ли интервал строится при оценивании генеральной средней?
а) нет б) зависит от изучаемого явления в) да г) нет правильного ответа
Тест 2.13. Симметричный ли интервал строится при оценивании генеральной доли?
а) нет б) зависит от изучаемого явления в) да г) нет правильного ответа
Тест 2.14. При построении доверительного интервала для генеральной дисперсии при малых объёмах выборки используют
а) распределение Пирсона б) нормальный закон распределения
в) распределение Фишера-Снедекора г) распределение Стьюдента
Тест 2.15. При построении доверительного интервала для генеральной дисперсии при больших объёмах выборки используют
а) распределение Пирсона б) нормальный закон распределения
в) распределение Фишера-Снедекора г) распределение Стьюдента
Тест 2.16. При построении доверительного интервала для генеральной доли или вероятности при больших объёмах выборки используют
а) распределение Пирсона б) нормальный закон распределения
в) распределение Фишера-Снедекора г) распределение Стьюдента
Тест 2.17. Выборкой называют множество результатов наблюдений, отобранных
а) по определенному критерию б) по определённому правилу
в) случайно г) нет правильного ответа
Тест 2.18. Выборка репрезентативна. Это означает, что:
а) она неправильно отражает основные свойства генеральной совокупности
б) она правильно отражает основные свойства генеральной совокупности
в) ее объем превышает 30 наблюдений
г) нет правильного ответа
Тест 2.19. Чем достигается репрезентативность выборки?
а) подбором наблюдений б) случайностью отбора
в) объёмом г) нет правильного ответа
Тест 2.20. Если случайная величина распределена по нормальному закону, то выборочная средняя 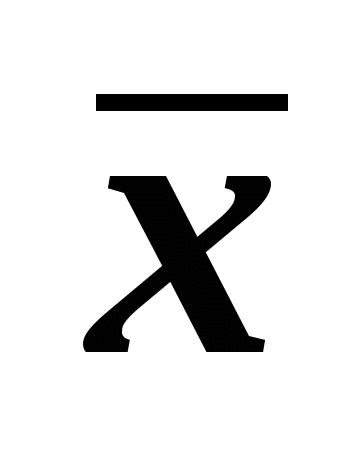 распределена распределена
а) по биномиальному закону б) по нормальному закону
в) не имеет определённого закона распределения г) по закону Пуассона
Тест 2.21. При интервальном оценивании математического ожидания при неизвестном значении генеральной дисперсии используют
а) распределение Стьюдента б) нормальное распределение
в) распределение Фишера-Снедекора г) распределение Пирсона
Тест 2.22. При интервальном оценивании математического ожидания при известном значении генеральной дисперсии используют
а) распределение Стьюдента б) нормальное распределение
в) распределение Фишера-Снедекора г) распределение Пирсона
Тест 2.23. Перечислите основные свойства точечных оценок:
а) несмещенность и эффективность б) эффективность и состоятельность
в) несмещенность, эффективность и состоятельность г) несмещенность и состоятельность
Тест 2.24. В теории статистического оценивания оценки бывают:
а) только интервальные б) только точечные
в) точечные и интервальные г) нет правильного ответа
Тест 2.25. Ширина доверительного интервала зависит от:
а) уровня значимости и числа наблюдений б) уровня значимости
в) числа наблюдений г) нет правильного ответа
Тест 2.26. От чего зависит число степеней свободы в распределении Стьюдента?
а) от доверительной вероятности б) от объёма выборки
в) от доверительной вероятности и объёма выборки г) от значения выборочной дисперсии
Тест 2.27. От чего зависит точность оценивания генеральной средней при построении доверительного интервала в случае неизвестной генеральной дисперсии?
а) от доверительной вероятности б) от объёма выборки
в) от доверительной вероятности, выборочной дисперсии и объёма выборки
г) от доверительной вероятности, генеральной дисперсии и объёма выборки
Тест 2.28. От чего зависит точность оценивания генеральной средней при построении доверительного интервала в случае известной генеральной дисперсии?
а) от доверительной вероятности б) от объёма выборки
в) от доверительной вероятности, выборочной дисперсии и объёма выборки
г) от доверительной вероятности, генеральной дисперсии и объёма выборки
Тест 2.29. От чего зависит точность оценивания генеральной доли или вероятности при построении доверительного интервала в случае большого объёма выборки?
а) от доверительной вероятности б) от объёма выборки
в) от доверительной вероятности, частности и объёма выборки
г) от доверительной вероятности, выборочной дисперсии и объёма выборки
Тест 2.30. Что является центром при построении доверительного интервала для генеральной средней?
а) выборочная средняя 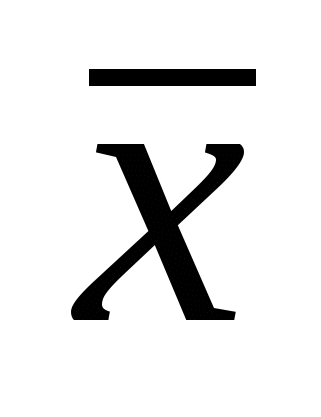 б) выборочная дисперсия s2 б) выборочная дисперсия s2
в) относительная частота m/n г) исправленная выборочная дисперсия 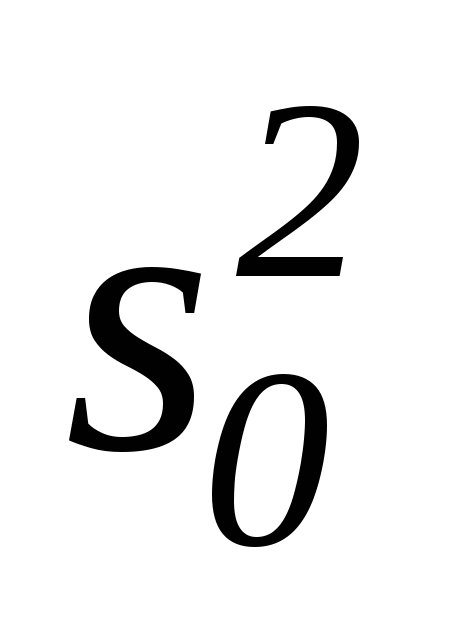
Тест 2.31. Что является центром при построении доверительного интервала для генеральной доли или вероятности?
в) относительная частота m/n г) исправленная выборочная дисперсия 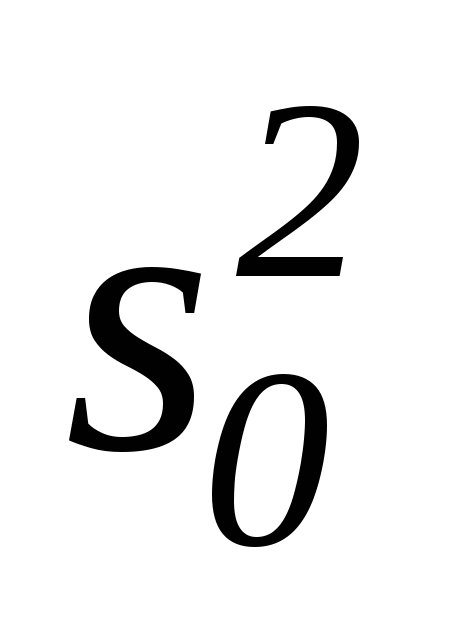
в) относительная частота m/n г) исправленная выборочная дисперсия 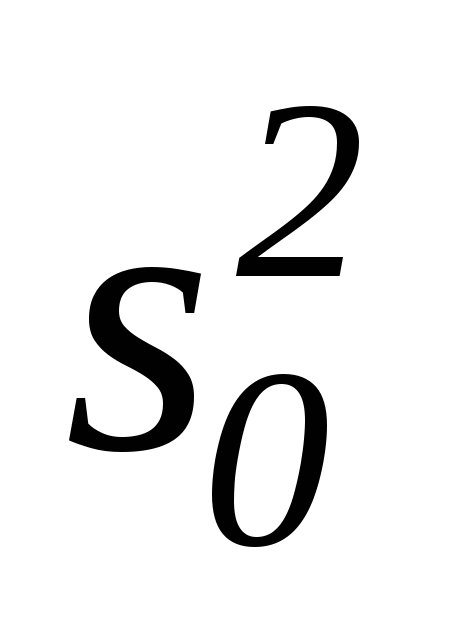
Тест 2.32. Симметричный ли интервал строится при оценивании генеральной дисперсии?
а) нет б) зависит от изучаемого явления в) да г) нет правильного ответа
Тест 2.33. При построении доверительного интервала для генеральной доли или вероятности при малых объёмах выборки используют
а) распределение Пирсона б) нормальный закон распределения
в) формулу Бернулли г) распределение Стьюдента
III. "Проверка статистических гипотез" Тест 3.1. Статистической гипотезой называют предположение:
а) о виде или параметрах неизвестного закона распределения случайной величины
б) о равенстве двух параметров
в) о неравенстве двух величин
г) нет правильного ответа
Тест 3.2. Простой называют статистическую гипотезу:
а) не определяющую однозначно закон распределения
б) однозначно определяющую закон распределения
в) определяющую несколько параметров распределения
г) определяющую один параметр распределения
Тест 3.3. Сложной называют статистическую гипотезу:
а) не определяющую однозначно закон распределения
б) однозначно определяющую закон распределения
в) определяющую несколько параметров распределения
г) определяющую один параметр распределения
Тест 3.4. Нулевая гипотеза — это:
а) выдвинутая гипотеза, которую нужно проверить
б) альтернативная гипотеза
в) гипотеза, определяющая закон распределения
г) гипотеза о равенстве нулю параметра распределения
Тест 3.5. Конкурирующая гипотеза — это:
а) выдвинутая гипотеза, которую нужно проверить
б) гипотеза, определяющая закон распределения
в) гипотеза, противоположная нулевой
г) гипотеза о неравенстве нулю параметра распределения
Тест 3.6. Статистическим критерием называют:
а) правило, устанавливающее условия, при которых проверяемую гипотезу следует либо отвергнуть, либо не отвергнуть
б) правило, устанавливающее условия, при которых проверяемая гипотеза верна
в) правило, устанавливающее условия, при которых проверяемая гипотеза не верна
г) правило, устанавливающее условия, при которых проверяемую гипотезу следует отвергнуть
Тест 3.7. Нулевую гипотезу отвергают, если:
а) наблюдаемые значения статистики критерия попадают в критическую область
б) наблюдаемые значения статистики критерия не попадают в критическую область
в) наблюдаемые значения статистики критерия попадают в допустимую область
г) наблюдаемые значения статистики критерия равны нулю
Тест 3.8. Если нулевую гипотезу в результате проверки критерия отвергают, какова вероятность при этом совершить ошибку?
а) α б) β в) 1-β г) γ
Тест 3.9. Что называют ошибкой первого рода?
а) Гипотеза H0 верна и ее принимают согласно критерию
б) Гипотеза H0 верна, но ее отвергают согласно критерию
в) Гипотеза H0 неверна и ее отвергают согласно критерию
г) Гипотеза H0 неверна, но ее принимают согласно критерию
Тест 3.10. Что называют ошибкой второго рода?
а) Гипотеза H0 верна и ее принимают согласно критерию
б) Гипотеза H0 верна, но ее отвергают согласно критерию
в) Гипотеза H0 неверна и ее отвергают согласно критерию
г) Гипотеза H0 неверна, но ее принимают согласно критерию
Тест 3.11. Что называют мощностью критерия:
а) вероятность не допустить ошибку второго рода
б) вероятность не допустить ошибку первого рода
в) вероятность не допустить ошибку первого или второго рода
г) нет правильного ответа
Тест 3.12. Что называют мощностью критерия:
а) Гипотеза H0 верна и ее принимают согласно критерию
б) Гипотеза H0 верна, но ее отвергают согласно критерию
в) Гипотеза H0 неверна и ее отвергают согласно критерию
г) Гипотеза H0 неверна, но ее принимают согласно критерию
Тест 3.13. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать правостороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.14. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать левостороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.15. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать двустороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.16. Когда при проверке гипотезы H0: σ2=σ02 при H1: σ2=σ12 следует выбирать двустороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.17. Когда при проверке гипотезы H0: σ2=σ02 при H1: σ2=σ12 следует выбирать левостороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.18. Когда при проверке H0: σ2=σ02 при H1: σ2=σ12 следует выбирать правостороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.19. Какая статистика используется при проверке гипотезы о значении генеральной дисперсии H0: σ2=σ02:
а) 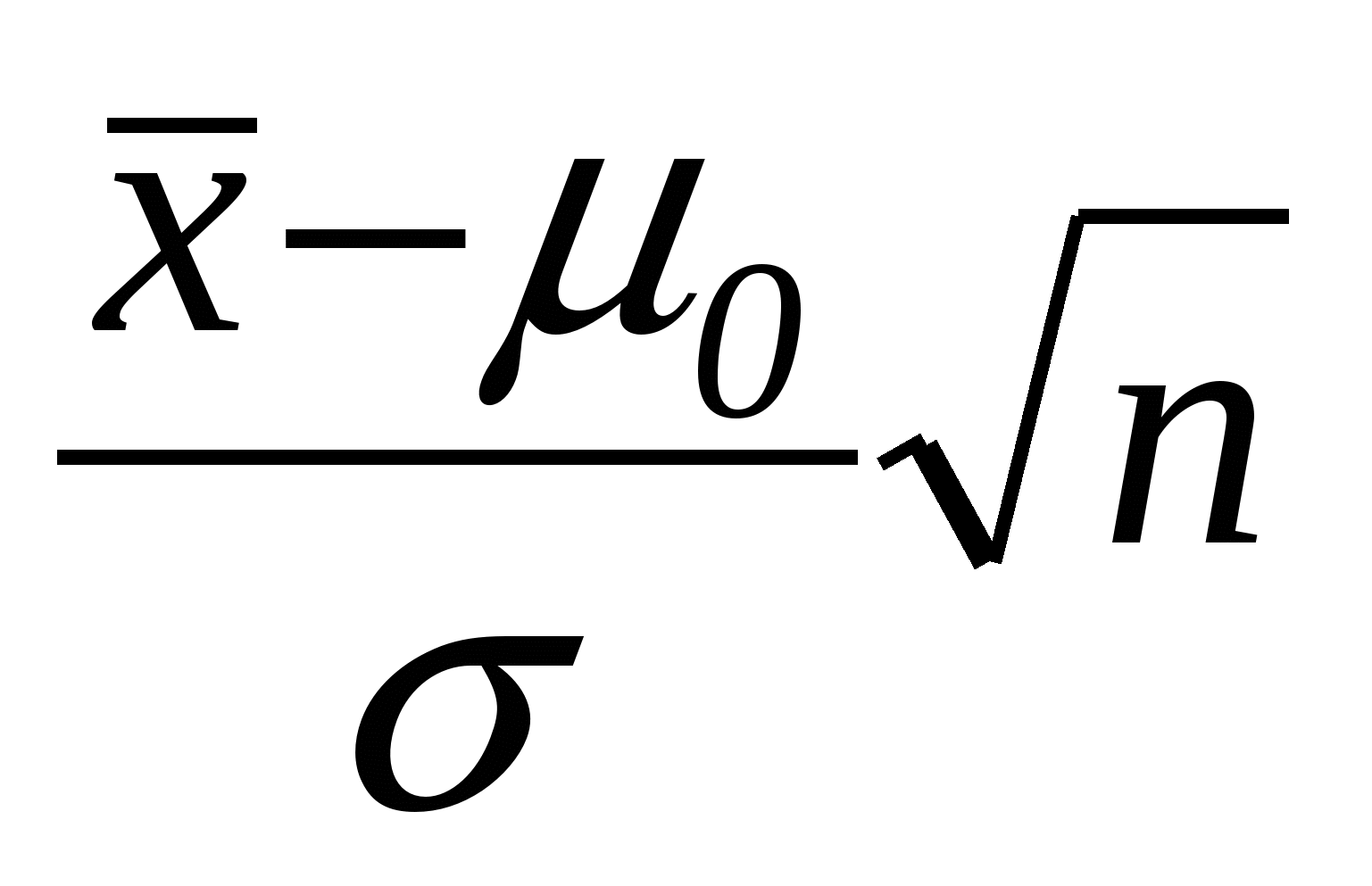 б) б) 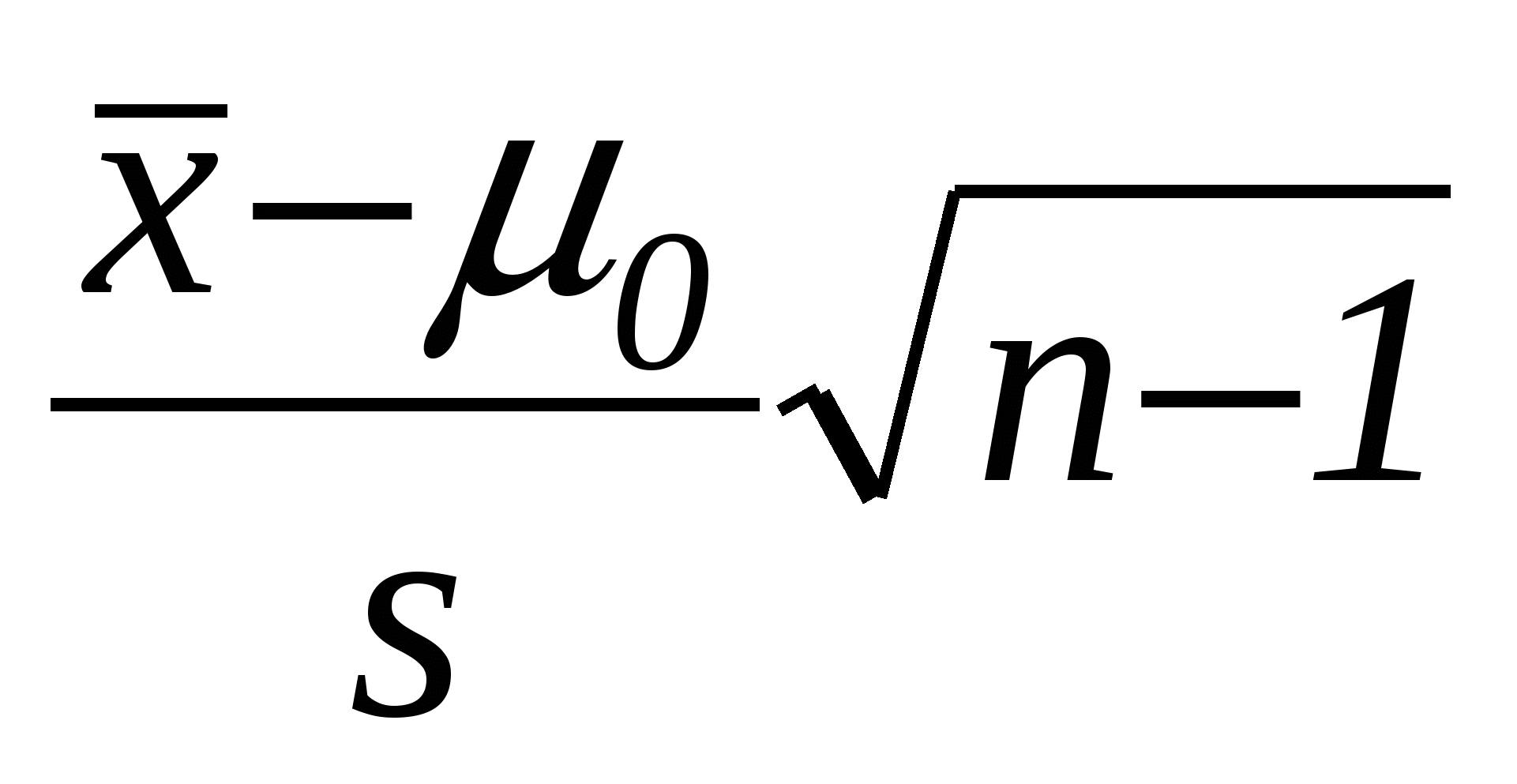 в) в) 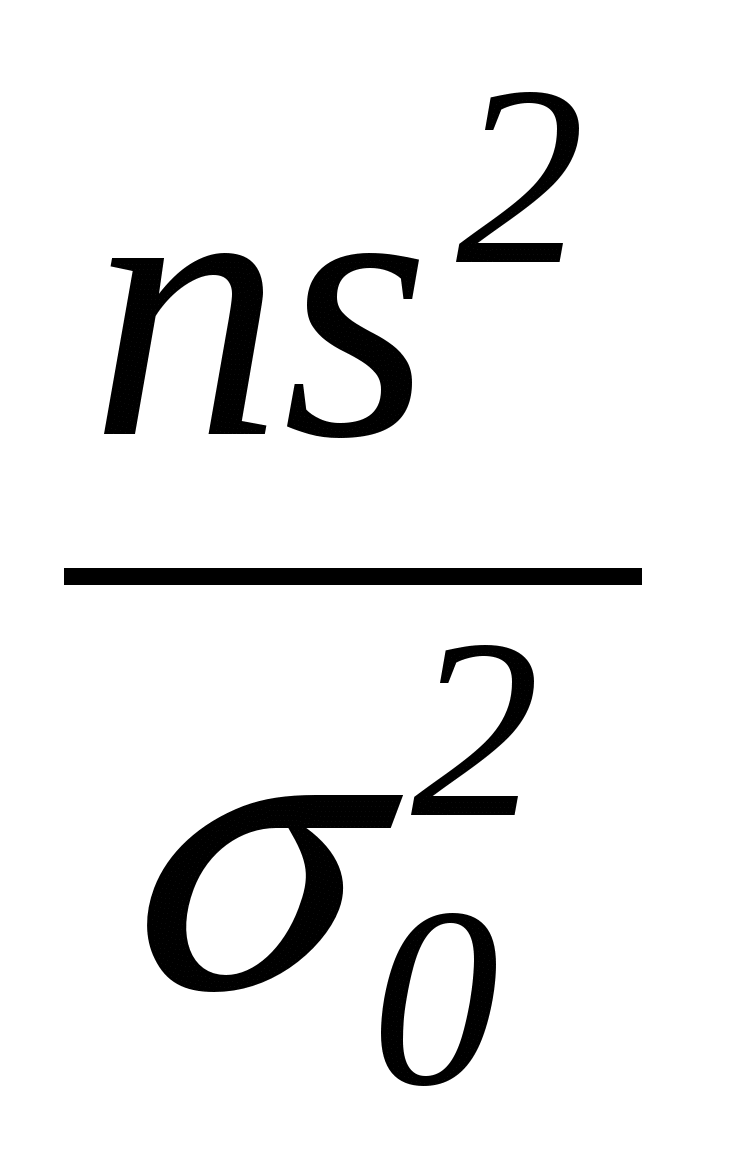 г) г) 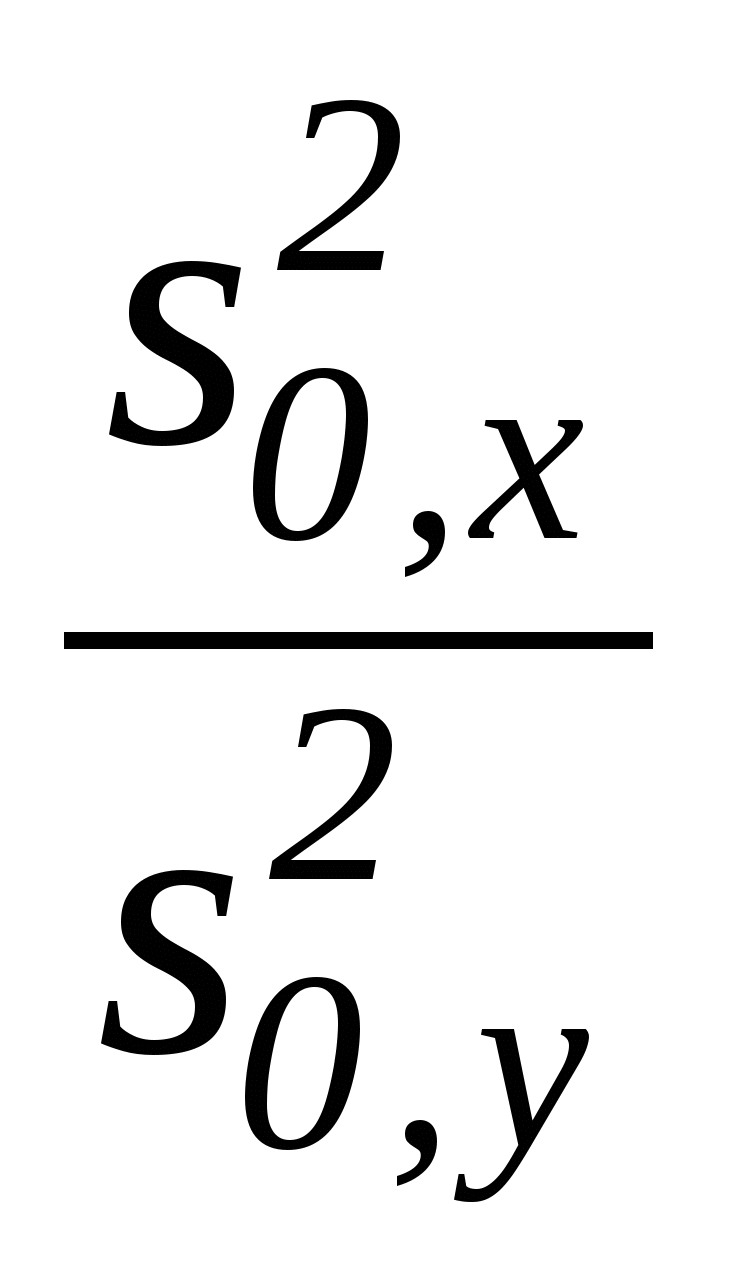
Тест 3.20. Какая статистика используется при проверке гипотезы о значении генеральной средней
H0: µ=µ0 при известной генеральной дисперсии:
а) 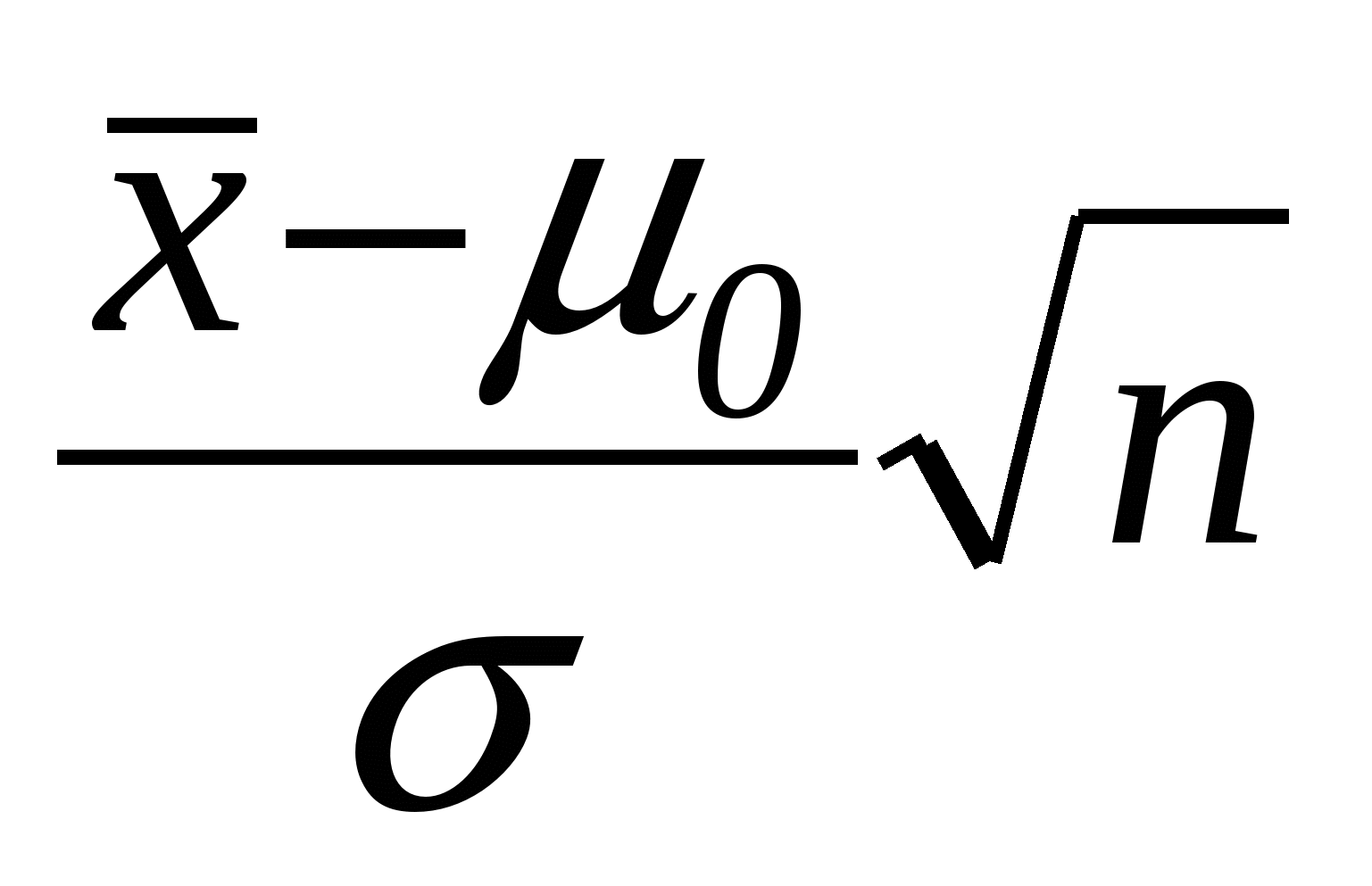 б) б) 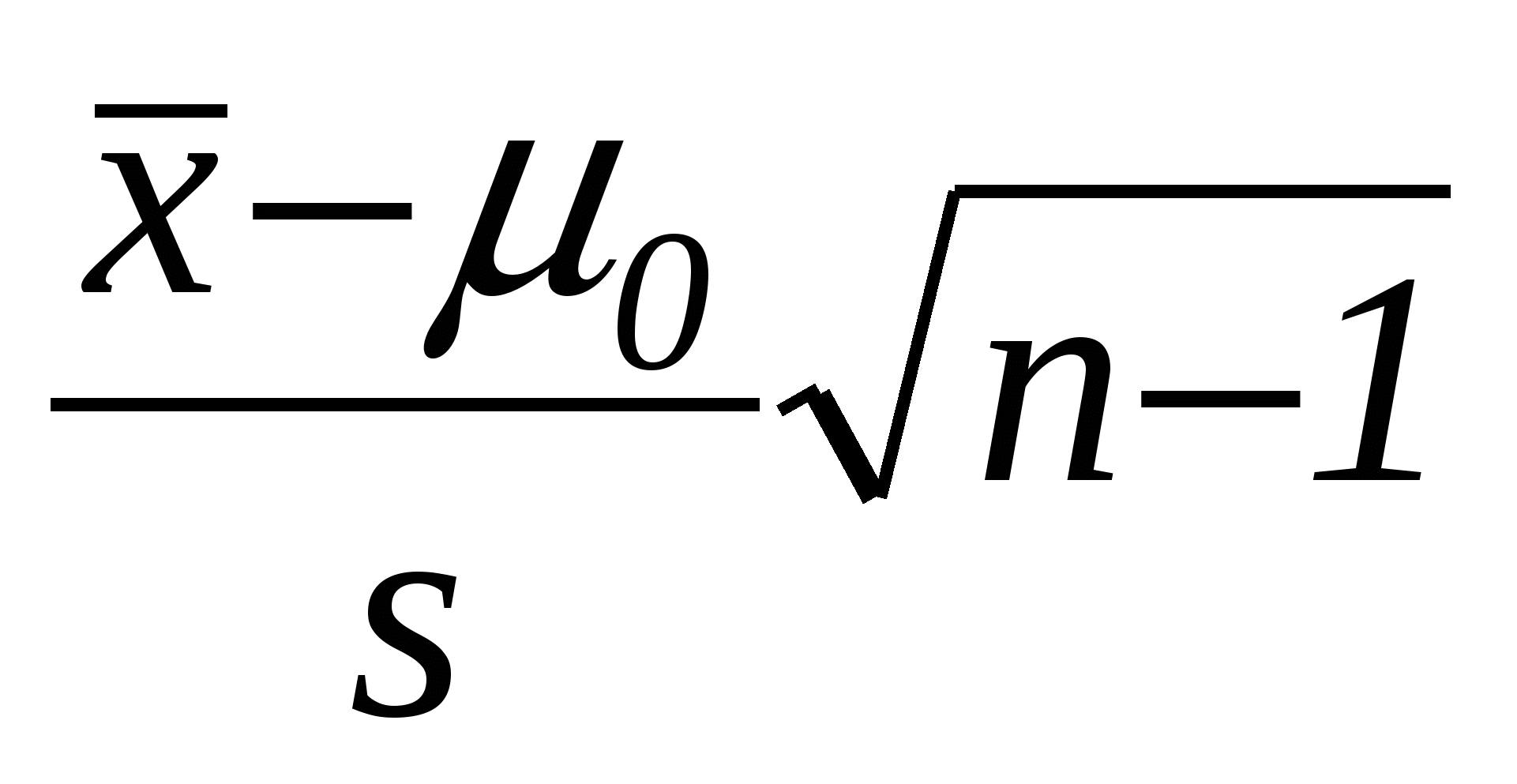 в) в) 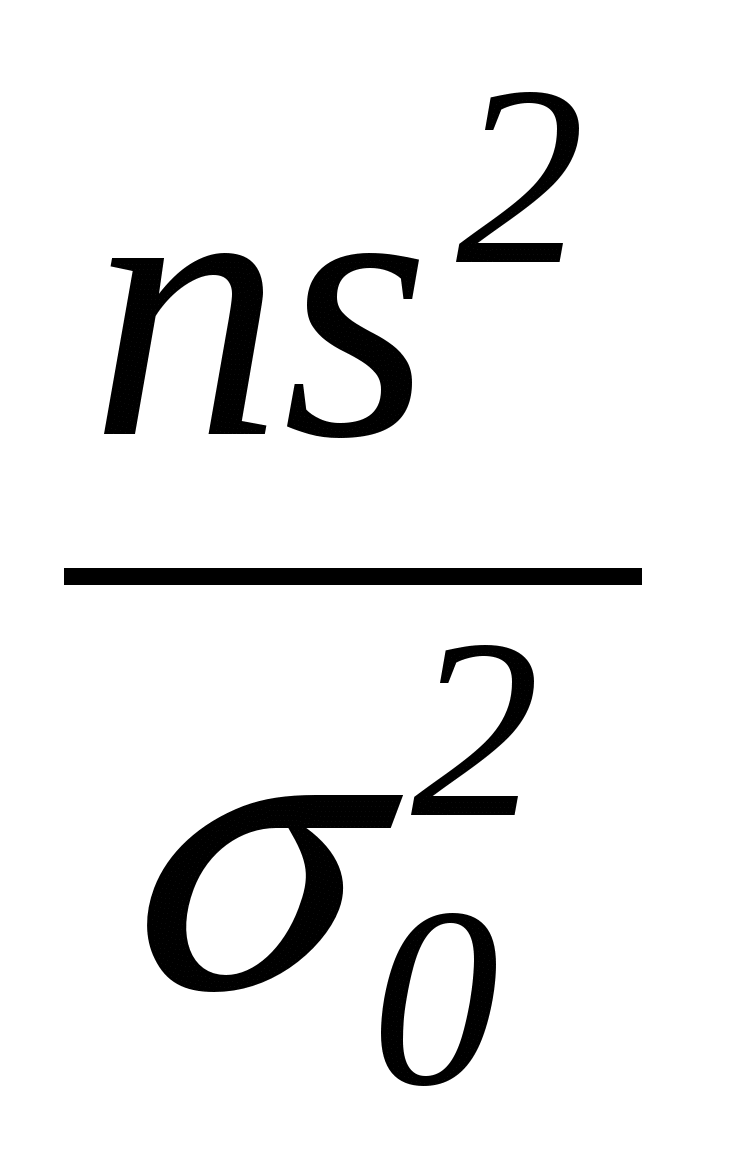 г) г) 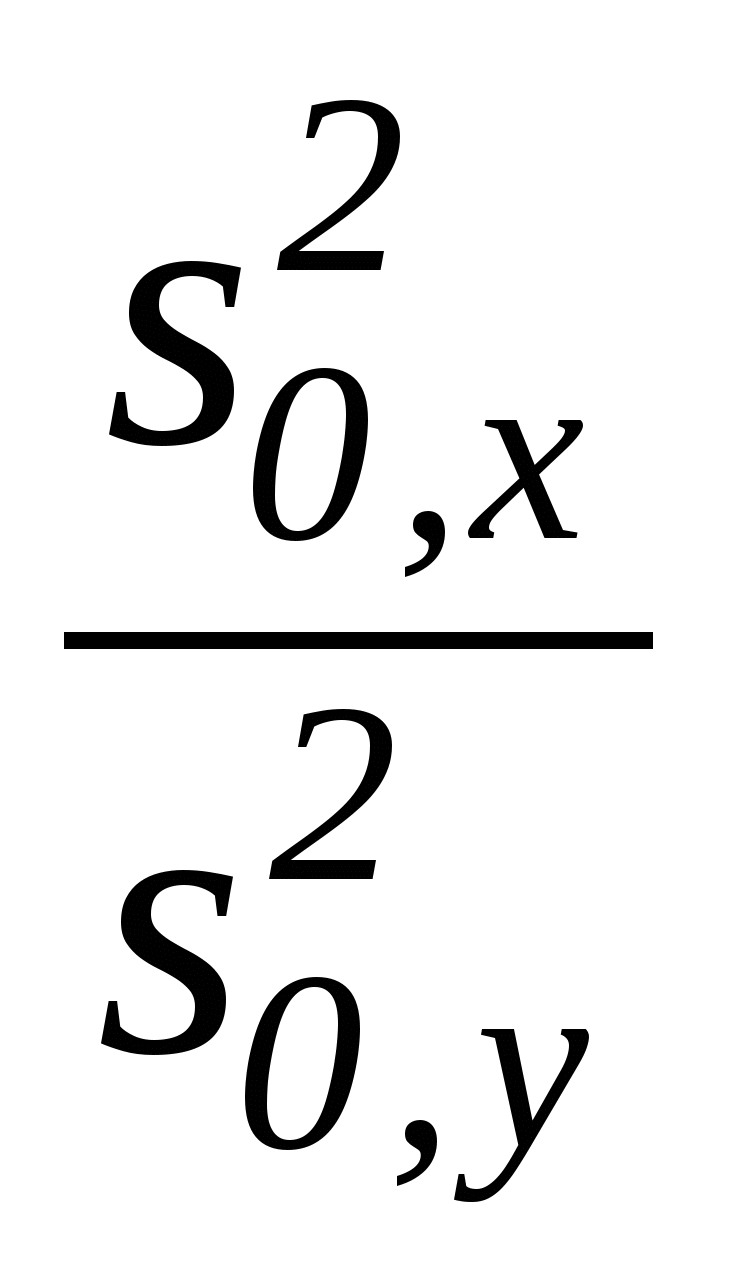
Тест 3.21. Какая статистика используется при проверке гипотезы о значении генеральной средней
H0: µ=µ0 при неизвестной генеральной дисперсии:
а) 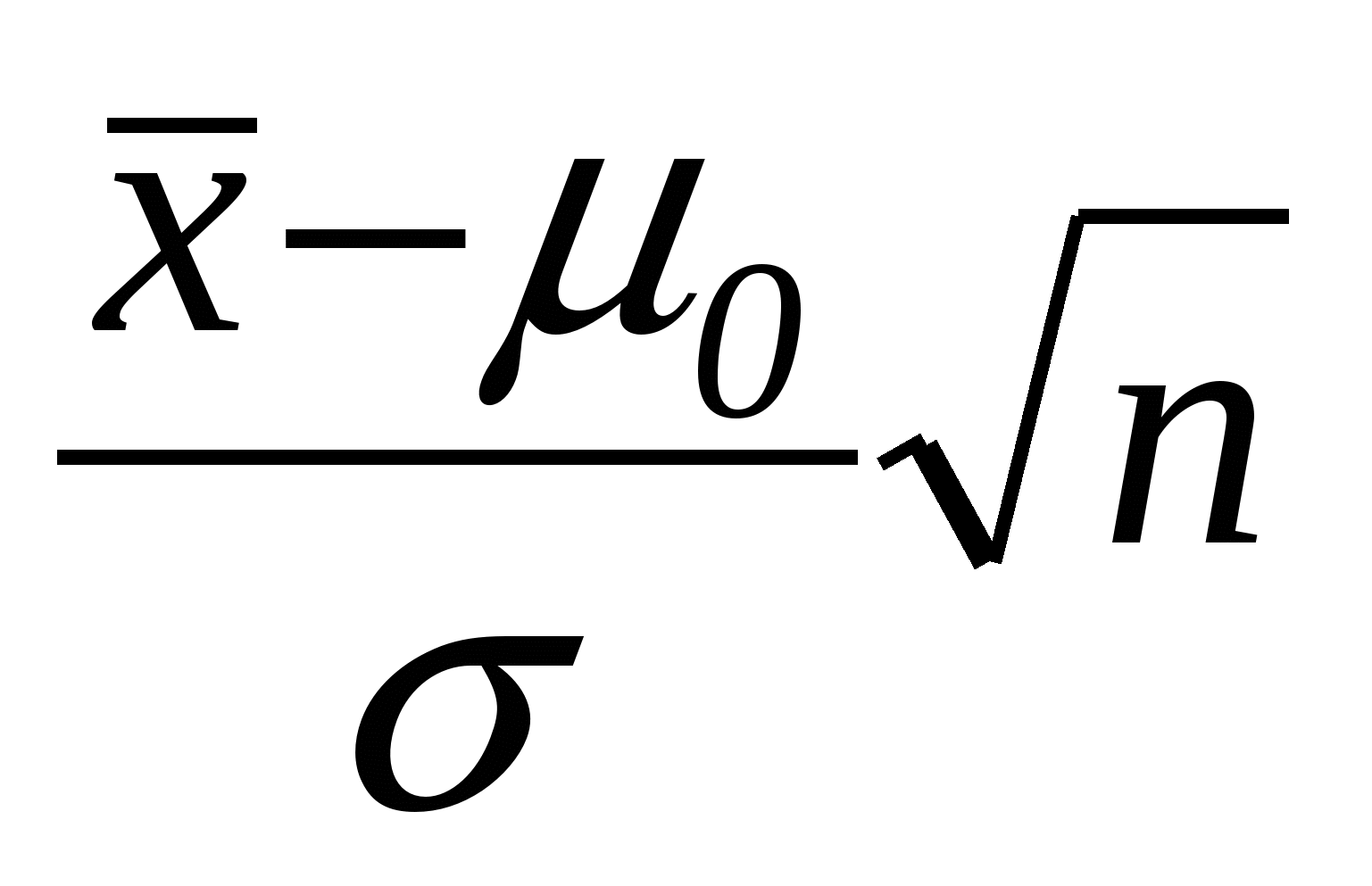 б) б) 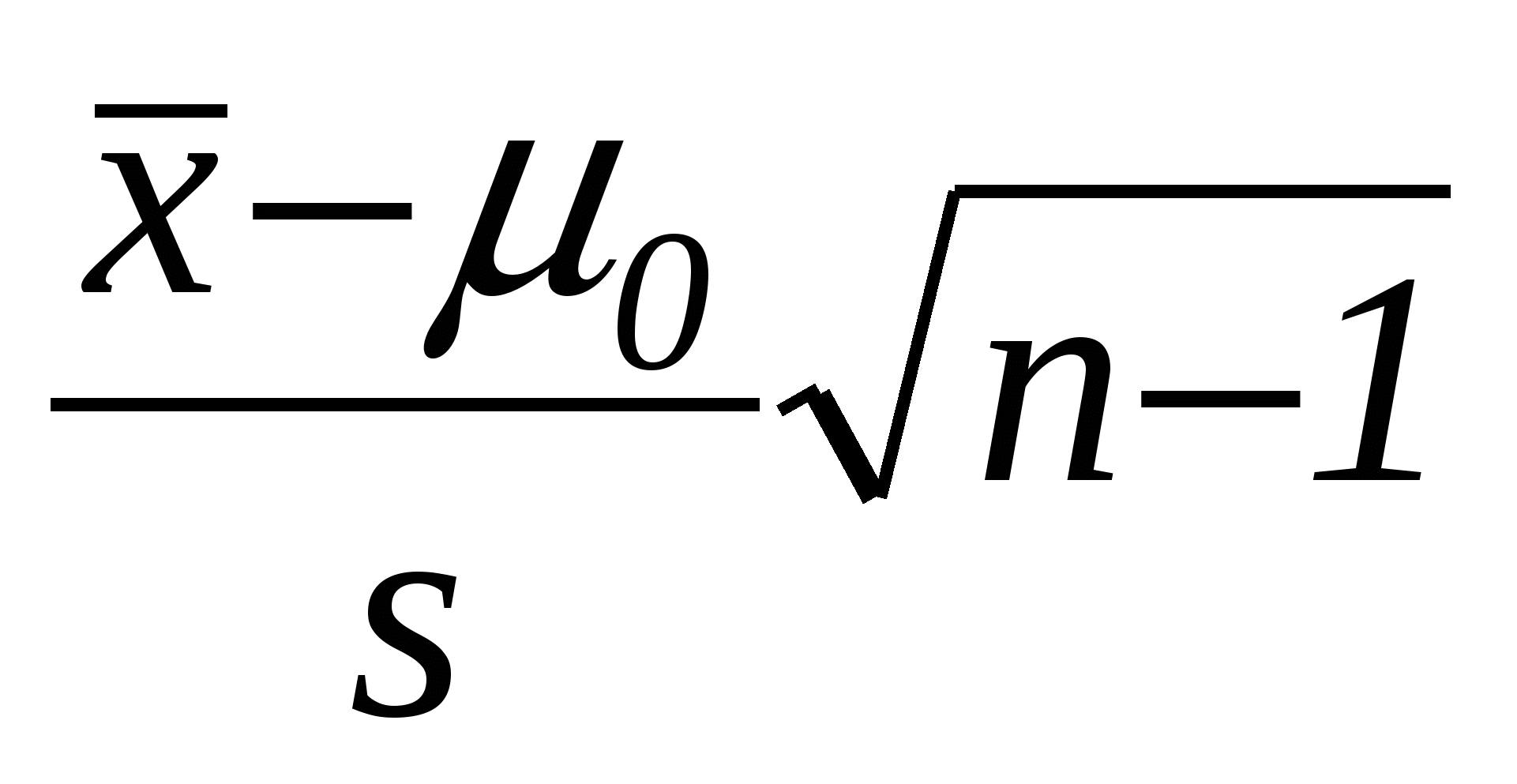 в) в) 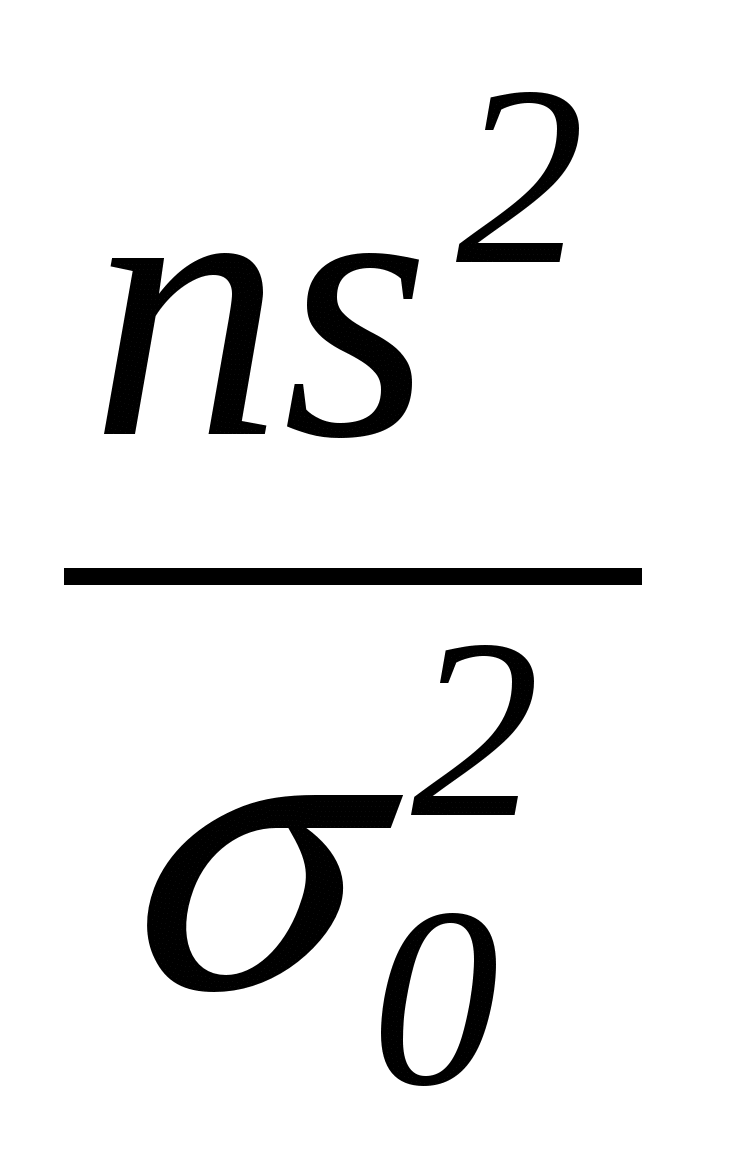 г) г) 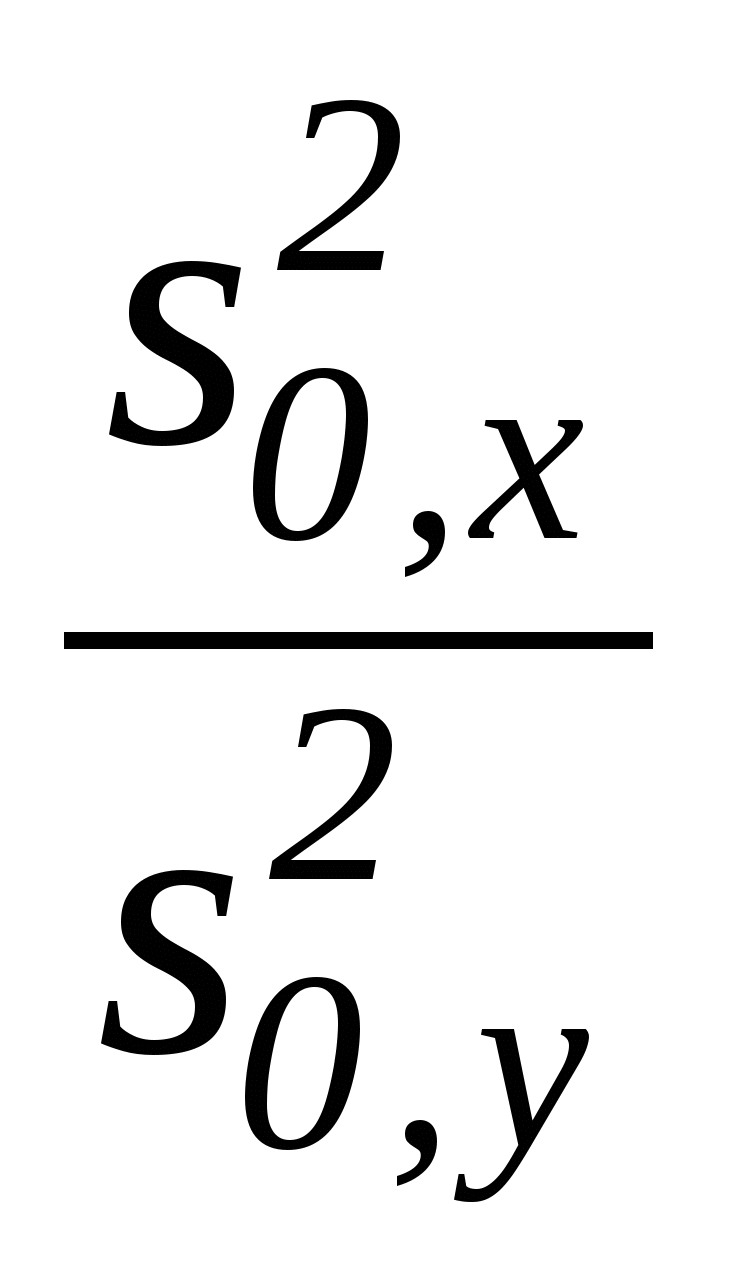
Тест 3.22. В каком критерии используется распределение Стьюдента?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
Тест 3.23. В каком критерии используется распределение Фишера-Снедекора?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.24. В каком критерии используется нормальное распределение?
а) при проверке гипотезы о равенстве вероятностей
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.25. В каком критерии используется распределение Пирсона?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
Тест 3.26. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать правостороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.27. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать левостороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.28. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать двустороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.29. Какая критическая область используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей H0: σx2=σy2 при H1: σx2≠σy2?
а) двусторонняя
б) левосторонняя
в) правосторонняя
Тест 3.30. Какая статистика используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей H0: σx2=σy2
а) 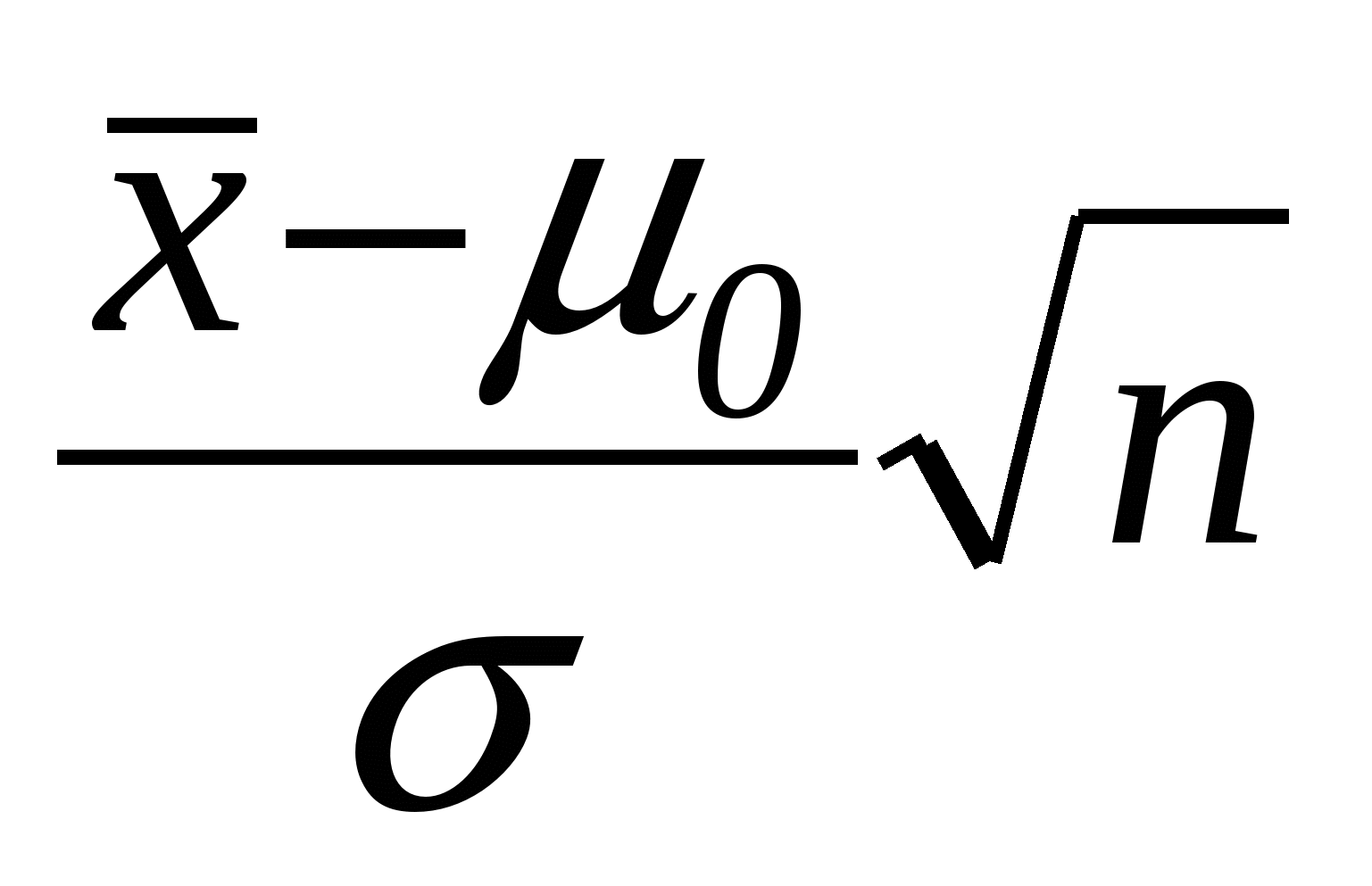 б) б) 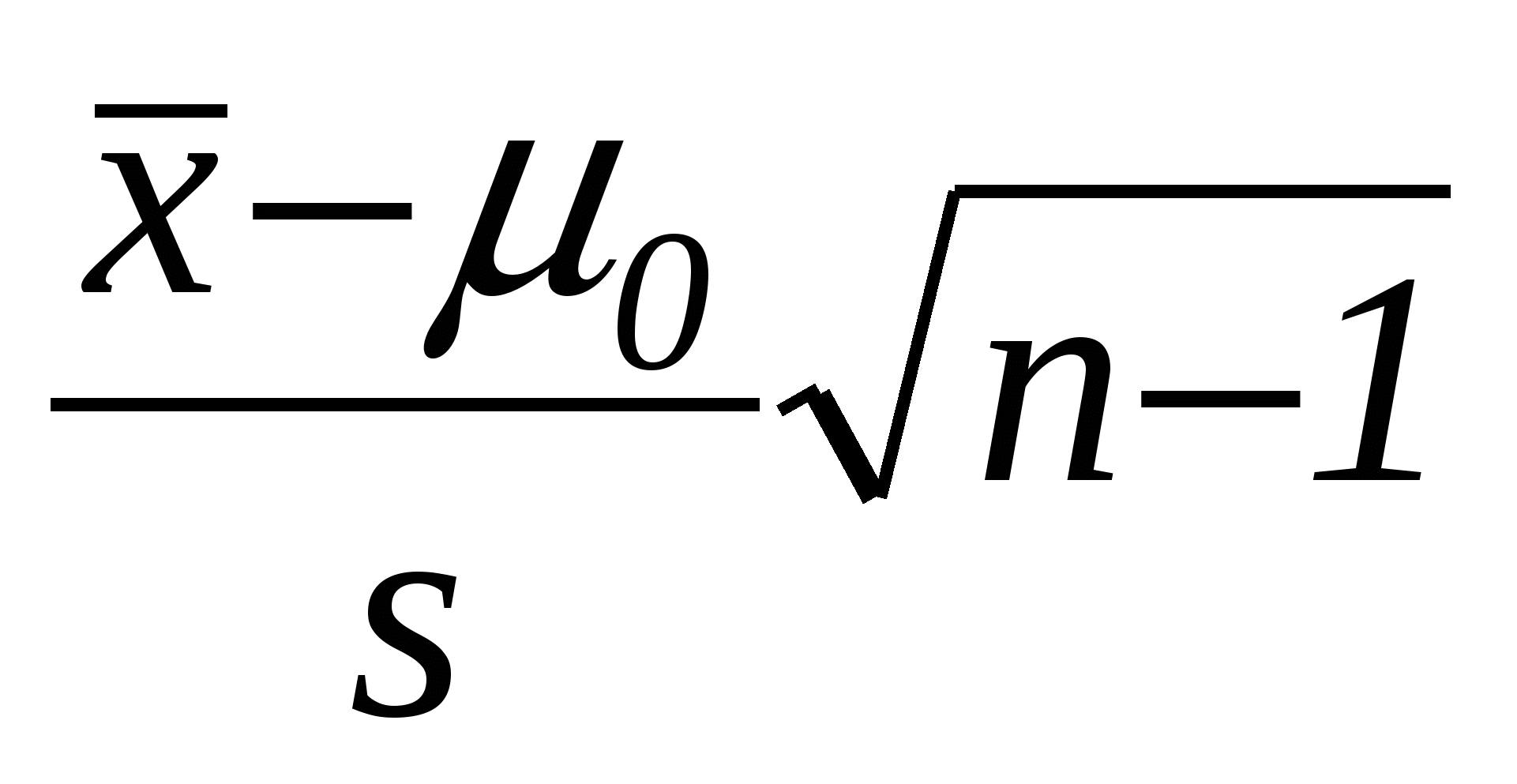 в) в) 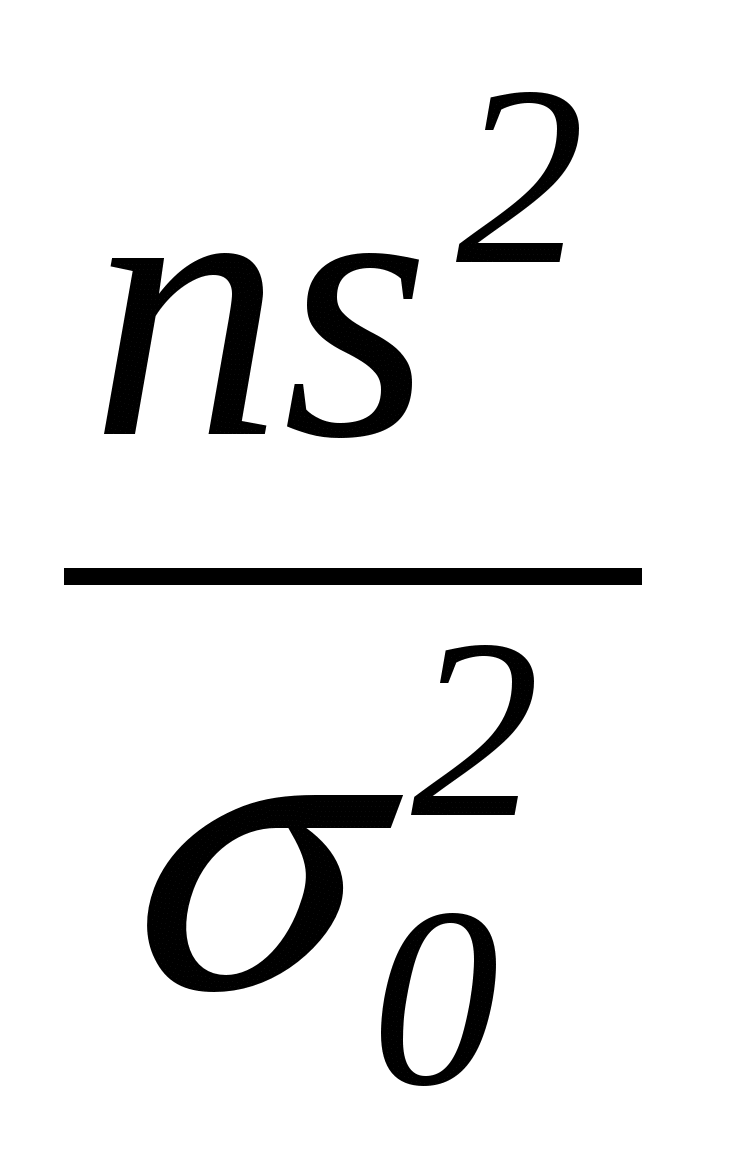 г) г) 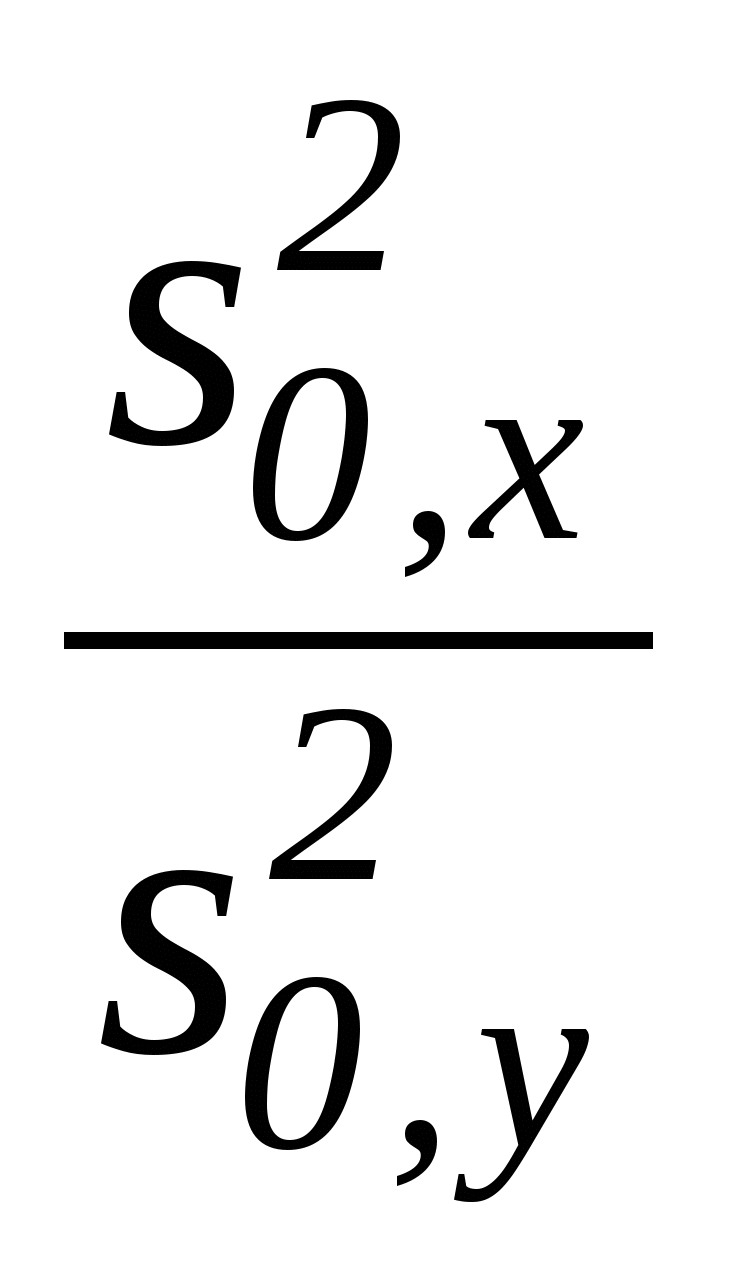
Тест 3.31. Для проверки какой гипотезы используется статистика 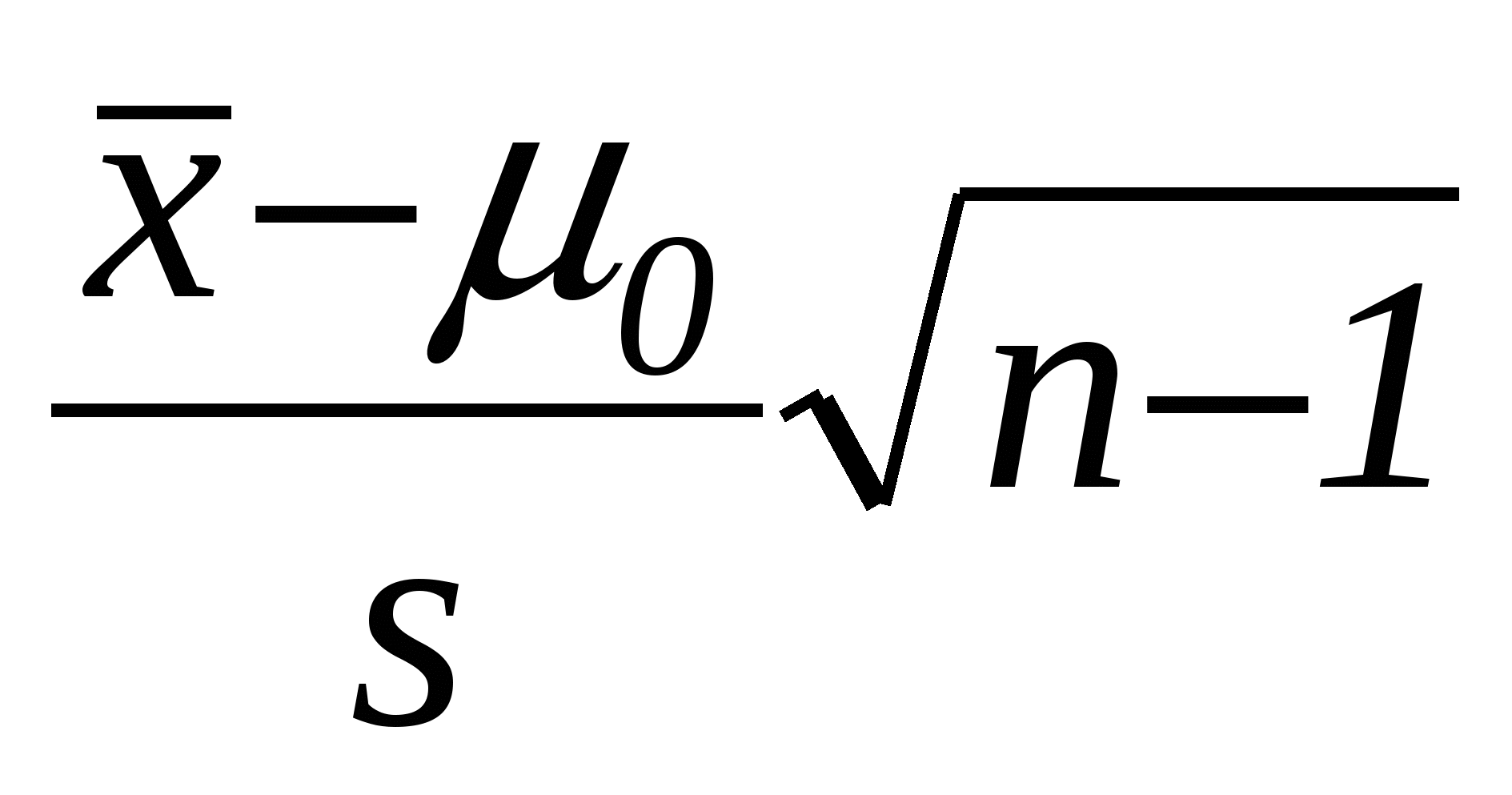
а) H0: р1=р2 б) H0: µ1=µ2 в) H0: σ12=σ22 г) нет правильного ответа
Тест 3.32. При проверке гипотезы о значении генеральной средней гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.33. При проверке гипотезы о значении вероятности события гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.34. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей гипотеза H0 не отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.35. При проверке гипотезы о значении генеральной средней при неизвестной генеральной дисперсии используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.36. При проверке гипотезы о значении генеральной средней при известной дисперсии используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.37. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с неизвестными генеральными дисперсиями используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.38. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с известными генеральными дисперсиями используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.46. По какому принципу выбирается критическая область?
а) вероятность попадания в нее должна быть минимальной, если верна гипотеза H0 и максимальной в противном случае
б) вероятность попадания в нее должна быть минимальной, если верна гипотеза H1 и максимальной в противном случае
в) вероятность попадания в нее должна быть равна 0
г) вероятность попадания в нее должна быть максимальной, если верна гипотеза H0 и минимальной в противном случае
Тест 3.47. Границы правосторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(Sкр)=α
в) P(S>Sкр.пр)=α/2; P(Sкр.лев)=α/2
г) нет правильного ответа
Тест 3.48. Границы левосторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(Sкр)=α
в) P(S>Sкр.пр)=α/2; P(Sкр.лев)=α/2
г) нет правильного ответа
Тест 3.49. Границы двусторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(Sкр)=α
в) P(S>Sкр.пр)=α/2; P(Sкр.лев)=α/2
г) нет правильного ответа |
 Скачать 168.5 Kb.
Скачать 168.5 Kb.