цуыв. Тестовые задания по разделам изучения содержания дисциплины

• Название: Тестовые задания по разделам изучения содержания дисциплины
• Дата: 21.12.2022
• Размер: 250.83 Kb.
• Имя файла: Matematicheskoe_modelirovanie_sistem_i_protsessov_A_V_5_sem_ekza.docx
• Тип: Документы; #857844
• страница: 28 из 28

ВВОД

Решение …. дифференциального уравнения в частных производных с постоянными коэффициентами, отражающее устойчивость бесстыкового пути,

может быть найдено методом Фурье, как произведение двух функций

y_ x, _  U_ x_ f__

В1 + однородного

ВВОД

Функция U(x), определяющая положение продольных сил в бесстыковом пути в …

^{пространстве имеет следующий вид EIUIV} ^x ^{ FUII} ^x ^{ QU} ^x ^{ 0}

В1 + двухмерном

ВВОД

Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие …, имеет вид

^{ } 2x

^ 4EI^ F

4^{2 }2 ^

y_ x, _  Аch_

^x_^{cos exp} _{ 2 }

 



^
  <sup>l

</sup>  _ 4EI l _ ^

 

В1 + поездов

ВВОД

Решение дифференциального уравнения изменений … перемещений под дей- ствием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие поездов для точки х=0имеет вид

^ 4EI^ F ^{2 }2 ^




^
y_0, _  f₀ exp^ _{ 2 }



^  _ 4EI l _ ^

 

В1 + поперечных

ВВОД

Решение дифференциального уравнения изменений поперечных перемещений под действием продольных растягивающих сил в бесстыковом пути для …, учитывающей воздействие поездов, имеет вид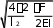

^{ } 2x

^ 2, 25F² ^

y_ x, _  Ach_{ }cos _l

exp_ 

EI ^

_{ }  

В1 + модели

ВВОД

Решение дифференциального уравнения изменений поперечных перемещений под действием … продольных сил в бесстыковом пути для модели, учитывающей

^ 2, 25F² ^

воздействие поездов в точке х=0имеет вид

^y^{0, } ^

f₀ exp_ 

EI ^

 

В1 + растягивающих

ВВОД


Дифференциальное уравнение изменений поперечных перемещений под дей- ствием продольных … сил в бесстыковом пути для модели, учитывающей воздействие поездов для кривого участка будет иметь следующий вид

⁴ yEI_x4

² y^Fx²

_{ } y_ F

 R

В1 + сжимающих

ВВОД

2 ^
Решение дифференциального уравнения изменений … перемещений под дей- ствием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие поездов, имеет вид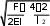

^{ } x

^ 4EI^ F

4^{2 }2 ^

l^{2 }

4x^{2 }

^y ^{x, } ^{ Ach}_

x_cos exp^ _



^ 

^1 2 ^


  <sup>l

</sup>  _ 4EI l _

^ 8R_ l _

 

В1 + поперечных

ВВОД

Решение дифференциального уравнения изменений поперечных перемещений под действием продольных … сил в бесстыковом пути для модели, учитывающей воздействие поездов для точки х=0имеет вид

^ 4EI^ F 4^{2 }2 ^ l²



₂ 
y_0, _ 

f₀ exp^ _ ^ 

 

^  _ 4EI l _ ^ 8R

 

В1 + сжимающих

ВВОД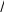

Решение дифференциального уравнения изменений … перемещений под дей- ствием продольных сжимающих сил в бесстыковом пути для модели,

учитывающей воздействие поездов для точки х=0при

l²  4²EIF

имеет вид

^ 6, 25F² ^ ²EI

^y^{0, } ^

f₀ exp_

EI

^{ } 2RF

 

В1 + поперечных

ВВОД

Опасная …. роста стрелы изгиба рельсов в плане определяется по формуле

• 
  6, 25 fF² 6, 25F²
  

y_0, _ ⁰ exp

EI

В1 + скорость


EI