Контрольная работа предмет Математические основы цифровой обработки сигналов.. Контрольная работа. Тические основы цифровой обработки сигналов
 Скачать 4.74 Mb. Скачать 4.74 Mb.
|
|
Министерство Российской Федерации по Связи и Информатизации Сибирский Государственный Университет Телекоммуникаций и Информатики, Кафедра РТС Контрольная работа предмет: Математические основы цифровой обработки сигналов. Выполнил: студент группы ЗС-91 Лубкин В.В. Проверил: __________________ Новосибирск-2012г Содержание
Непрерывное сообщение передается по системе связи дискретными сигналами. На стороне передачи исходное сообщение преобразуется в первичный электрический сигнал, который, в свою очередь, преобразуется в цифровую форму. Перед передачей в канал связи сообщения производится также предварительная обработка его цифрового представления по заданному алгоритму. На стороне приема восстанавливается непрерывное сообщение (с учетом предварительной обработки на стороне передачи), которое и выдается получателю. Значения сигнала сообщения изменяются в пределах от 0 до Umax = 10 В. Сигнал сообщения перед преобразованием в цифровую форму пропускается через фильтр нижних частот с частотой среза Fв = 10 кГц. Интервал между отсчетами берется в k = 4 раза меньшим по сравнению с шагом дискретизации, определяемым теоремой Котельникова. Отсчеты после дискретизации представляются 10-разрядными двоичными числами. Последние поступают на цифровой фильтра, осуществляющий предварительную обработку с соответствии с алгоритмом вида yk = 4xk + 3,5xk–1 – 2 xk–2. Задача №1 Непрерывное сообщение передается от источника к получателю по дискретному каналу связи. Требуется: 1. Изобразить обобщенную структурную схему системы связи для передачи непрерывных сообщений дискретными сигналами, привести подробное описание назначения входящих в нее блоков. Преобразование сообщения и сигналов в системе связи проиллюстрировать (качественно) приведением временных и спектральных диаграмм для следующих точек тракта: на выходе источника непрерывного сообщения (сигнала); на входе преобразователя «аналог-цифра» (на выходе ФНЧ); дискретизированной последовательности (АИМ-сигнала, с учетом заданных значений Umax, Fв и k); на выходе АЦП (последовательность чисел, соответствующих отсчетам входного сигнала – для заданных Umax и n); Описать временные и спектральные диаграммы. 2. Найти величину шага квантования Uкв и дисперсия шума Исходные данные: Umax= 10 В; Fв = 10 кГц; k = 4; n= 10. Решение. Обобщенная структурная схема системы связи приведена на рисунке 1.1. 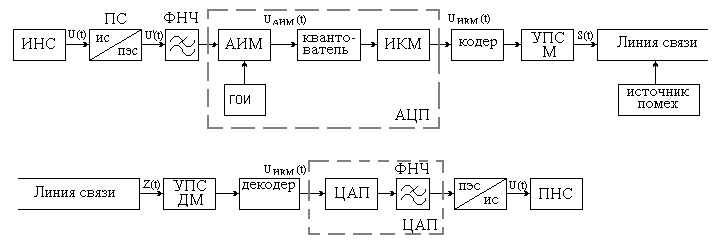 Рисунок 1.1 – Обобщенная структурная схема системы передачи непрерывных сообщений дискретных сигналов Рисунок 1.1 – Обобщенная структурная схема системы передачи непрерывных сообщений дискретных сигналовСообщение от источника непрерывных сообщений (ИНС) поступает на преобразователь сигнала (ПС), который преобразует исходное сообщение (ИС) в первичный электрический сигнал (ПЭС) U’(t). Спектр электрического сигнала U(t) перед дискретизацией подвергается ограничению до частоты Fв фильтром нижних частот (ФНЧ). Далее сигнал поступает на аналого-цифровой преобразователь (АЦП) для преобразования непрерывного сигнала в цифровой сигнал. Аналого-цифровое преобразование производится в три этапа: Этап 1: непрерывный сигнал представляется дискретными отсчетами U(kt) через равные временные интервалы равные t, с помощью амплитудно-импульсного модулятора (АИМ). Для получения АИМ-сигнала на входе модулятора подаются отсчетные импульсы t от генератора отсчетных импульсов (ГОИ). Этап 2: полученные дискретные отсчеты U(kt)=UАИМ(t) подвергаются квантованию по уровню. Вместо данного значения передаваемого сигнала UАИМ(t) передаются ближайшие значения квантованных уровней, то есть приближенно округленных значений UК. Этап 3: полученные квантованные значения представляются в виде последовательности n-значных кодовых комбинаций, по средством импульсно-кодовой модуляции (ИКМ). На практике уровни квантования представляются в двоичной системе счисления. После аналого-цифрового преобразования цифровой сигнал поступает на кодер, в котором последовательность кодовых символов дополнительно преобразуется, т.е. в код вводится избыточность для улучшения помехоустойчивости. Далее сигнал поступает на устройство преобразования сигнала (УПС) т.е. в модулятор (М), в котором передаваемая последовательность двоичных импульсов преобразуется в радиоимпульсы. Из УПС сигнал поступает в линию связи, где по прохождению сигнал ослабляется и на него накладываются помехи от источников помех. На приемном конце в УПС демодуляторе (Д), происходит регенерация сигнала и обратные преобразования из радиоимпульсов в последовательность двоичных импульсов. Из принятого сигнала в декодере восстанавливается m-значная кодовая последовательность, равная квантованным уровням. Полученная кодовая последовательность подвергается цифро-аналоговому преобразованию (ЦАП), т.е. восстанавливается непрерывное сообщение в соответствии с принятыми последовательностями кодовых комбинаций. Цифро-аналоговому преобразование производится в два этапа: Этап 1: кодовые комбинации преобразуются в квантованную последовательность отсчетов. Этап 2: сглаживающий ФНЧ восстанавливает непрерывный сигнал. Далее восстановленный первичный электрический сигнал преобразуется в исходное сообщение, которое доставляется получателю непрерывного сообщения (ПНС). Временные и спектральные диаграммы для точек указанных в задании приведены на рисунках 1.2, 1.3 и 1.4.
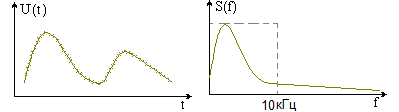
Рисунок 1.2 – Диаграмма сигнала на выходе источника непрерывного сообщения Исходный сигнал U(t) имеет произвольную форму и бесконечный спектр. Необходимо в соответствии с теоремой Котельникова ограничить спектр исходного сигнала частотой Fв = 10 кГц.
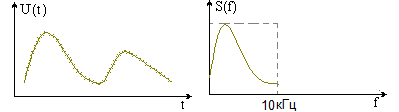
Рисунок 1.3 – Диаграмма сигнала на выходе ФНЧ Ф  НЧ сглаживает исходный сигнал и ограничивает спектр исходного сигнала, это ограничение вносит минимальные потери сигнала, т.к. в полученном спектре сосредоточено 90-95% мощности исходного сигнала.
Рисунок 1.4 – Диаграмма сигнала на выходе АИМ На вход АИМ поступают отсчетные импульсы с интервалом Спектральная диаграмма АИМ сигнала содержит ограниченный спектр исходного сигнала и спектры прямоугольных импульсов, поступающих с генератора отсчетных импульсов (ГОИ) на дискретизатор (верхние и нижние боковые полосы на частотах fД и 2fД). Частоты на спектральной диаграмме на выходе АИМ: Временная диаграмма АИМ сигнала представляет собой последовательность отсчетов взятых через интервал времени Каждый отсчет представляется n-значным кодом в двоичной системе счисления. Произведем импульсно-кодовую модуляцию над отсчетом равным Umax. Для этого необходимо рассчитать шаг квантования. Шаг квантования: Дисперсия шага квантования: Для того, чтобы закодировать уровень 9 В с шагом квантования 0,0088 В потребуется 10-разрядный двоичный код. Кодируем 1023-ий уровень квантования, так как N = 2n – 1 = 210 – 1 = 1023. UК = U1023= 1111111111. На рисунке 1.5 изображена временная диаграмма для 1023-го квантованного отсчета. Спектр S(t) имеет в общем случае сложную форму. 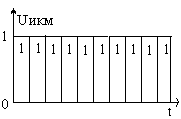 Рисунок 1.5 – Временная диаграмма для 1023-го квантованного отсчета Задача №2 В предположении, что сигнал сообщения имеет гармоническую форму с частотой Fв = 10 кГц и амплитудой Umax = 10 В, требуется: 1. Изобразить временные диаграммы исходного сигнала (2, 3 периода) и дискретизированной последовательности для него при условии, что дискретизация отсчетами производится с интервалом в k = 4 раза меньшим по сравнению с шагом дискретизации, определяемым теоремой Котельникова. 2. Изобразить спектральные диаграммы исходного сигнала и дискретизированной последовательности. 3. Описать (с обоснованием) вид графиков временных и спектральных диаграмм на основе соответствующих теоретических положений. Исходные данные: Umax= 10 В; Fв = 10 кГц; k= 4. Решение. Исходный гармонический сигнал имеет вид: Период Нули функции U(t) находятся из выражения Тогда 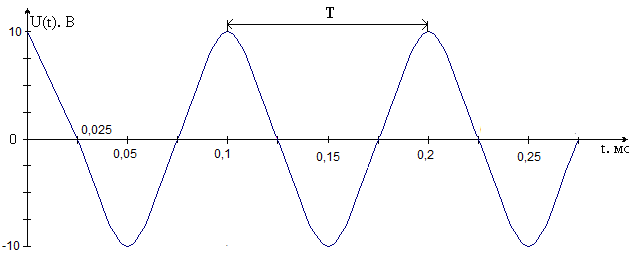 Рисунок 2.1 – Временная диаграмма исходного гармонического сигнала Для получения АИМ сигнала рассчитывается шаг дискретизации (эта величина уже была найдена в задаче 1): На выходе АИМ имеем дискретизированую последовательность с шагом дискретизации t=0,0125 мс. 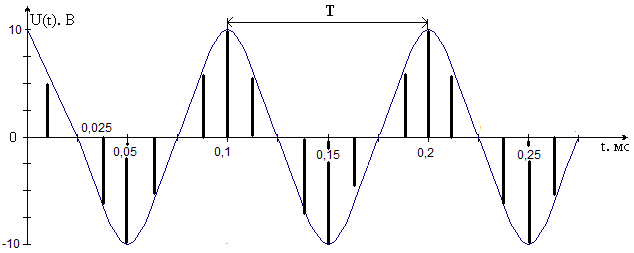 Рисунок 2.2 – Временная диаграмма дискретной последовательности с шагом дискретизацииt=0,0125 мс По свойству дискретного косинуса: Получаем: Спектр исходного сигнала имеет одну спектральную линию на частоте FВ = 10кГц с амплитудой равной UMAX = 10 В (рисунок 2.3). 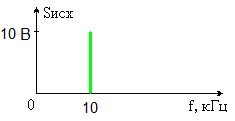 Рисунок 2.3 – Спектр исходного сигнала Спектр отсчетных импульсов, поступающих на вход АИМ расположен на частотах: Спектр дискретизированной последовательности будет содержать (рисунок 2.4): спектральную линию исходного сигнала; спектральную линию периодичности отсчетных импульсов на частотах fД, 2fД, 3fД и т.д. спектральные линии на частотах: 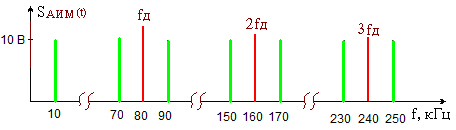 Рисунок 2.4 – Спектр дискретизированной последовательности Задача 3 1. В соответствии с дискретным преобразованием Фурье рассчитать и построить спектр заданного сигнала. Заданный сигнал представляет собой двоичную дискретную последовательность 11100. 2. Выполнить восстановление исходного сигнала по найденному в п.1 спектру, для чего: а) записать выражение для исходного сигнала в виде суммы гармонических составляющих (ряд Фурье); б) изобразить график восстановленного сигнала для интервала времени, равного длительности одной выборки. Решение. Прямое дискретное преобразование Фурье: k-порядковый номер отсчета времени выборки изменяется в пределах от 0 k N-1 (0 k 4); n- порядковый номер отсчета в частотной выборке; Хk- абсолютное значение (величина) k-го отсчета; Сn- абсолютное значение (величина амплитуды) n-го отсчета в частотной области. 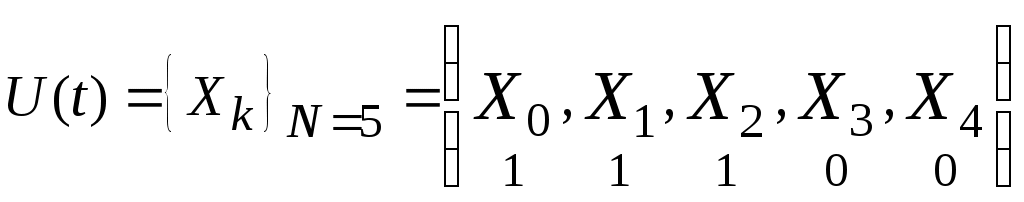 Получаем: постоянная составляющая для этой последовательности 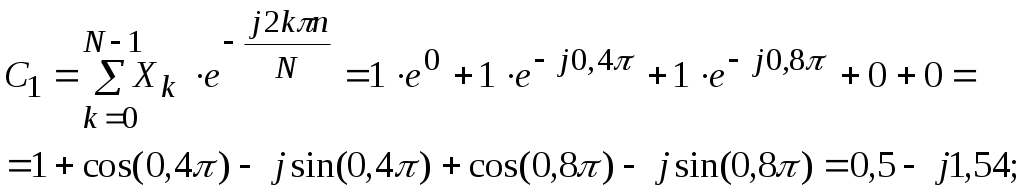 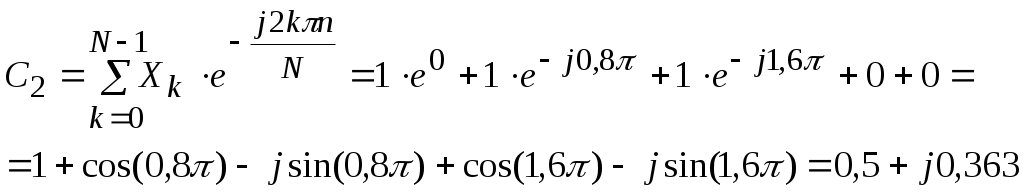 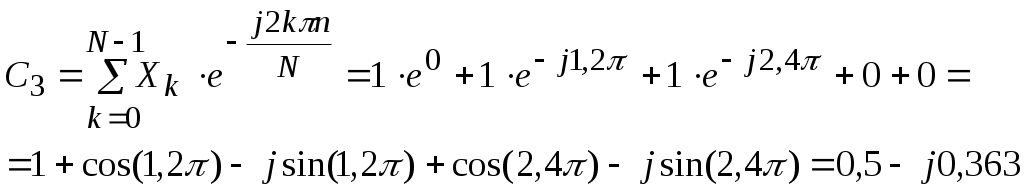 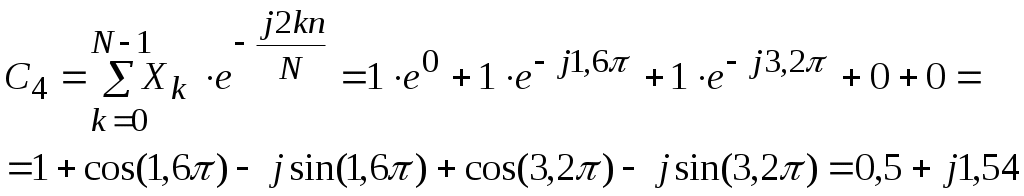 Найдем модули и фазы: Остальные отсчеты найдем как комплексно сопряженные по Гильберту, то есть различия в их фазах на угол 900 при одинаковых амплитудах. 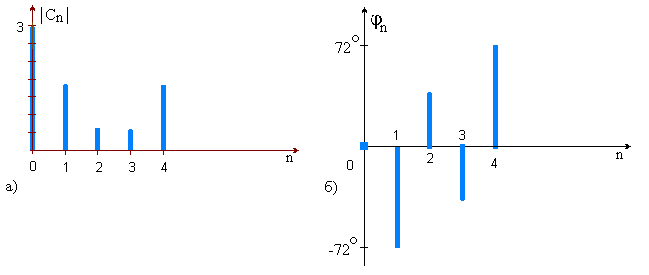 Рисунок 3.1 – Спектр амплитуд (а) и спектр фаз (б) Рисунок 3.1 – Спектр амплитуд (а) и спектр фаз (б)Восстановление исходного сигнала по найденному спектру. Исходный сигнал запишем в виде суммы гармонических колебаний: Подставим полученные значения Сnи n в формулу исходного сигнала, а результаты расчетов сведем в таблицу 3.1. Таблица 3.1
По полученным данным строим график зависимости U(t) от t/T. 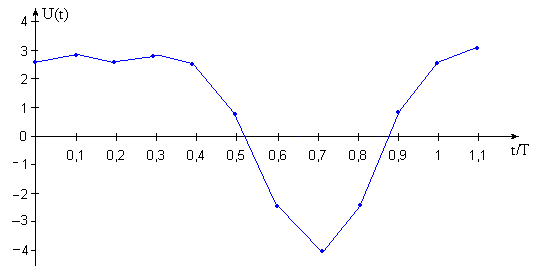 Рисунок 3.2 – График зависимости исходного сигнала от t/T. Задача 4 На стороне передачи осуществляется предварительная цифровая обработка сигнала, поступающего с выхода АЦП, в соответствии с алгоритмом вида yk =akxk + ak–1xk–1 + ak–2xk–2 = 4xk + 3,5xk–1 – 2xk–2. Требуется: 1. Изобразить структурную схему цифрового фильтра (ЦФ) и описать принцип его работы. 2. Определить импульсную характеристику данного ЦФ. 3. Определить системную функцию ЦФ. 4. Определить сигнал на выходе цифрового фильтра для отсчетов одного периода сигнала задачи 3. Построить временную диаграмму соответствующего ему аналогового эквивалента и сравнить с исходным. Исходные данные: Весовые коэффициенты: аk= а0 = 4; аk-1 = а1 = 3,5; аk-2 = а2 = –2; вид сигнала Xk = 11100. Решение: 1. В соответствии с заданным алгоритмом поступления на вход ЦФ (рис. 12), в ЦФ необходимо использовать следующие элементы: два элемента задержки, которые задерживает входной сигнал выборки на один интервал дискретизации; три умножителя – элемента, выполняющего умножение на число; один сумматор – элемент, выполняющий сложение всех сигналов, поступающих на его входы. 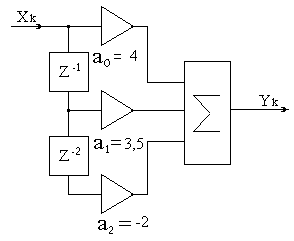 Рисунок 4.1 – Структурная схема нерекурсивного ЦФ для заданного алгоритма 2. В соответствии в дискретной сверткой коэффициенты ak являются значениями дискретной импульсной характеристики hk, то есть: {hk} = {a0, a1, a2} = {4; 3,5; -2}. 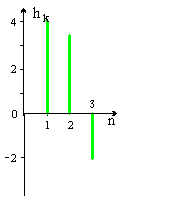 Рисунок 4.2 – Дискретная импульсная характеристика 3. Нахождение системной функции ЦФ. I способ. По определению: 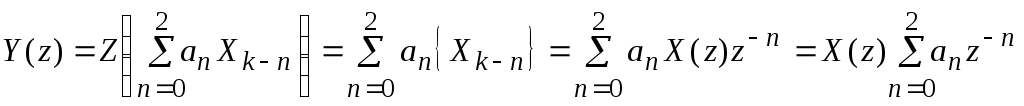 , тогда , тогда 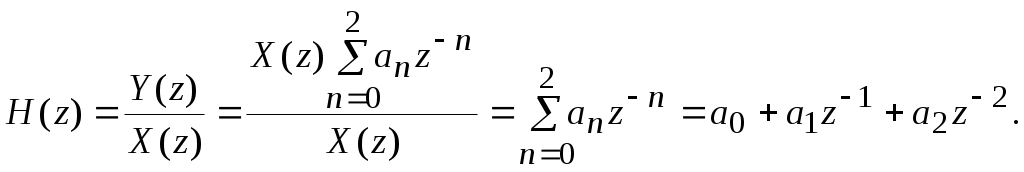 II способ. Операторная передаточная функция H(x) связана с дискретной импульсной характеристикой hk. По свойству Z-преобразованию: При использовании этого свойства находим: 4. Расчет частотного коэффициента передачи ЦФ. 5. Расчет сигнала на выходе ЦФ. На рисунке 13 пунктиром изображен соответствующий ему эквивалент аналогового сигнала. 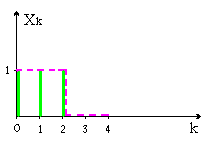 Рисунок 4.3 – Входная последовательность отсчетов {Xk} = (11100) y5 = 0; y6 = 0. 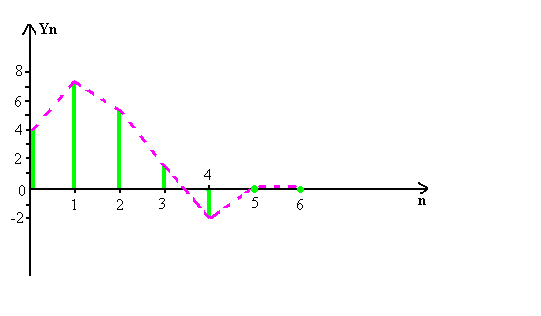 Рисунок 4.4 – Выходная последовательность {yn} Пунктиром изображена временная диаграмма соответствующего ему эквивалента аналогового сигнала. Как видно из сравнения, форма выходного сигнала (рис.4.4), отличается от формы входного (рис. 4.3). Длительность сигнала на выходе из-за элементов задержки в схеме ЦФ больше длительности входного сигнала на количество отсчетов, равное числу элементов задержки, т.е. NВЫХ = NВХ + 2 = 5 + 2 = 7. Список литературы Гарсков Г.Х., Чернецкий Г.А. Математические основы цифровой обработки сигналов: методические указания. – СибГУТИ, Новосибирск, 1999. Чернецкий Г.А. Математические основы цифровой обработки сигналов. Учебное пособие. – СибГУТИ, Новосибирск, 2001. Бизин А.Т. Введение в цифровую обработку сигналов. Учебное пособие. – СибГУТИ, Новосибирск, 1998. Гольденберг Л.М и др. Цифровая обработка сигналов. Учебное пособие для вузов. – Радио и связь, Москва, 1990. Гоноровский И.С. Радиотехнические цепи и сигналы. – Радио и связь, Москва, 1986. | ||||||||||||||||||||||||||||||||||||||||||||||||||||