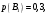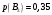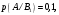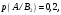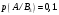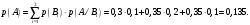|
|
Математика 4 семестр. Тика 2
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Тульский государственный университет»
КОНТРОЛЬНАЯ РАБОТА
4 семестр
ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
2 вариант
Выполнил: ст. Группа ИБ161581 Воробьева М.А
Проверил: Соколова М.Ю.
Тула 2021
1. Вычислить  , если область D ограничена линиями , если область D ограничена линиями 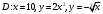 . .
Решение.
Выполним схематический чертеж области интегрирования:
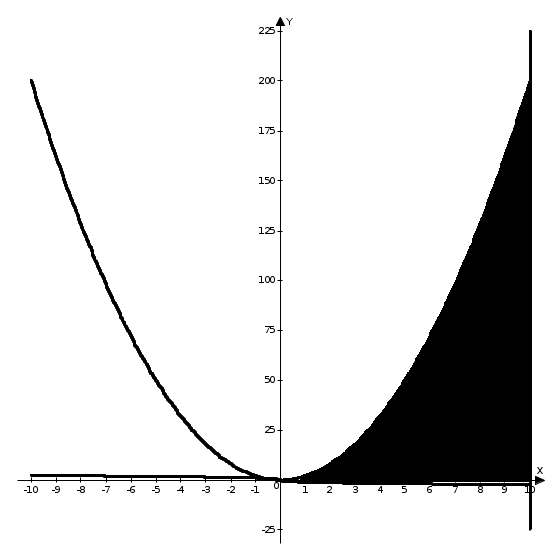
Рисунок 1.
Расставим пределы интегрирования и перейдем к повторному интегралу.
Рассмотрим область  : переменная : переменная 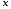 изменяется от 0 до 10, а переменная изменяется от 0 до 10, а переменная 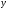 изменяется от кривой изменяется от кривой 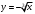 до параболы до параболы 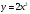 . Тогда . Тогда
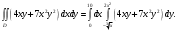
Следовательно,
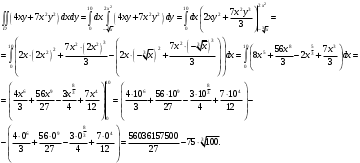 Ответ: Ответ: 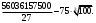
2. Вычислить 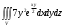 , если область интегрирования ограничена поверхностями , если область интегрирования ограничена поверхностями  . .
Решение.
Проекция заданного тела на плоскость xoy: 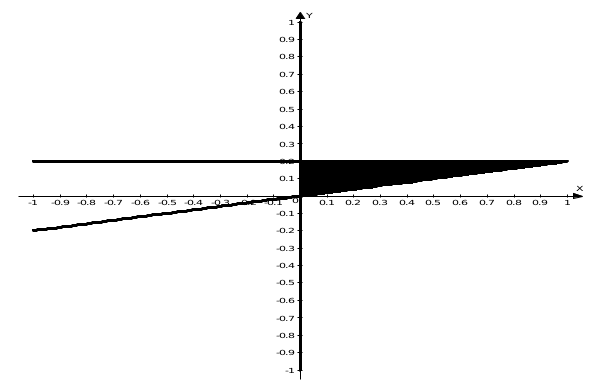
Рассмотрим поверхность 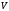 : переменная : переменная  изменяется от изменяется от  до до 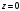 , переменная , переменная  изменяется от изменяется от 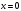 до до  , а переменная , а переменная 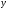 изменяется от изменяется от 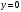 до до 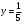 . Тогда: . Тогда:
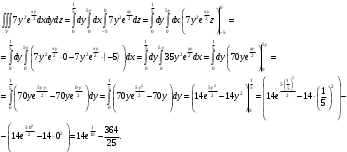
Ответ: 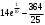 . .
3. Найти площадь фигуры, ограниченной линиями 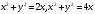 . .
Решение.
Выполним схематический чертеж области интегрирования:
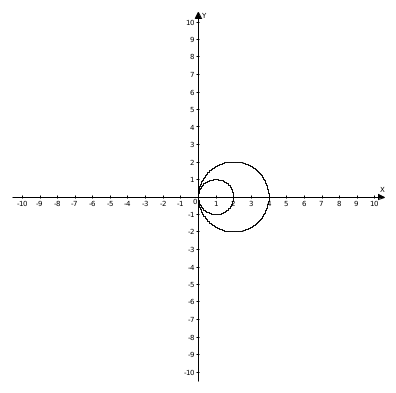
Рисунок 1.
Перейдем к полярной системе координат.
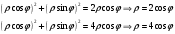 , ,
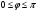 . .
Площадь области в полярных координатах находится по формуле:
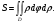
Расставим пределы интегрирования. Переменная  изменяется от 0 до изменяется от 0 до  в это время в это время  изменяется от изменяется от 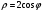 до до  . .
Тогда искомая площадь будет:
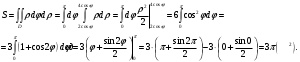
Ответ: 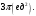
4. Вычислить объем V тела, ограниченного поверхностями
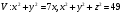 . .
Решение.
Изобразим данное тело и его проекцию на плоскость Оху.


В прямоугольной системе координат объем пространственной замкнутой области равен тройному интегралу по этой замкнутой области от функции, тождественно равной единице, т.е. объем тела равен 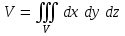 . .
Перейдём в интеграле к цилиндрическим координатам по формулам:
 где где  , , 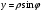 , , 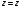 . .
Рассмотрим поверхность  : : 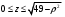 , , 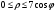 , , 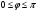 Тогда: Тогда:

Ответ: 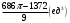 . .
5. Вычислить тройной интеграл  , ,
 . .
Решение.
Для вычисления интеграла перейдем к цилиндрическим координатам по формулам:
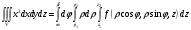 . .
Рассмотрим поверхность 

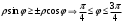
переменная 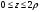 , переменная , переменная 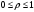 , переменная , переменная 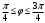 , тогда: , тогда:
 Ответ: Ответ:  . .
6. Вычислить криволинейный интеграл первого рода от функции 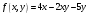 по контуру треугольника с вершинами O(0;0), А(1,5;4,5), В(4,5;1,5). по контуру треугольника с вершинами O(0;0), А(1,5;4,5), В(4,5;1,5).
Решение.
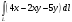 . .
Составим уравнения отрезков треугольника:
 : : 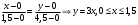 . .
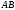 : : 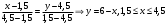 . .
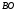 : :  . .
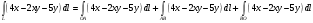 . .
Согласно формуле:
 . .
Находим каждый интеграл:
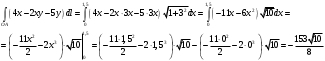
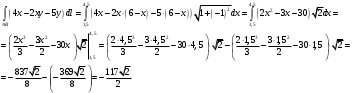
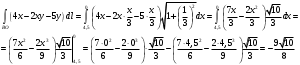
Поэтому
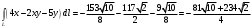
Ответ: 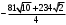 . .
7. Вычислить поверхностный интеграл первого рода 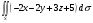 , где S - часть плоскости , где S - часть плоскости 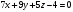 , лежащая в первом октанте. , лежащая в первом октанте.
Решение.
Формула, выражающую интеграл по поверхности S через двойной интеграл по проекции поверхности S на плоскость Oxy , имеет вид:
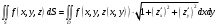 . .
В данном случае поверхность интегрирования S часть плоскости 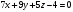 , лежащая в первом октанте. , лежащая в первом октанте.
Из уравнения плоскости: 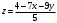 , найдем частные производные: , найдем частные производные: 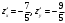 . .
Вычислим дифференциал поверхности по формуле: 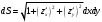 , получим , получим 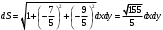 . .
Сведем вычисление поверхностного интеграла к вычислению двойного интеграла по области D, где D – треугольник АОВ, являющийся проекцией поверхности S на координатную плоскость Оху, рис.
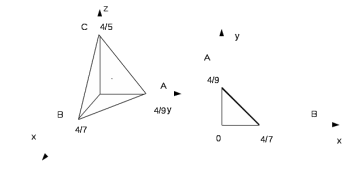
Рис. Рис.
Получим,

Ответ: 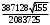 . .
8. Найти косинус угла между градиентами скалярных полей 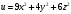 , ,  в точке в точке  . .
Решение.
а) Вычислим градиент скалярного поля 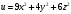 в точке в точке  . Для этого найдем частные производные . Для этого найдем частные производные 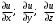 и вычислим их значения в точке и вычислим их значения в точке  . .
 ; ;
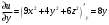 ; ;
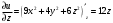 . .
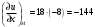 , ,
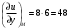 , ,
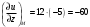 . .
Следовательно, 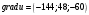 . .
б) Вычислим градиент скалярного поля  в точке в точке  . Найдем частные производные . Найдем частные производные 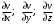 и вычислим их значения в точке и вычислим их значения в точке  . .
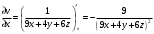 ; ;
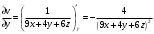 ; ;
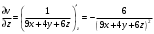 . .
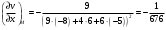 , ,
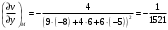
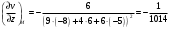 . .
Значит, 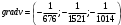 . .
в) Так как градиент – это вектор, то угол между градиентами скалярных полей найдем по формуле: 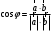 . .
Тогда
 . .
Ответ:  . .
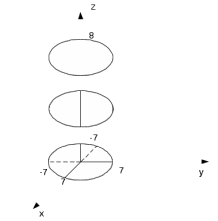
9. Найти поток векторного поля 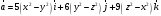 через замкнутую поверхность через замкнутую поверхность 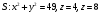 в направлении внешней нормали. в направлении внешней нормали.
Решение.
Для вычисления потока воспользуемся формулой Остроградского-Гаусса, т.к. поверхность замкнутая :
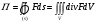 . .
Находим дивергенцию:
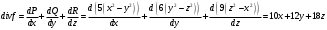 . .
переходим к цилиндрическим координатам:  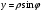 
Тогда:
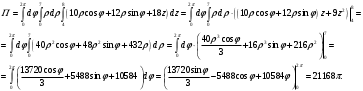 Ответ: Ответ: 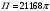
10. Найти работу силы 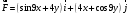 при перемещении от точки O(0;0) до точки при перемещении от точки O(0;0) до точки  по дуге линии по дуге линии 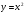 . .
Решение.
Пусть 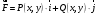 есть переменная сила, совершающая работу A есть переменная сила, совершающая работу A
вдоль пути L , и функции 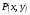 и и 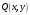 непрерывны на кривой L . Тогда непрерывны на кривой L . Тогда
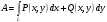 . В данной задаче: . В данной задаче:
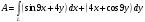 . .
Находим: 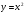 , , 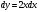 . .
Получаем:
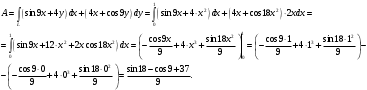 Ответ: Ответ: 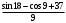 . .
11. В урне находятся 3 белых и 7 черных шаров. Из урны извлекаются 2 шара. Какова вероятность того, что среди них один белый шар.
Решение.
Общее число выбора 2 шаров из 3+7=10 равно числу сочетаний из 10 по 2, т.е. 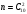 . .
Число благоприятных случаев равно числу выбора 1 белого шара из 3,  умноженному на число выбора 1 черного шаров из 7, умноженному на число выбора 1 черного шаров из 7, 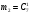 , т.е. , т.е. 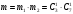 . .
По классическому определению вероятности получаем:
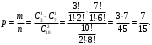
Ответ: 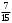 . .
12. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что хотя бы в одном из них допущенная ошибка превысит заданную точность.
Решение.
Так как появление ошибки, превышающей заданную точность независим друг от друга, то для вычисления вероятностей используется формула Бернулли:
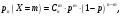 где где 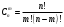 – число сочетаний из n элементов по m, m– число благоприятных исходов, n– общее число опытов, p– вероятность наступления данного события при одном опыте. – число сочетаний из n элементов по m, m– число благоприятных исходов, n– общее число опытов, p– вероятность наступления данного события при одном опыте.
Пусть А– событие при трех измерениях хотя бы в одном из них допущенная ошибка превысит заданную точность. Противоположным для заданного события будет событие  , состоящее в том, что ни в одном из измерений допущенная ошибка не превысит заданную точность. , состоящее в том, что ни в одном из измерений допущенная ошибка не превысит заданную точность.
Тогда:
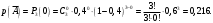
Для противоположных событий имеет место формула:
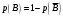 , тогда: , тогда:
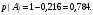
Ответ: 0,784.
13. На складе находятся 30 деталей, из которых 19 стандартные. Рабочий берет наугад две детали. Определить вероятность того, что обе детали окажутся стандартными.
Решение.
Общее число выбора 2 деталей из 30 равно числу сочетаний из 30 по 2, т.е. 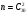 . .
Общее число выбора 2 стандартных деталей из 19 равно числу сочетаний из 19 по 2, т.е.  . .
По классическому определению вероятности получаем:

Ответ: 0,3931.
14. Часы изготавливаются на трех заводах и поступают в магазин. Первый завод производит 30% продукции, второй – 35%, третий – 35%. В продукции первого завода спешат 10% часов, второго – 20% и третьего – 10%. Найти вероятность того, что купленные часы спешат.
Решение.
Пусть А событие, состоящее в том, что купленные часы спешат – может произойти совместно с одним из событий-гипотез – часы с первого завода (В1), часы со второго завода (B2), часы с третьего завода (B3). Тогда вероятности:
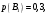  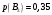
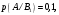 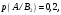 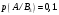
По формуле полной вероятности получаем вероятность
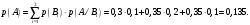
Ответ: 0,135.
15. Дано следующее распределение дискретной случайной величины Х
Х
|
-1
|
1
|
3
|
4
|
10
|
Р
|
0,3
|
0,2
|
0,2
|
0,14
|
0,16
|
Найти ее математическое ожидание, дисперсию и среднеквадратичное отклонение.
Решение.
Математическое ожидание 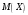 дискретной случайной величины Х найдем по формуле: дискретной случайной величины Х найдем по формуле:
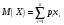 . .
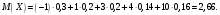
Дисперсию 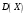 дискретной случайной величины Х найдем по формуле: дискретной случайной величины Х найдем по формуле:
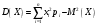 . .

Среднее квадратическое отклонение 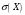 дискретной случайной величины Х найдем по формуле: дискретной случайной величины Х найдем по формуле:
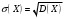 . .

Ответ:  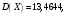 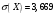 . . |
|
|
 Скачать 0.49 Mb.
Скачать 0.49 Mb. , если область D ограничена линиями
, если область D ограничена линиями 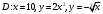 .
.
 : переменная
: переменная 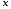 изменяется от 0 до 10, а переменная
изменяется от 0 до 10, а переменная 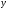 изменяется от кривой
изменяется от кривой 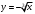 до параболы
до параболы 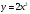 . Тогда
. Тогда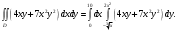
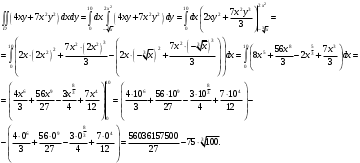 Ответ:
Ответ: 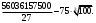
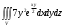 , если область интегрирования ограничена поверхностями
, если область интегрирования ограничена поверхностями  .
.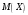 дискретной случайной величины Х найдем по формуле:
дискретной случайной величины Х найдем по формуле: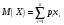 .
.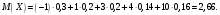
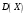 дискретной случайной величины Х найдем по формуле:
дискретной случайной величины Х найдем по формуле: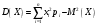 .
.
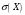 дискретной случайной величины Х найдем по формуле:
дискретной случайной величины Х найдем по формуле: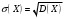 .
.

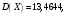
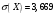 .
.
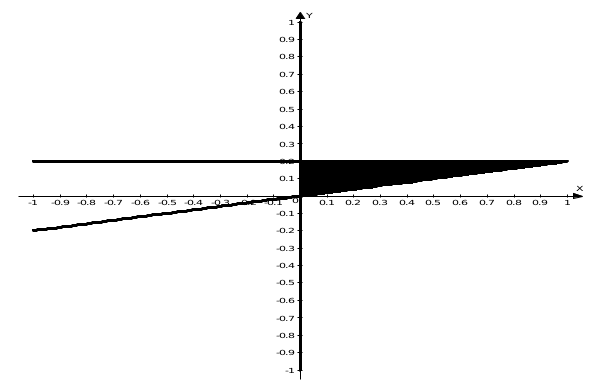
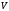 : переменная
: переменная  изменяется от
изменяется от  до
до 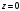 , переменная
, переменная  изменяется от
изменяется от 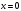 до
до  , а переменная
, а переменная 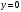 до
до 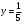 . Тогда:
. Тогда: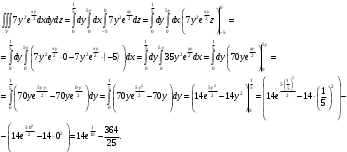
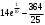 .
.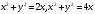 .
.
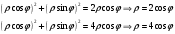 ,
, 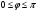 .
.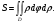
 изменяется от 0 до
изменяется от 0 до  в это время
в это время  изменяется от
изменяется от 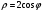 до
до  .
.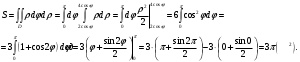
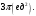
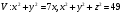 .
.

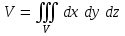 .
. где
где  ,
, 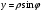 ,
, 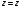 .
.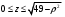 ,
, 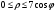 ,
, 
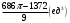 .
. ,
,  .
.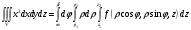 .
.
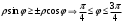
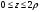 , переменная
, переменная 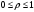 , переменная
, переменная 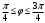 , тогда:
, тогда: Ответ:
Ответ:  .
.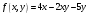 по контуру треугольника с вершинами O(0;0), А(1,5;4,5), В(4,5;1,5).
по контуру треугольника с вершинами O(0;0), А(1,5;4,5), В(4,5;1,5). 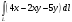 .
. :
: 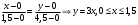 .
.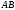 :
: 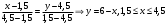 .
.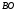 :
:  .
.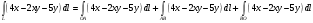 .
. .
.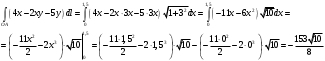
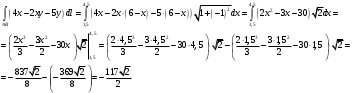
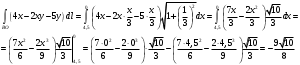
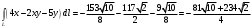
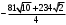 .
.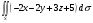 , где S - часть плоскости
, где S - часть плоскости 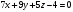 , лежащая в первом октанте.
, лежащая в первом октанте.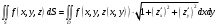 .
.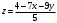 , найдем частные производные:
, найдем частные производные: 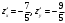 .
.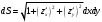 , получим
, получим 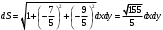 .
.

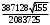 .
.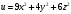 ,
,  в точке
в точке  .
.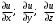 и вычислим их значения в точке
и вычислим их значения в точке  ;
; 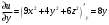 ;
;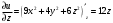 .
.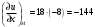 ,
, 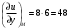 ,
, 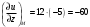 .
.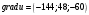 .
. и вычислим их значения в точке
и вычислим их значения в точке 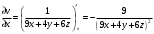 ;
; 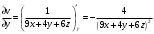 ;
;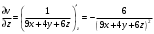 .
.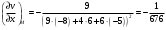 ,
,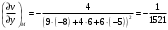
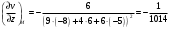 .
.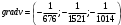 .
.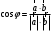 .
.  .
. .
.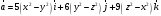 через замкнутую поверхность
через замкнутую поверхность 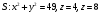 в направлении внешней нормали.
в направлении внешней нормали. 
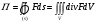 .
.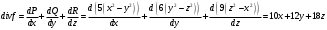 .
.
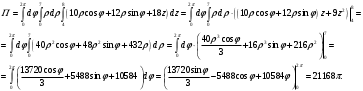 Ответ:
Ответ: 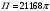
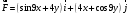 при перемещении от точки O(0;0) до точки
при перемещении от точки O(0;0) до точки  по дуге линии
по дуге линии 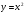 .
.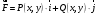 есть переменная сила, совершающая работу A
есть переменная сила, совершающая работу A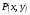 и
и 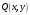 непрерывны на кривой L . Тогда
непрерывны на кривой L . Тогда 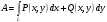 . В данной задаче:
. В данной задаче: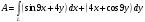 .
.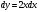 .
.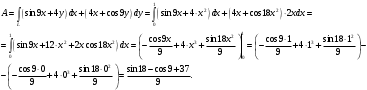 Ответ:
Ответ: 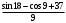 .
.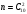 .
. умноженному на число выбора 1 черного шаров из 7,
умноженному на число выбора 1 черного шаров из 7, 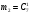 , т.е.
, т.е. 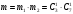 .
.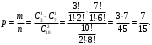
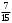 .
.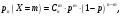 где
где 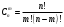 – число сочетаний из n элементов по m, m– число благоприятных исходов, n– общее число опытов, p– вероятность наступления данного события при одном опыте.
– число сочетаний из n элементов по m, m– число благоприятных исходов, n– общее число опытов, p– вероятность наступления данного события при одном опыте. , состоящее в том, что ни в одном из измерений допущенная ошибка не превысит заданную точность.
, состоящее в том, что ни в одном из измерений допущенная ошибка не превысит заданную точность.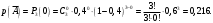
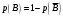 , тогда:
, тогда: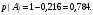
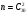 .
. .
.