лаба по лестридчеству. Лабораторная работа 2. Транспортная задача сведения из теории

• Название: Транспортная задача сведения из теории
• Анкор: лаба по лестридчеству
• Дата: 04.10.2022
• Размер: 364 Kb.
• Имя файла: Лабораторная работа 2.doc
• Тип: Задача; #713906

ТРАНСПОРТНАЯ ЗАДАЧА

3.2. Сведения из теории

Планирование перевозок грузов является важной экономической задачей, занимающей ключевое место среди других проблем планирования. Большое значение имеет задача о минимизации транспортных издержек при перевозках однородных грузов из пунктов производства в пункты потребления, например, древесины с нижних складов к деревообрабатывающим предприятиям, строительных материалов с баз на стройплощадки и т.п.

Пусть поставщиков располагают единицами некоторого однородного продукта (груза), и этот продукт должен быть доставлен потребителям в количествах соответственно. Известны стоимости , , перевозки единицы груза от поставщика потребителю . Следует определить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий наименьшие суммарные транспортные затраты.

Модель транспортной задачи называется закрытой (или сбалансированной), если суммарные запасы груза равны суммарным потребностям, т.е.

.
Если это условие не выполняется, то модель называется открытой (или несбалансированной). Открытая модель легко сводится к закрытой путем введения фиктивного поставщика (если потребности превышают запасы) или фиктивного потребителя (если запасы превышают потребности). Поэтому мы ограничимся рассмотрением только закрытой модели.

План перевозок транспортной задачи можно представить в виде матрицы , где – количество единиц груза, перевозимого от поставщика потребителю , , . Естественно предполагать, что .

Стоимость перевозки груза от к составит .

Следовательно, суммарные транспортные расходы по плану составят

. (3.1)

Система ограничений получается из следующих соображений. Все запасы из пункта должны быть вывезены, т.е.

, . (3.2)

Все потребности пункта должны быть удовлетворены, т.е.

, . (3.3)

Таким образом, математическая модель транспортной задачи состоит в определении неотрицательного плана перевозок , для которого выполняются условия (3.2) и (3.3), а целевая функция (3.1) принимает наименьшее значение. Доказано, что транспортная задача с закрытой моделью всегда разрешима, т.е. она имеет оптимальное решение.

Специфика ограничений транспортной задачи значительно облегчает применение симплексного метода для ее решения. Симплексный метод сводится к методу потенциалов, при использовании которого можно обойтись без составления симплексных таблиц, заменив их таблицами перевозок вида табл. 3.1.

Т а б л и ц а 3.1

Пункты отправления и запасы груза		Пункты назначения и потребности
						…
						…
						…
						…
…	…	…		…		…	…
						…

3.3. Пример выполнения работы
Предположим, что запасы груза в пунктах отправления равны соответственно A1, A2 и A3 единиц. Потребности пунктов назначения составляют соответственно B1, B2, B3, B4, B5 единиц. Затраты на перевозку единицы груза (тарифы) содержатся в матрице C

Вариант 1,7,13 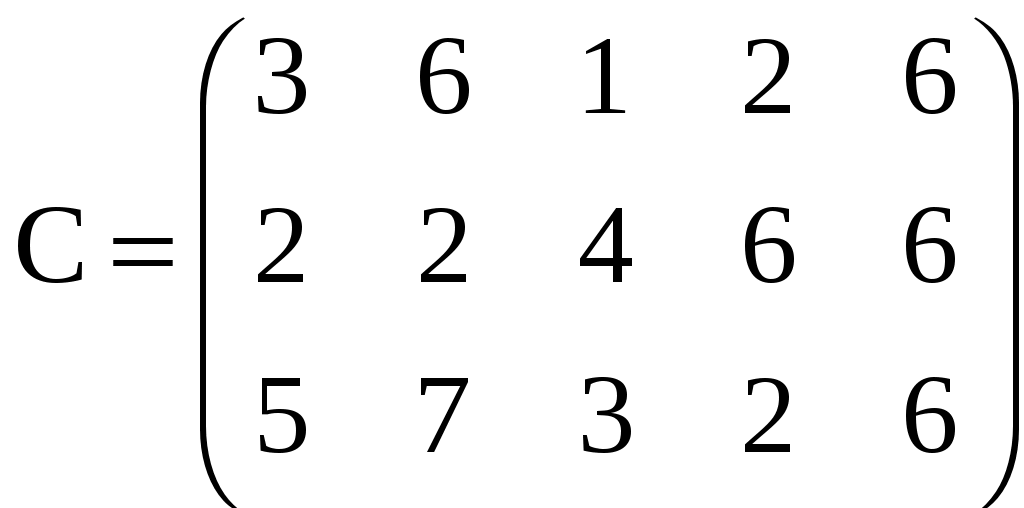. A: (160, 200 , 80) ;
B: (100, 120, 110, 60, 50)
Вариант 2,8,14 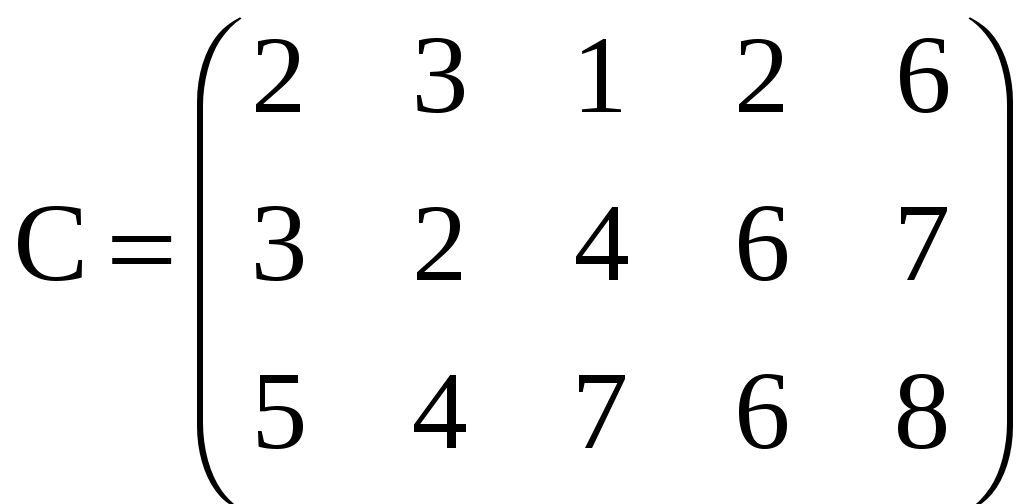A: (200, 100 , 140) ;
B: (100, 40, 100, 70, 130)

Вариант 3,9,15 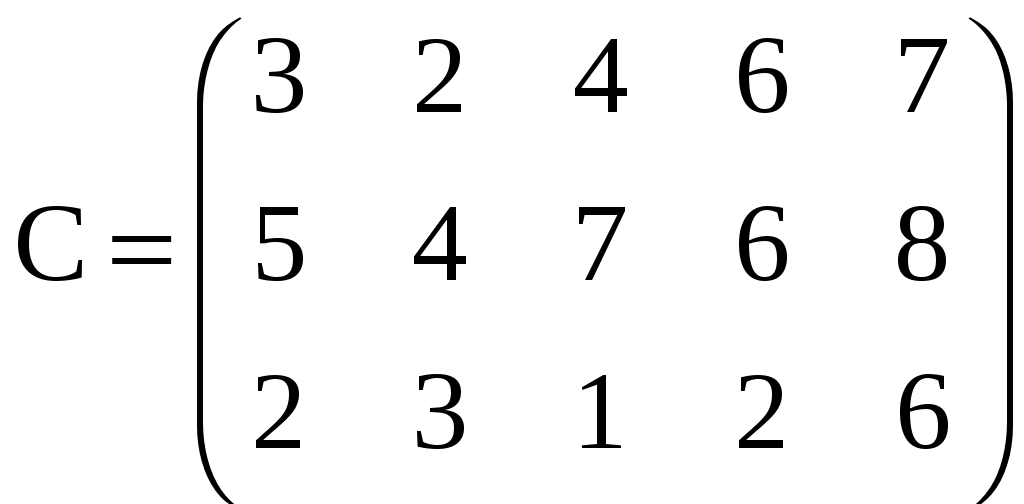A: (220, 100 , 120) ;
B: (70, 100, 110, 100, 60)

Вариант 4,10,16 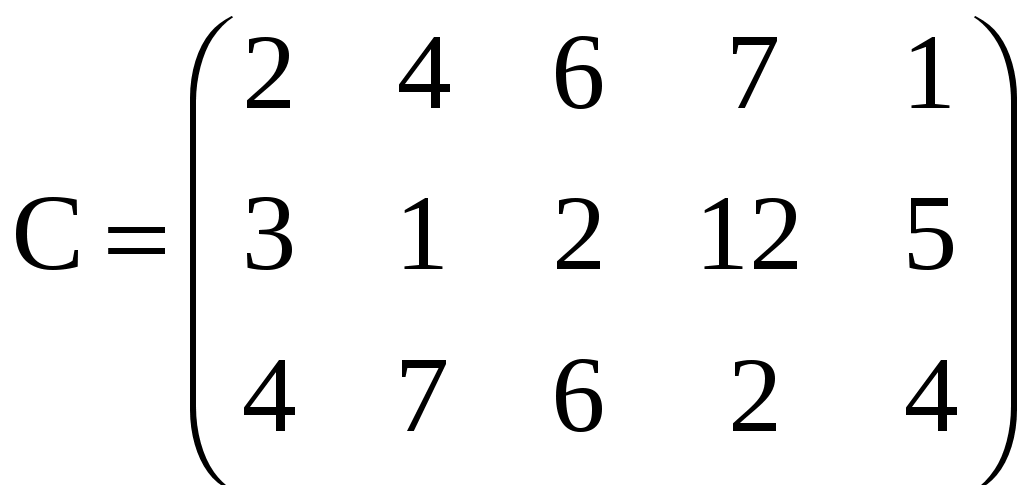A: (150, 100 , 190) ;
B: (100, 70, 40, 120, 110)
Вариант 5,11,17 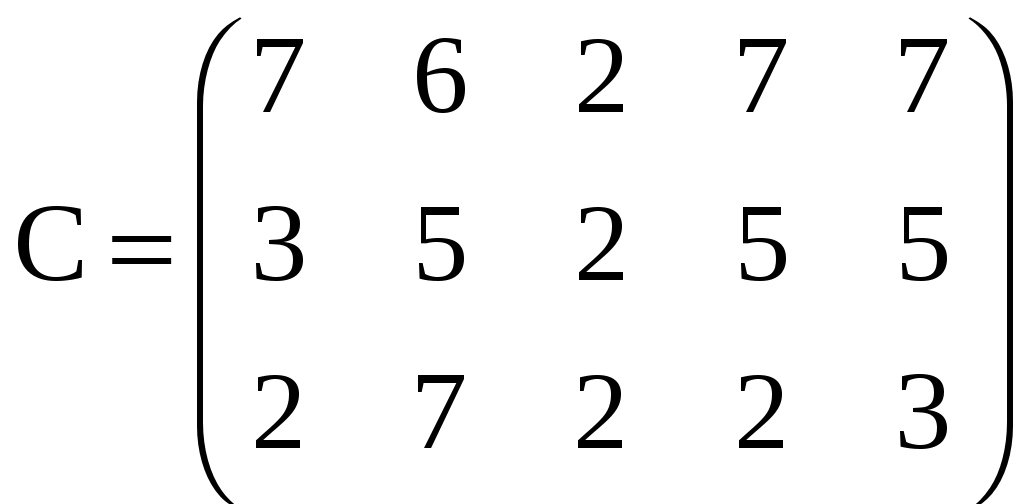A: (140, 180 , 120) ;
B: (50, 100, 100, 70,120)

Вариант 6,12,18 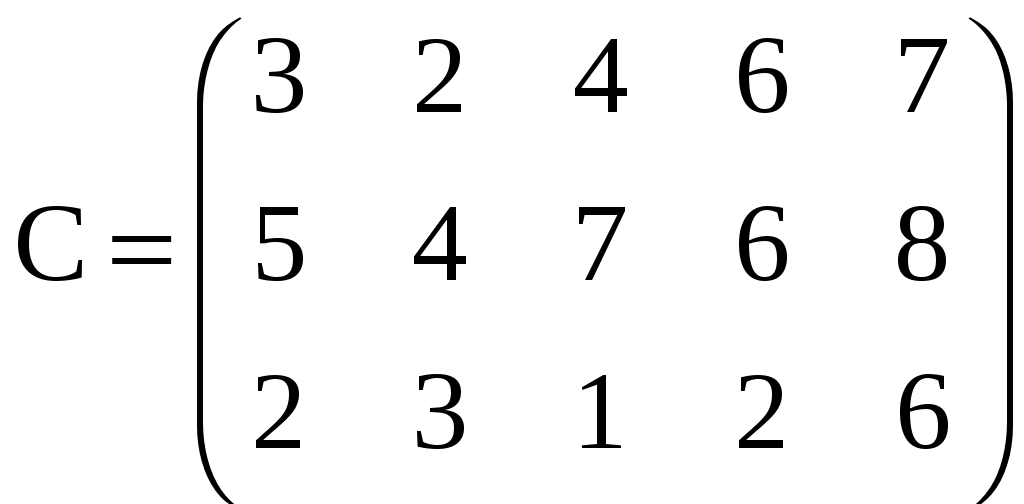A: (150, 100 , 190);
B: (100, 120, 110, 60, 50)

3.3.1. Таблица перевозок

Имеем транспортную задачу с тремя поставщиками и пятью потребителями, исходные данные которой можно представить в виде табл. 3.2.

Т а б л и ц а 3.2

Пункты отправления и запасы груза		Пункты назначения и потребности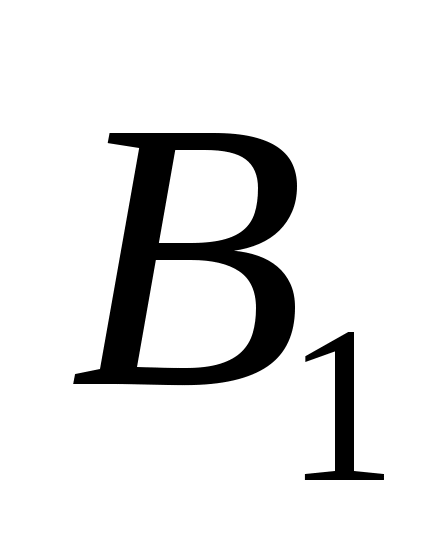
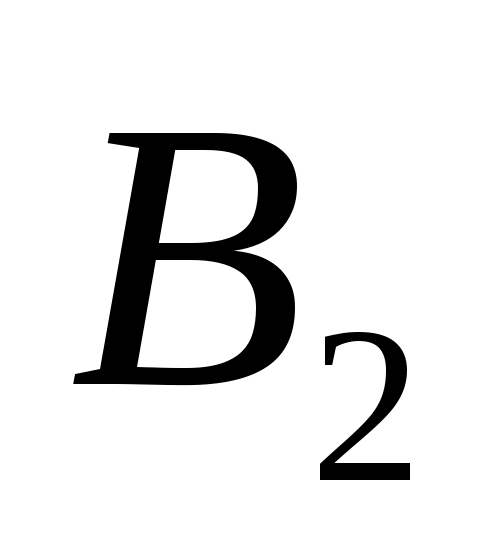
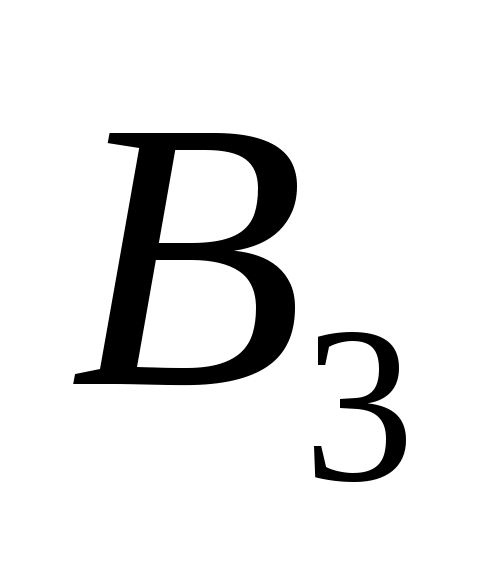
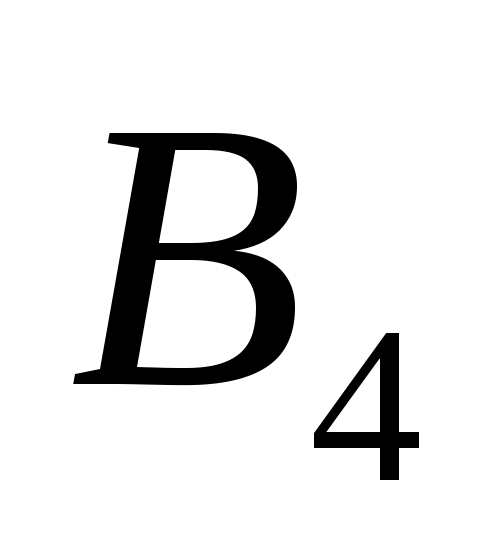
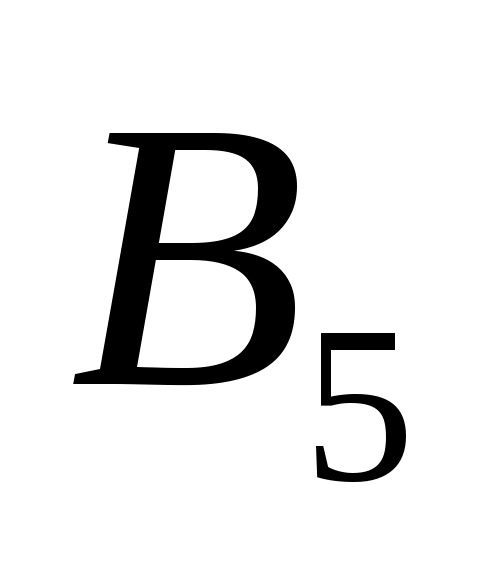
		120		100		110		70		40
	200		3		2		4		6		7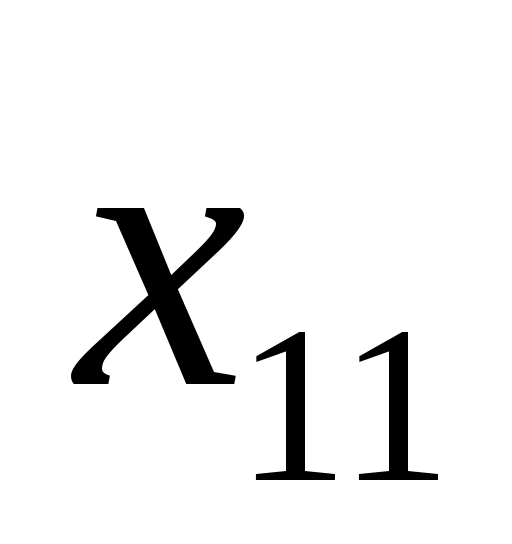
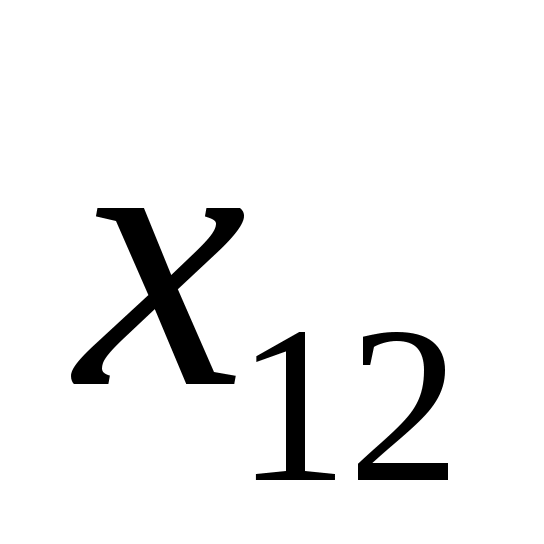
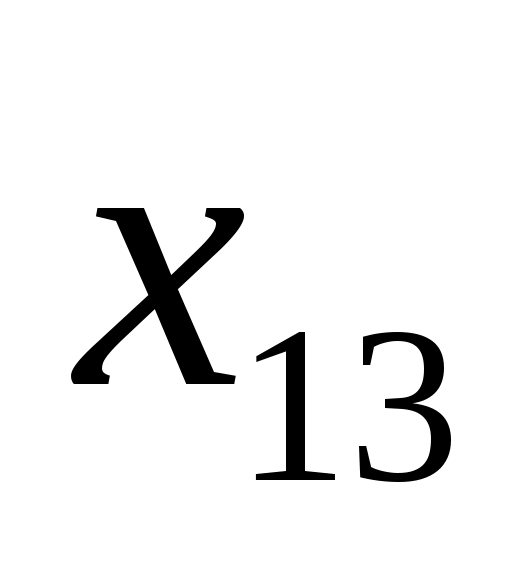
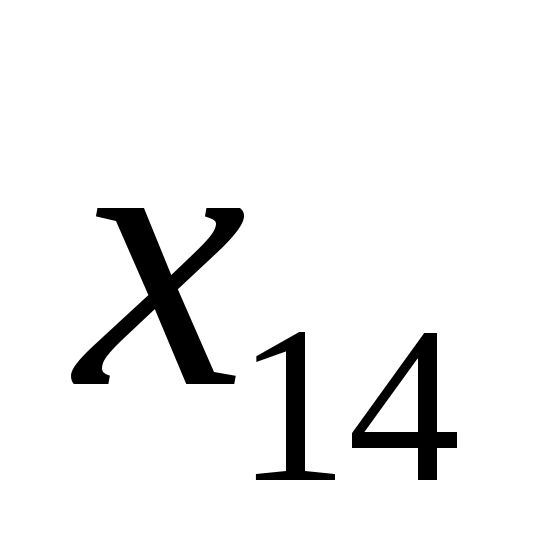
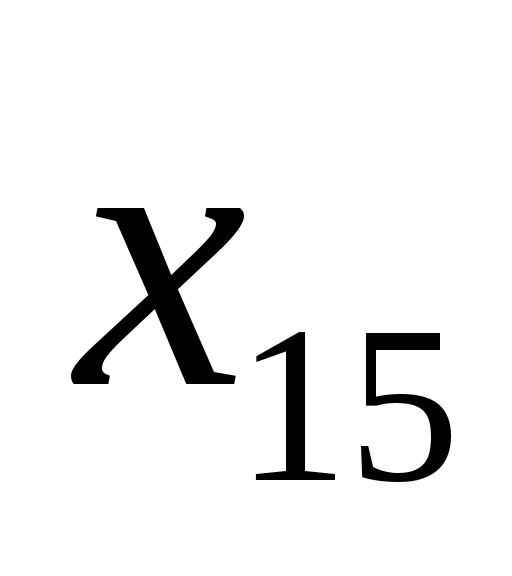
	160		2		3		1		2		6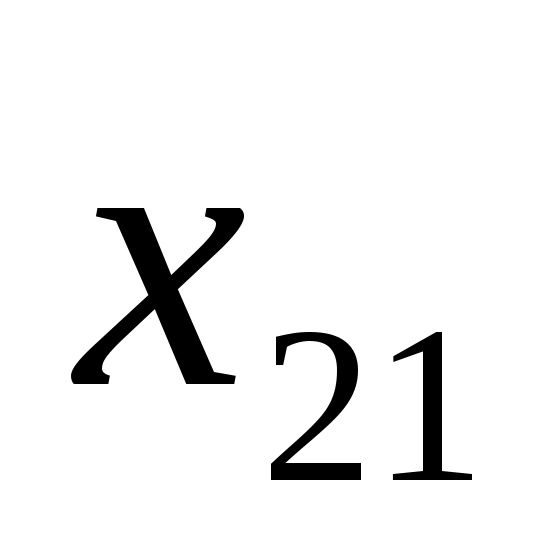
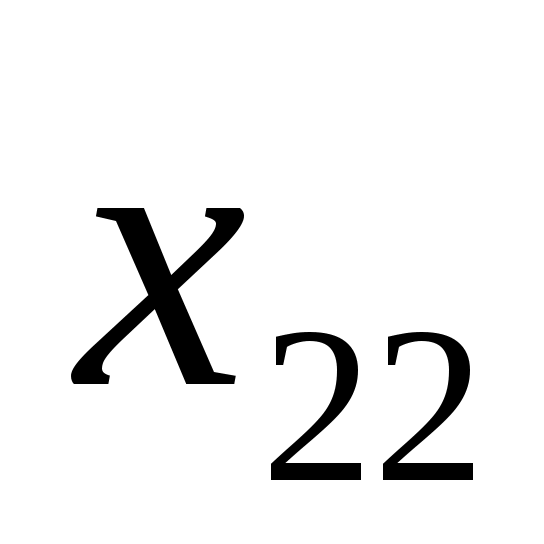
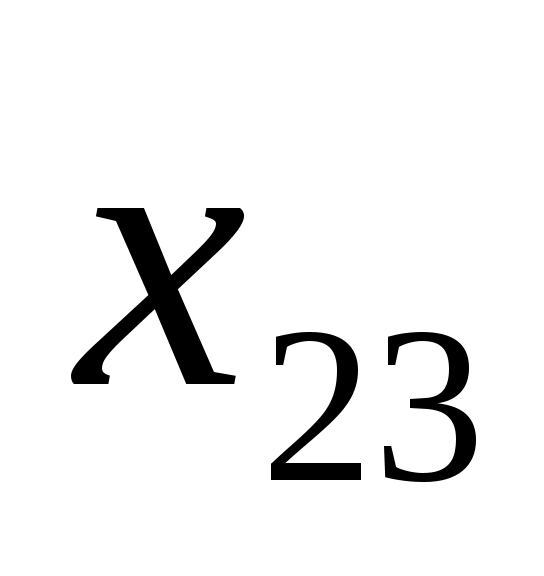
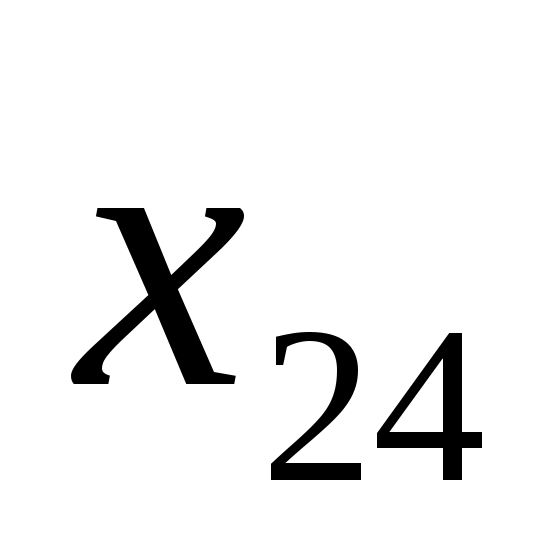
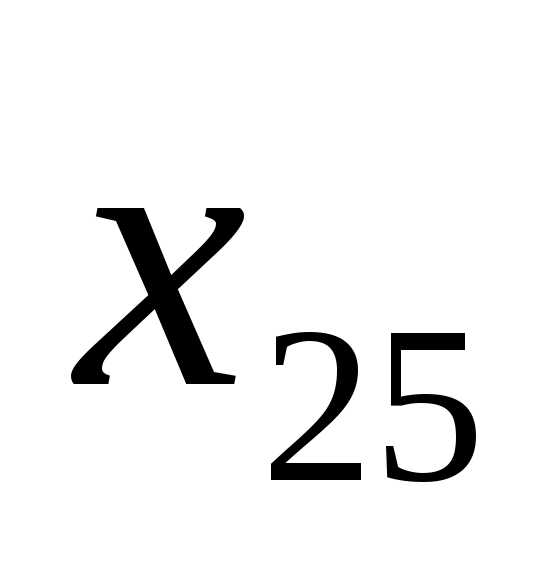
	80		5		4		7		6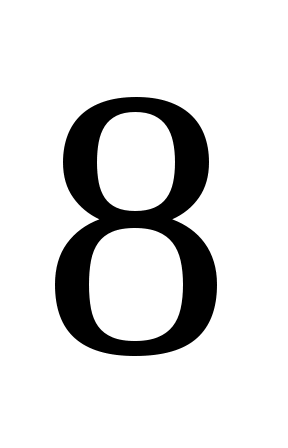

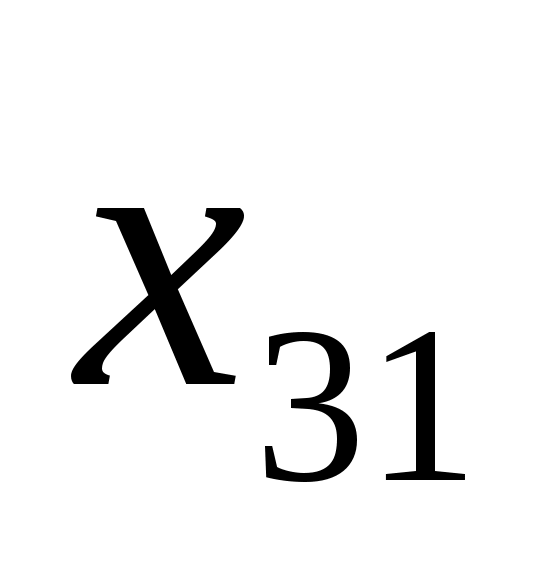
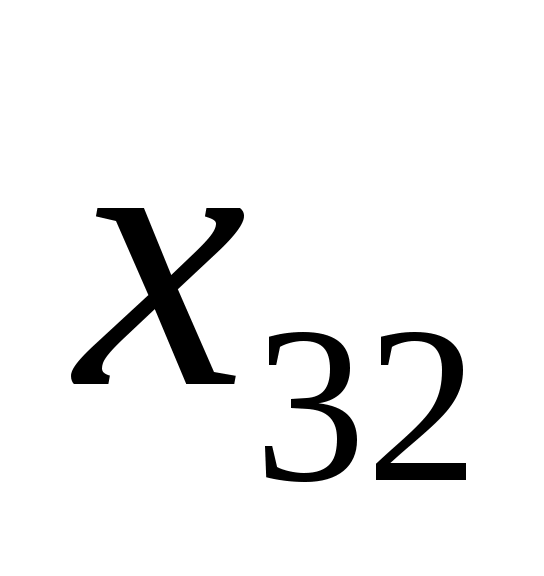
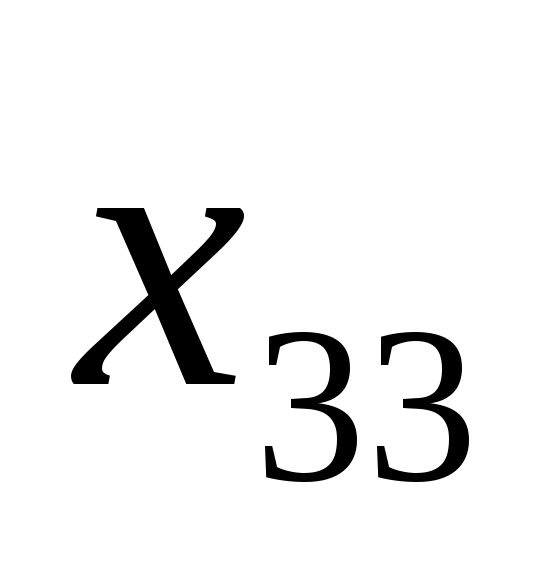
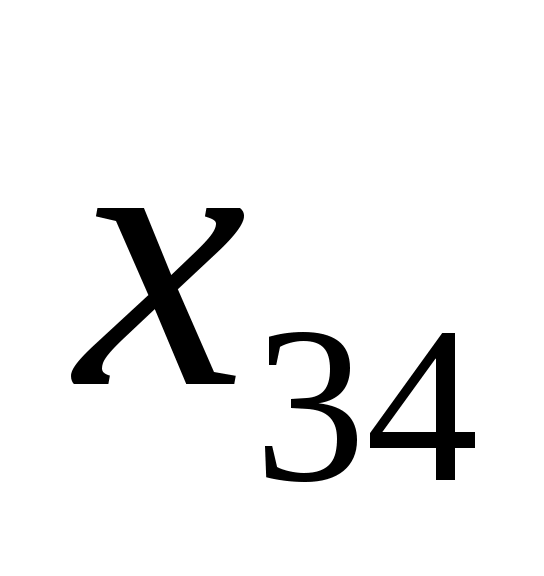
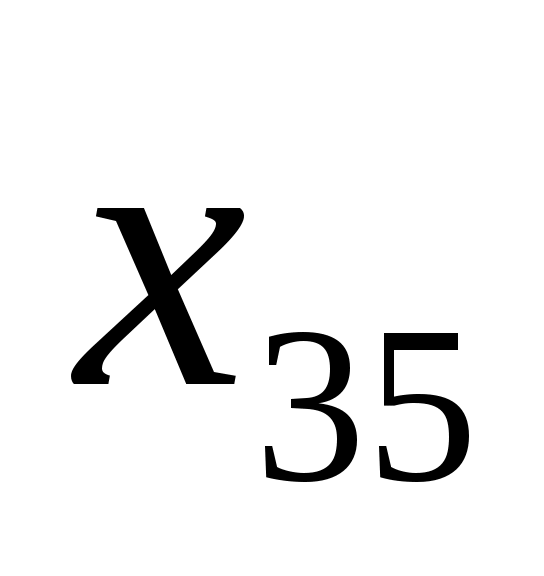
3.3.2. Математическая модель

Определим сначала вид транспортной модели. Для этого вычислим сумарные запасы груза у поставщиков



и суммарные потребности

.

Так как , то модель является закрытой, и задача обязательно имеет оптимальное решение.

Суммарные транспортные затраты на перевозки груза от поставщиков к потребителям согласно (3.1) составляют

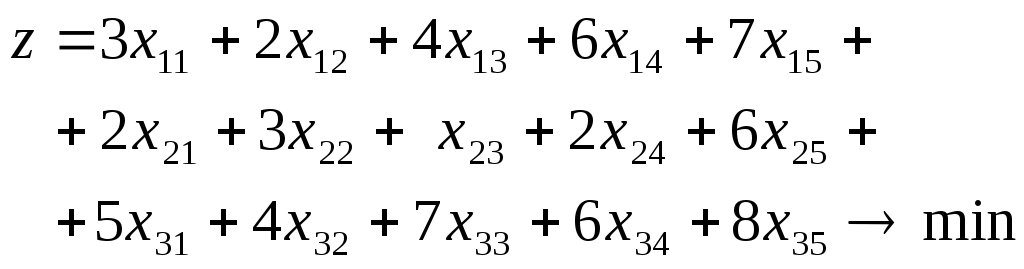. (3.4)

Ограничения (3.2) и (3.3) показывают, что все запасы должны быть вывезены от поставщиков

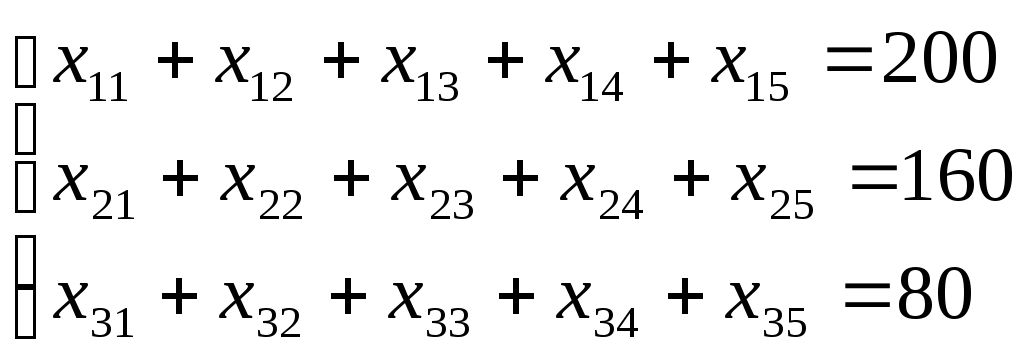(3.5)

и должны быть удовлетворены потребности пунктов назначения

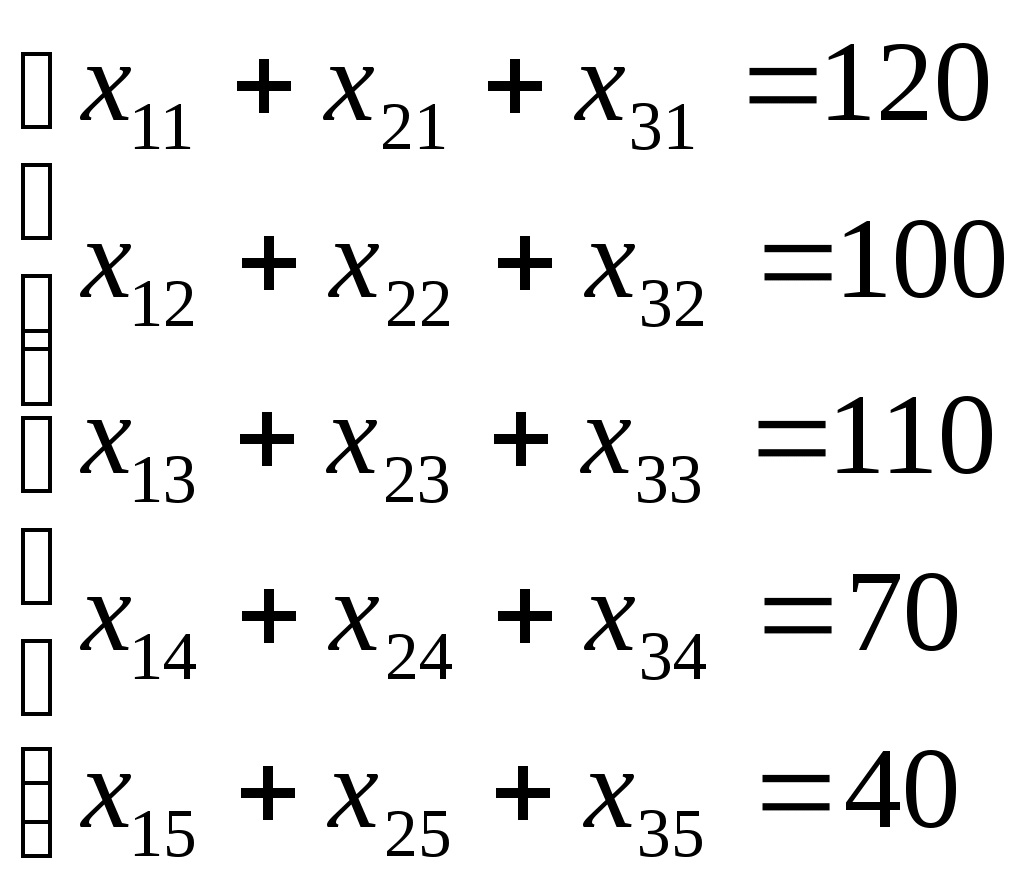. (3.6)

Все поставки груза должны быть неотрицательными

, , . (3.7)

Соотношения (3.4)-(3.7) обрауют математическую модель транспортной задачи.

Замечание. Одно из уравнений системы (3.5)-(3.6) следует из остальных уравнений, и его можно опустить. Действительно, если сложить все уравнения (3.5) и из полученной суммы вычесть любые четыре уравнения системы (3.6), то получим пятое уравнение этой системы. Таким образом, одно из уравнений системы ограничений является линейной комбинацией остальных уравнений.
3.3.3. «Равномерный» план перевозок

В среде Excel на листе 1 в блоке ячеек B2 : F4 поместим тарифы на перевозки из табл. 3.2. Блок ячеек B7 : F9 предусмотрим для записи плана перевозок. В ячейки H7 : H9 запишем запасы груза у поставщиков, а в ячейки B11 : F11 – потребности пунктов назначения. Суммарные затраты на перевозку будем рассчитывать в ячейке G2, в которую поместим формулу

= СУММПРОИЗВ(B2 : F4; B7 : F9). Содержимое этой ячейки сначала равно нулю. Однако, постепенно заполняя ячейки B7 : F9 числами, содержимое ячейки G2 будет меняться в соответствии с формулой (3.2).

Чтобы получить «равномерный» план перевозок, запасы поставщика разделим примерно поровну между потребителями. В данном случае направим от каждому потребителю по ед. груза. Тем самым потребитель получит груз в нужном объеме, и тогда поставки от других поставщиков будут нулевыми. Распределяя «равномерно» запасы поставщика между оставшимися потребителями, видим, что каждому следует направить по 40 ед. груза. Однако, потребителю достаточно направить лишь 30 ед., что и записывается в соответствующей клетке. Остальной груз в объеме 130 ед. распределяем так, как это показано в табл.3.3. В строку, соответствующую поставкам , поместим остаточные значения объемов груза.

Т а б л и ц а 3.3

	A	B	C	D	E	F	G	H
1		Тарифы на перевозку груза
2		3	2	4	6	7	1610
3		2	3	1	2	6
4		5	4	7	6	8
5		"Равномерный" план перевозок
6		B1	B2	B3	B4	B5		Запасы
7	A1	40	40	40	40	40		200
8	A2	40	40	50	30	0		160
9	A3	40	20	20	0	0		80
10
11	Потребности	120	100	110	70	40

После заполнения перевозок в клетке G2 мы автоматически получим суммарные затраты, равные 1610 руб.
3.3.4. План перевозок, полученный методом «северо-западного» угла

Следующий план перевозок получим в Excel на листе 2. Отличие от предыдущего плана состоит только в заполнении блока ячеек B7 : F9. Поэтому можно скопировать лист 1 на лист 2 и изменить только содержимое указанного блока. В ячейку B7 («северо-западная» клетка) поставим максимально допустимую перевозку, равную . Тогда перевозки в пункт от других поставщиков должны быть равны нулю. Первый столбец оказался заполненным. Переходим к заполнению следующей «северо-западной» клетки C7, учитывая, что запас поставщика уменьшился на 120 и стал равен 80 ед. В ячейку C7 поставим перевозку, равную . Тогда перевозки из пункта остальным потребителям должны быть равны нулю. Первая строка оказалась заполненной. При этом потребность пункта уменьшилась на величину 80 ед. и стала равной 20 ед. Продолжая этот процесс дальше, получим план перевозок, представленный в табл. 3.4.

Т а б л и ц а 3.4

	A	B	C	D	E	F	G	H
1		Тарифы на перевозку груза
2		3	2	4	6	7	1310
3		2	3	1	2	6
4		5	4	7	6	8
5		План по методу «северо-западного» угла
6		B1	B2	B3	B4	B5		Запасы
7	A1	120	80	0	0	0		200
8	A2	0	20	110	30	0		160
9	A3	0	0	0	40	40		80
10
11	Потребности	120	100	110	70	40

После заполнения перевозок методом «северо-западного» угла в клетке G2 получим суммарные затраты для этого плана, равные 1310 руб.
3.3.5. План перевозок, полученный методом минимальной стоимости

На листе 3 составим план перевозок методом минимальной стоимости. Отличие от предыдущих планов состоит только в заполнении блока ячеек B7 : F9. Заполнение плана перевозок начнем с ячейки, имеющей минимальную стоимость, а именно, с ячейки D8, в которой тариф (ячейка D3) равен 1. В ячейку D8 поместим максимально допустимую перевозку, равную . Поскольку потребность пункта будет удовлетворена, то перевозки в этот пункт от других поставщиков будут равны нулю. Тем самым оказывается заполненным третий столбец, а запас поставщика уменьшится на 110 и составит 160 – 110 = 50 ед. Из оставшихся незаполненных ячеек выбираем новую ячейку с минимальной стоимостью. Пусть это будет C7, у которой тариф равен 2. В ячейку C7 поместим перевозку, равную ед., и тогда в ячейки C8 – C9 ставим нулевые перевозки. Заполненным оказывается второй столбец, а запас поставщика уменьшится на 100 ед. и составит 200 – 100 = 100 ед.

Продолжая этот процесс дальше, получим план перевозок, представленный в табл. 3.5.

Т а б л и ц а 3.5

	A	B	C	D	E	F	G	H
1		Тарифы на перевозку груза
2		3	2	4	6	7	1360
3		2	3	1	2	6
4		5	4	7	6	8
5		План по методу минимальной стоимости
6		B1	B2	B3	B4	B5		Запасы
7	A1	70	100	0	30	0		200
8	A2	50	0	110	0	0		160
9	A3	0	0	0	40	40		80
10
11	Потребности	120	100	110	70	40

После заполнения перевозок методом минимальной стоимости в клетке G2 получим суммарные затраты для этого плана, равные 1360 руб.
3.3.6. Определение оптимального плана перевозок

Планы перевозок груза, полученные ранее и содержащиеся в табл. 3.3-3.5, образованы без привлечения надлежащего математического аппарата, и потому, вряд ли являются оптимальными. Лучшим, т.е. наиболее близким к оптимальному, из трех рассмотренных планов является в данном случае план, полученный методом «северо-западного» угла, так как суммарные затраты по нему наименьшие и составляют 1310 руб.

Оптимальный план перевозок определим в Excel на листе 4 с помощью процедуры «Поиск решения». Скопируем один из предыдущих листов на лист 4 и дополним его двумя графами. В блок ячеек G7 : G9 поместим левые части системы (3.5). Для этого в ячейку G7 поместим формулу

= СУММ(B7 : F7),

которую протянем на ячейки G8 и G9. В блок ячеек B10 : F10 поместим левые части системы (3.6). Для этого в ячейку B10 поместим формулу

= СУММ(B7 : B9),

которую протянем на блок ячеек C10 : F10. Чтобы определить оптимальный план перевозок, следует обратиться к процедуре «Поиск решения», как показано на рис. 3.1.


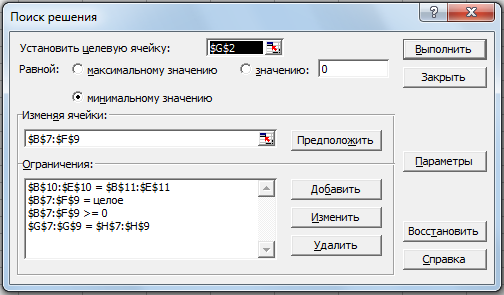
Рис.3.1. Обращение к процедуре «Поиск решения» в транспортной задаче
Согласно сделанному выше замечанию, последнее уравнение системы (3.6) опущено. Кроме того, если будет получено не целочисленное решение, то можно ввести дополнительное ограничение на целочисленность. Результаты оптимизации представлены табл. 3.6.

Т а б л и ц а 3.6

	A	B	C	D	E	F	G	H
1		Тарифы на перевозку груза
2		3	2	4	6	7	1250
3		2	3	1	2	6
4		5	4	7	6	8
5		Оптимальный план перевозок
6		B1	B2	B3	B4	B5		Запасы
7	A1	120	80	0	0	0	200	200
8	A2	0	0	110	50	0	160	160
9	A3	0	20	0	20	40	80	80
10		120	100	110	70	40
11	Потребности	120	100	110	70	40

В ячейке G2 находятся минимальные суммарные затраты для оптимального плана перевозок, составляющие 1250 руб.
3.3.7. Граф перевозок

На основании оптимального плана изображен граф перевозок в виде рис. 3.2. На графе представлены направления перевозок груза и оптимальные объемы перевозок.





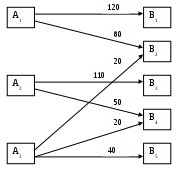
Рис. 3.2. Граф перевозок для оптимального плана
3.4. Содержание отчета по работе
Отчет должен содержать следующие пункты:

• 
  задание на работу с конкретными исходными данными студента,
  
• 
  математическая модель транспортной задачи для конкретных данных студента,
  
• 
  «равномерный» план перевозок, суммарные затраты на перевозки,
  
• 
  план перевозок, полученный методом «северо-западного» угла, суммарные затраты на перевозки,
  
• 
  план перевозок, полученный методом минимальной стоимости, суммарные затраты на перевозки,
  
• 
  оптимальный план перевозок, суммарные затраты на перевозки,
  
• 
  граф перевозок, построенный для оптимального плана,
  
• 
  выводы по работе.