Транспортнотехнологический факультет

Название	Транспортнотехнологический факультет
Дата	25.02.2019
Размер	242.9 Kb.
Формат файла
Имя файла	Auditornaya_kontrolnaya_rabota.docx
Тип	Задача #68813

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Сыктывкарский лесной институт (филиал)

федерального государственного бюджетного образовательного

учреждения высшего образования

«Санкт–Петербургский государственный

лесотехнический университет имени С.М.Кирова»

(СЛИ)

ТРАНСПОРТНО–ТЕХНОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

Кафедра «Физика и автоматизация технологических процессов и производств»

АУДИТОРНАЯ КОНТРОЛЬНАЯ РАБОТА
ВАРИАНТ №8

Выполнил:	__________________	Cтудент заочной формы обучения направления подготовки УТС, 3курс, группа АБ3330, Александров Владислав
проверил:	––––––––––––––––––		Преподаватель кафедры ФиАТПиП: Сундуков Е.Ю.

Сыктывкар 2017

Задача №2: Транспортная задача

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления. Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект

Задача: На трёх базах находится груз в количестве A1, A2, A3 условных единиц. Этот груз необходимо развести пяти покупателям, потребности которых составляют B1, B2, B3, B4, B5 условных единиц. Стоймости перевозок даны в матрице C. Задание: составить такой план перевозок, чтобы общая стоимость перевозок была минимальной.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов:

	B1	B2	B3	B4	B5	Запасы
A1	8	25	6	11	16	150
A2	4	14	12	15	17	230
A3	18	26	11	12	20	120
Потребности	160	90	80	70	100

Проверим необходимое и достаточное условие разрешимости задачи:
∑A = 150+ 230 + 120 = 500
∑B = 160 + 90 + 80 + 70 + 100 = 500

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
X_1,4+Х_1,5+Х_1,6+Х_1,7+Х_1,8≤150

X_2,4+Х_2,5+Х_2,6+Х_2,7+Х_2,8≤230

X_3,4+Х_3,5+Х_3,6+Х_3,7+Х_3,8≤120

X_1,4+Х_2,4+Х_3,4=160

X_1,5+Х_2,5+Х_3,5=90

X_1,6+Х_2,6+Х_3,6=80

X_1,7+Х_2,7+Х_3,7=70

X_1,8+Х_2,8+Х_3,8=100

Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).

Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

Далее введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.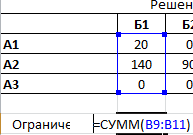

$c:\users\pc\appdata\local\microsoft\windows\inetcache\content.word\снимок23213123.png$

Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

$c:\users\pc\appdata\local\microsoft\windows\inetcache\content.word\снимок1231211.png$

Вносим известные значения потребности в товаре и объема производства.

Вводим формулу целевой функции СУММПРОИЗВ(B3:F5; B9:F11), где первый массив (B3:F5) – стоимость единицы перевозки товаров. Второй (B9:F11) – искомые значения транспортных расходов.

Вызываем команду «Поиск решения» на закладке «Данные». Заполняем диалоговое окно. В графе «Установить целевую ячейку» - ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» - массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.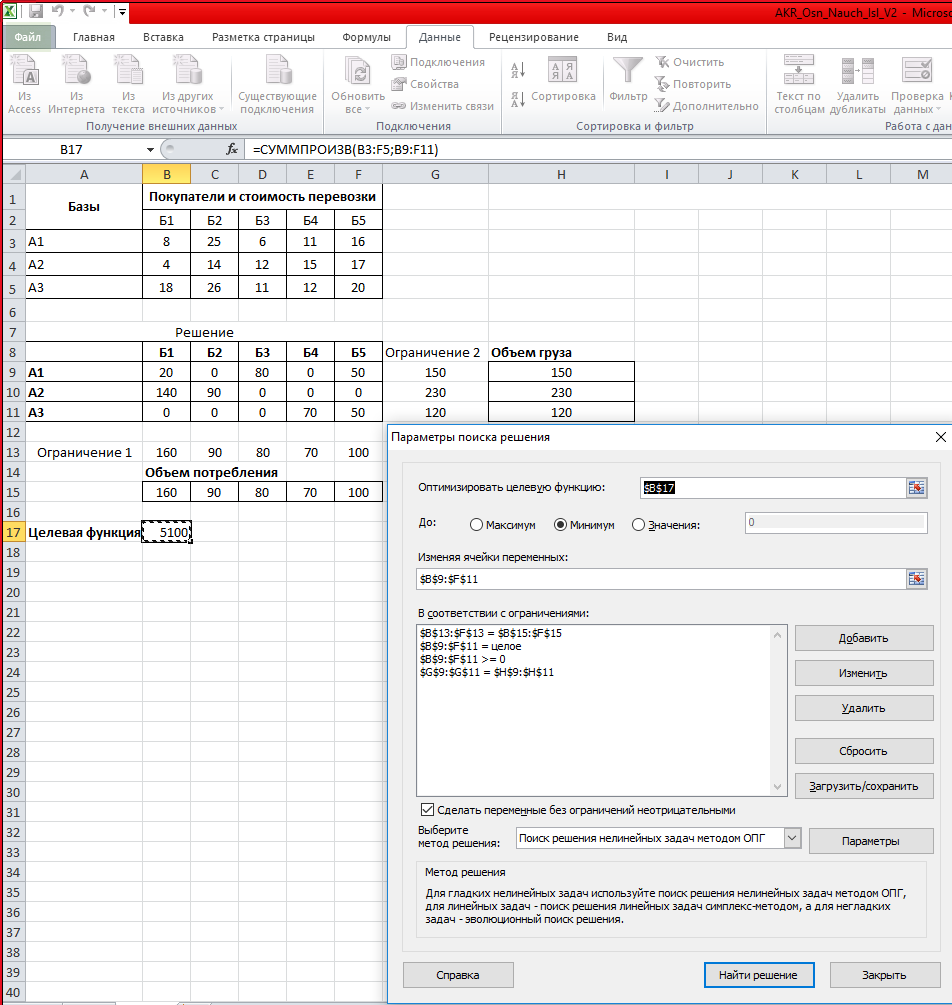

$c:\users\pc\appdata\local\microsoft\windows\inetcache\content.word\снимок21123222.png$

Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Базы	Покупатели и стоимость перевозки
Базы	Б1	Б2	Б3	Б4	Б5
А1	8	25	6	11	16
А2	4	14	12	15	17
А3	18	26	11	12	20

Решение							Объем груза
	Б1	Б2	Б3	Б4	Б5	Ограничение 2	150
А1	20	0	80	0	50	150	230
А2	140	90	0	0	0	230	120
А3	0	0	0	70	50	120

Ограничение 1	160	90	80	70	100
	Объем потребления
	160	90	80	70	100

Целевая функция	5100

Значение целевой функции для этого опорного плана равно 5100.

Задача №1:

Приведены показатели работы организаций некоторого региона по виду деятельности «Обработка древесины и производство изделий из дерева, кроме производства мебели», в частности, объем отгруженных товаров (млн. руб.):

А1	А2	А3	B1	B2	B3	B4	B5	C
150	230	120	160	90	80	70	100	8	25	6	11	16
								4	14	12	15	17
								18	26	11	12	20

Забиваем все данные по столбцам в Microsoft Excel. Далее находим функцию =ПРЕДСКАЗ. В этой функции необходимо ввести три значения:

Значение х. Заданный числовой аргумент, для которого необходимо предсказать значение y.
Диапазон значений y. Известные числа, на основании которых будет проводиться вычисление.
Диапазон значений x. Известные числа, на основании которых будет проводиться вычисление.

В свободную ячейку С10 введем формулу: =ПРЕДСКАЗ(А10;В2:В9;А2:А9). Функция находит значение y для заданного значения. Результат равен 29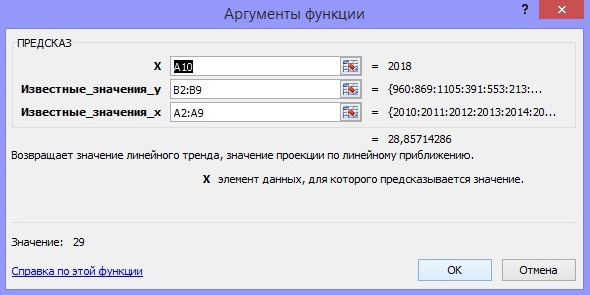

безымянный1.jpg

Далее выбираем «Формат ячеек», формат «Числовой», число десятичных знаков после запятой: 0.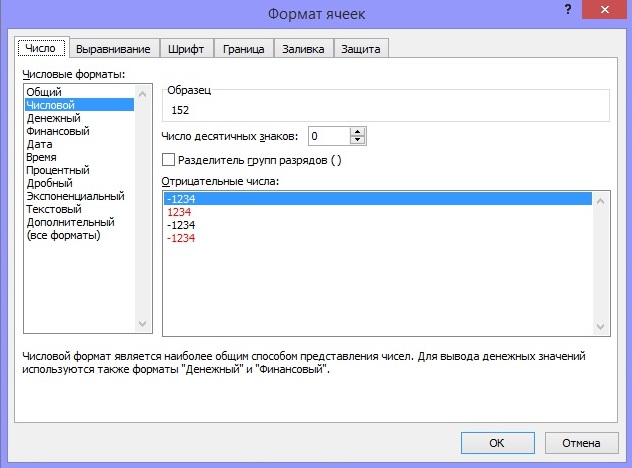

безымянный3.jpg

Затем построим график по имеющимся данным.Выделяем ячейка А2;В10, заходим в меню «Вставка» и выбираем «График». Далее выбираем значения осей «х» и «у» и Выделим график. Щелкнем правой кнопкой мыши – «Добавить линию тренда». В появившемся окне установим галочки напротив пунктов «Показывать уравнение» и «Поместить величину достоверности аппроксимации». Линия тренда призвана показывать тенденцию изменения данных.