|
|
Документ Microsoft Word. Туынды кмегімен функцияны зерттеу Функцияны суі мен кемуі
Туынды көмегімен функцияны зерттеу
1. Функцияның өсуі мен кемуі
Туындының қосымшаларының бірі оның функцияны зерттеуді, оның графигін салуда қолдану болып табылады. Функцияның өсуі мен кемуінің қажетті және жеткілікті шарттарын тұжырымдайық.
Теорема 1. (қажетті шарт). Егер 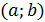 интервалында дифференциалданатын интервалында дифференциалданатын 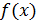 функциясы өсетін (кемитін) болса, онда функциясы өсетін (кемитін) болса, онда  үшін үшін  ( (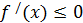 ). ).
Д/уі. 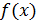 функциясы функциясы 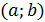 интервалында өсетін болсын. интервалында өсетін болсын. 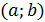 интервалынан х және интервалынан х және  кез-келген нүктелерін алайық және кез-келген нүктелерін алайық және  қатынасын қарастырайық. қатынасын қарастырайық. 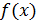 функциясы өседі, сондықтан да функциясы өседі, сондықтан да 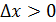 болса, онда болса, онда 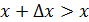 және және 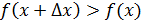 ; егер ; егер  болса, онда болса, онда 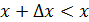 және және 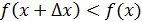 . Екі жағдайда да, . Екі жағдайда да, 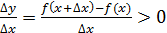 , себебі бөлшектің алымы мен бөлімі бірдей таңбалы. Теорема шарты бойынша , себебі бөлшектің алымы мен бөлімі бірдей таңбалы. Теорема шарты бойынша 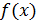 функциясының х нүктесінде туындысы бар және қарастырылатын, қатынастың шегі болып табылады. Сәйкесінше, функциясының х нүктесінде туындысы бар және қарастырылатын, қатынастың шегі болып табылады. Сәйкесінше,  . .  функциясы функциясы 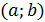 интервалында кемитін жағдайда осылай қарастырылады. интервалында кемитін жағдайда осылай қарастырылады.
Теорема 2. (жеткілікті шарт). Егер 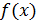 функциясы функциясы 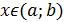 үшін үшін 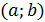 интервалында дифференциалданса және интервалында дифференциалданса және 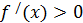 ( (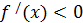 ) болса, онда осы функция (a; b) интервалында өседі (кемиді). ) болса, онда осы функция (a; b) интервалында өседі (кемиді).
Д/уі. 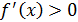 болсын. болсын. 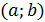 интервалында интервалында 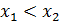 болатындай болатындай  және және 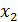 нүктелерін алайық. нүктелерін алайық. 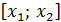 кесіндісінде Лагранж теоремасы қолданылады: кесіндісінде Лагранж теоремасы қолданылады:  , мұндағы , мұндағы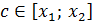 . Шарт бойынша, . Шарт бойынша,  , ,  . Сәйкесінше, . Сәйкесінше,  немесе немесе  , яғни , яғни 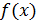 функциясы функциясы 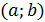 интервалында өседі. интервалында өседі.
Өспелі және кемімелі функциялар монотонды функциялар деп аталады.
2. Функцияның максимумы мен минимумы
Егер 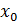 нүктесінің нүктесінің 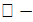 маңайы бар болып, осы маңайдың барлық маңайы бар болып, осы маңайдың барлық  x0 үшін x0 үшін 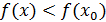 теңсіздігі орындалса, теңсіздігі орындалса, 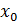 нүктесі нүктесі 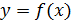 функциясының максимум нүктесі деп аталады. Функцияның минимум нүктесі де осылай анықталады: егер функциясының максимум нүктесі деп аталады. Функцияның минимум нүктесі де осылай анықталады: егер
|
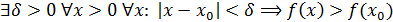
|
(9.1)
|
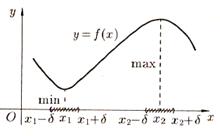
болса, 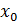 функциясының минимум нүктесі. 9.1-суретте функциясының минимум нүктесі. 9.1-суретте  -минимум нүктесі, -минимум нүктесі, 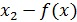 -функциясының максимум нүктесі -функциясының максимум нүктесі
|
|
|
|
9.1–сурет– -min нүктесі, -min нүктесі, 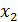 - функциясының max нүктесі - функциясының max нүктесі
|
|
Максимум (минимум) нүктедегі функция мәні функцияның максимум (минимумы) деп аталады. Функцияның максимумы (минимумы) функцияның экстремумы деп аталады.
Теорема 3. (экстремумның қажетті шарты). Егер 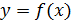 дифференциалданатын функциясының дифференциалданатын функциясының 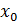 нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең: f /(x0)=0. нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең: f /(x0)=0.
Д/уі. 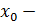 максимум нүкте болсын делік. Яғни, максимум нүкте болсын делік. Яғни, 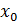 нүктесінің маңайында нүктесінің маңайында  теңсіздігі орындалады. Олай болса, теңсіздігі орындалады. Олай болса, 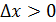 болғанда болғанда 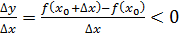 , ал , ал  болғанда, болғанда, 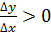 . Теорема шарты бойынша . Теорема шарты бойынша 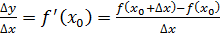 туындысы бар болады. туындысы бар болады. 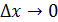 болғанда шекке көшу арқылы болғанда шекке көшу арқылы 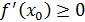 аламыз, егер аламыз, егер  және және  , егер , егер 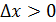 болса. Сондықтан, болса. Сондықтан, 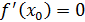 . Егер . Егер 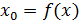 функциясының минимум нүктесі болса, 3- теоремасының тұжырымдамасы осылай дәлелденеді. функциясының минимум нүктесі болса, 3- теоремасының тұжырымдамасы осылай дәлелденеді.
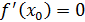 теңдігінің геометриялық мағынасы теңдігінің геометриялық мағынасы  дифференциалданатын функциясының экстремум нүктесінде, оның графигіне жүргізілген жанама Ox осіне параллель. дифференциалданатын функциясының экстремум нүктесінде, оның графигіне жүргізілген жанама Ox осіне параллель.
Үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді деп атайды.
Теорема 4. (экстремумның жеткілікті шарты). Егер  функциясы функциясы  күдікті нүктесінің қандай да күдікті нүктесінің қандай да  маңайында дифференциалданатын болса, және одан өткенде (солдан оңға) f /(x0) туындысы плюстен минусқа ауысса, маңайында дифференциалданатын болса, және одан өткенде (солдан оңға) f /(x0) туындысы плюстен минусқа ауысса, 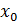 - максимум нүкте, минустан плюске - максимум нүкте, минустан плюске 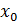 -минимум нүктесі -минимум нүктесі
Д/уі.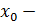 нүктесінің нүктесінің 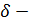 маңайын қарастырайық. маңайын қарастырайық.   және және  , ,  шарттары орындалсын делік. Сонда шарттары орындалсын делік. Сонда 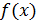 функциясы функциясы 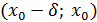 интервалында өседі, ал интервалында өседі, ал 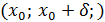 интервалында кемиді. Бұдан, интервалында кемиді. Бұдан, 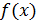 функциясының функциясының 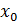 нүктесіндегі мәні нүктесіндегі мәні 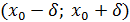 интервалындағы ең үлкен болатындығы шығады, яғни барлық интервалындағы ең үлкен болатындығы шығады, яғни барлық 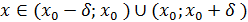 үшін үшін 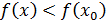 болады. Бұл болады. Бұл 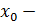 функциясының максимум нүктесі болатындығын білдіреді. функциясының максимум нүктесі болатындығын білдіреді.
|

|
|
|
9.2-сурет-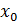 нүктесі max және min нүктелері нүктесі max және min нүктелері
|
|
Функцияны экстремумға зерттеу оның барлық экстремумдарын табу деген сөз. Функцияны экстремумға зерттеудің келесі ережелері шығады:
1) 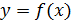 функциясының күдікті нүктелерін табу; функциясының күдікті нүктелерін табу;
2) олардың ішінен тек анықталу облысының кіретін ішкі нүктелерді таңдап алу;
3) таңдалған әрбір күдікті нүктелердің әрқайсысының оң жағынан және сол жағынан f /(x) туындысының таңбасын зерттеу;
4) 4. теоремасына (экстремумның жеткілікті шарты) сәйкес экстремум нүктелерді (егер олар бар болса) жазып алу және олардағы функция мәнін есептеу.
Теорема 5. Егер 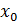 нүктесінде нүктесінде 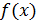 функциясының бірінші туындысы нөлге тең (f /(x0)=0)), ал функциясының бірінші туындысы нөлге тең (f /(x0)=0)), ал 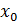 нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса, онда f //(x0)<0 болғанда нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса, онда f //(x0)<0 болғанда 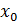 нүктесінде функция максимумға ие, ал f //(x0)>0 болғанда минимумға ие нүктесінде функция максимумға ие, ал f //(x0)>0 болғанда минимумға ие
Д/уі.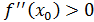 болсын делік. болсын делік. 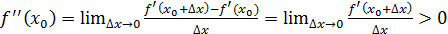 болғандықтан, болғандықтан, 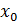 нүктесінің аз маңайында нүктесінің аз маңайында 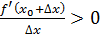 болады. Егер болады. Егер  болса, онда болса, онда 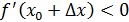 ; егер ; егер 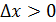 болса, онда болса, онда 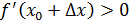 болады. Осылайша, болады. Осылайша, 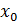 нүктесі арқылы өткенде бірінші туындының таңбасы минустан плюске өзгереді. Сәйкесінше, нүктесі арқылы өткенде бірінші туындының таңбасы минустан плюске өзгереді. Сәйкесінше, 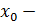 минимум нүкте. Егер минимум нүкте. Егер  болса, онда болса, онда 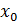 нүктесінде функция максимумға ие болатындығы осылайша дәлелденеді. нүктесінде функция максимумға ие болатындығы осылайша дәлелденеді.
3. Функцияның кесіндідегі ең үлкен және ең кіші мәні
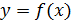 функциясы функциясы 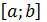 кесіндісінде үзіліссіз болсын. Мұндай функция өзінің ең үлкен және ең кіші мәнін қабылдайды және олар не кесіндісінде үзіліссіз болсын. Мұндай функция өзінің ең үлкен және ең кіші мәнін қабылдайды және олар не 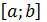 кесіндісінің ішкі нүктесінде, не кесіндінің ұштарында, яғни кесіндісінің ішкі нүктесінде, не кесіндінің ұштарында, яғни 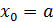 не не 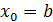 болғанда. Егер болғанда. Егер  болса, онда болса, онда 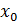 нүктесін берілген функцияның күдікті нүктелерінен іздек керек. нүктесін берілген функцияның күдікті нүктелерінен іздек керек.
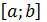 кесіндісінде функцияның ең үлкен, ең кіші мәндерін табудың келесі ережесін аламыз: кесіндісінде функцияның ең үлкен, ең кіші мәндерін табудың келесі ережесін аламыз:
1)  -да функцияның ең үлкен, ең кіші мәндерін табудың келесі ережелерін аламыз; -да функцияның ең үлкен, ең кіші мәндерін табудың келесі ережелерін аламыз;
2) табылған күдікті нүктелердегі функцияның мәнін есептеу;
3) кесінді ұштарында, яғни 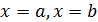 нүктелеріндегі функция мәнін есептеу; нүктелеріндегі функция мәнін есептеу;
4) барлық табылған мәндер ішінен ең үлкені мен ең кішісін таңдау.
4 .Функция графигінің дөңестігі, иілу нүктелері
Егер 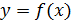 дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады. дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады.
Үзіліссіз 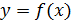 функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте–иілу нүктесі деп аталады. 9.3–суретте функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте–иілу нүктесі деп аталады. 9.3–суретте 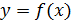 қисығы қисығы 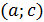 интервалында жоғарыдан ойыс, интервалында жоғарыдан ойыс, 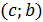 интервалында төменнен ойыс, ал интервалында төменнен ойыс, ал 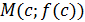 –иілу нүктесі. –иілу нүктесі.
|

|
|
|
9.3-сурет. М нүктесі иілу нүктесі
|
|
Жоғарыдан және төменнен ойыс интервалдар келесі теореманың көмегімен табылады.
Теорема 5. Егер 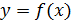 функциясының функциясының 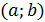 интервалының барлық нүктесінде екінші туындысы теріс, яғни f //(x)<0 болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер f //(x)>0, интервалының барлық нүктесінде екінші туындысы теріс, яғни f //(x)<0 болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер f //(x)>0, 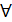 x x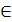 (a; b) болса, функция графигі төменнен дөңес. (a; b) болса, функция графигі төменнен дөңес.
Д/уі: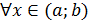 үшін үшін  болсын. Функция графигінен абциссасы: болсын. Функция графигінен абциссасы: 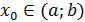 болатын кез-келген нүктені алып, М арқылы жанама жүргізейік. Функция графигі жанамадан төмен орналасқанын көрсетейік. Ол үшін болатын кез-келген нүктені алып, М арқылы жанама жүргізейік. Функция графигі жанамадан төмен орналасқанын көрсетейік. Ол үшін 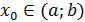 нүктесінде нүктесінде 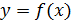 қисығының қисығының  ординатасымен ординатасымен  салыстырайық. Біз білетіндей, жанаманың теңдеуі мына түрде болады: салыстырайық. Біз білетіндей, жанаманың теңдеуі мына түрде болады:
 , яғни , яғни 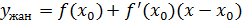 . Лагранж теоремасы бойынша . Лагранж теоремасы бойынша 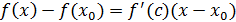 , мұнда c , мұнда c 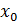 және және 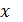 нүктелерінің арасында жатыр. Сондықтан, нүктелерінің арасында жатыр. Сондықтан,
|
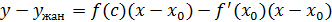 , ,
|
|
яғни 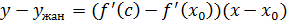 . .  айырманы тағы да Лагранж формуласы бойынша түрлендірелік: айырманы тағы да Лагранж формуласы бойынша түрлендірелік:
мұнда 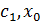 және с арасында жатыр. және с арасында жатыр.
Осылайша,
|
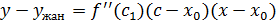 . .
|
|
Осы теңдікті зерттейміз:
1) егер  , онда , онда 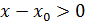 , ,  және және . Демек . Демек  , яғни , яғни ; ;
2) егер 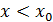 , онда , онда 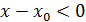 , , 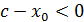 және және . Демек . Демек  , яғни , яғни . .
Сонымен, 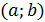 интервалының барлық нүктелерінде жанаманың ординатасы графиктің ординатасынан үлкен екендігі дәлелденді, яғни функция графигі жоғарыға дөңес. Осыған ұқсас, интервалының барлық нүктелерінде жанаманың ординатасы графиктің ординатасынан үлкен екендігі дәлелденді, яғни функция графигі жоғарыға дөңес. Осыған ұқсас, 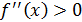 болғанда графиктің төменге дөңестігі дәлелденеді. Функцияның графигінің иілу нүктелерін табу үшін келесі теорема қолданылады. болғанда графиктің төменге дөңестігі дәлелденеді. Функцияның графигінің иілу нүктелерін табу үшін келесі теорема қолданылады.
Теорема 6. (иілу нүктелерінің бар болуының жеткілікті шарты). Егер 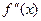 екінші ретті туынды x0 нүктесі арқылы өткен де, таңбасын өзгертсе, онда графиктің абсцисссасы екінші ретті туынды x0 нүктесі арқылы өткен де, таңбасын өзгертсе, онда графиктің абсцисссасы 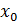 болатын графиктің нүктесі иілу нүктесі болады. болатын графиктің нүктесі иілу нүктесі болады.
5 .Функция графигінің асимптотасы
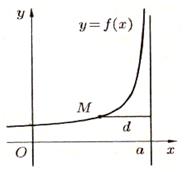
Егер функцияның асимптоталарына білсек, онда оның графигін салу жеңіл болады. Асимптота ұғымы гиперболаның формуларын зертегенде қарастырылған. Еске түсіріп өтелік. Қисықтың асимптотасы деп координатаның бас нүктесінен бастап қисық бойынан әртүрлі жолмен бөліп алғандағы нүктеден түзуге дейінгі арақашықтық нөльге ұмтылатын, түзуді айтамыз (9.3-суретті қара). Асимптоталар тік, көлденең, көлбеу болады.
|
|
|
|
9.4-сурет. х=а түзуі y=f(x) функциясының асимптотасы
|
|
 түзуі түзуі 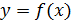 функциясының графигінің тік асимптотасы деп аталады, егер функциясының графигінің тік асимптотасы деп аталады, егер 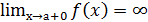 немесе немесе 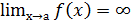 немесе немесе 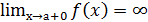 . .
6. Функцияны зерттеудің жалпы схемасы және графигін салу
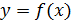 функциясын зерттеуді белгілі тізбек бойынша жүргізу қажет. функциясын зерттеуді белгілі тізбек бойынша жүргізу қажет.
1. Функцияның анықталу облысын табу;
2. Графиктің координаталар осімен қиылысу нүктелерін табу (мүмкін болса);
3. Функцияның таңбасы тұрақты интервалдарын табу (f(x)>0 немесе f(x)<0 болатындай аралықтарды табу);
4. Функцияның жұп, тақ, не жалпы түрдегі болатындығын анықтау;
5. Функция графигінің асимптоталарын табу;
6. Функцияның монотондық интервалдарын табу;
7. Функцияның экстремумдарын табу;
8. Функция графигінің ойыс интервалдары мен иілу нүктелерін табу;
Жүргізілген зерттеу негізінде функция графигін салу қарапайым функциялар үшін 1, 2, 7 операцияларды орындау жеткілікті. Егер барлық 8 операцияны орындаған соң да функция графигі аса түсінікті болмаса, онда функцияны периодтылыққа зерттеп, қосымша бірнеше нүктелерді салып функцияның басқа қасиеттерін зерттеу керек. Кейде зерттеу жүргізе отырып, функция графигін салу тиімді. |
|
|
 Скачать 135.35 Kb.
Скачать 135.35 Kb.



