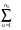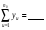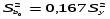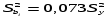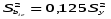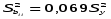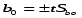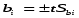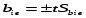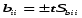Лаб. раб. №3 по ОНИС Применение полного факторного эксперимента.. Тверской государственный технический университет (Твгту) Кафедра Строительные и дорожные машины и оборудование

• Название: Тверской государственный технический университет (Твгту) Кафедра Строительные и дорожные машины и оборудование
• Дата: 17.02.2019
• Размер: 0.67 Mb.
• Имя файла: Лаб. раб. №3 по ОНИС Применение полного факторного эксперимента..docx
• Тип: Методические указания; #67849
• страница: 3 из 4

Кинематические схемы стенда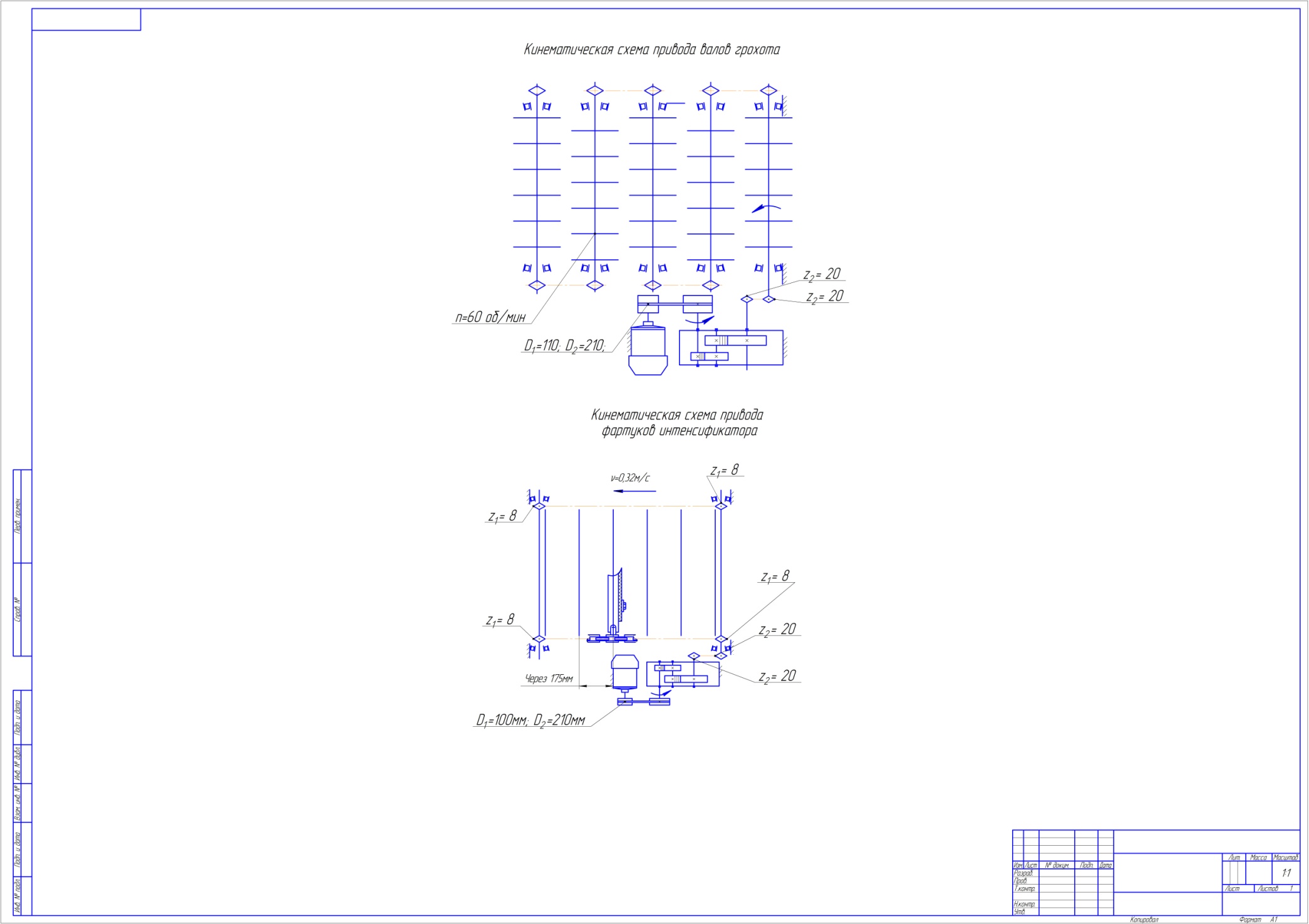

Рис. 2. Кинематические схемы стенда

3. Установка угла рабочей поверхности

С помощью стойки, на которой приварены уголки, соответствующие углам рабочей поверхности: 5, 10, 15 градусов. Стенд вывешивается домкратом на нужный угол. Затем устанавливается подставка. Промежуточные углы можно регулировать виброопорой.

Виброопора состоит:

1. 
   Подставка;
   
2. 
   Резиновая прокладка;
   
3. 
   Регулировочный болт;
   
4. 
   Гайки М16(нижняя – высота; верхняя – фиксация положения).
   

Установка угла:

1. 
   Расслабить верхнюю контргайку;
   
2. 
   Открутить нижнюю гайку;
   
3. 
   Откручивать – опускать;
   
4. 
   Закручивать – поднимать;
   
5. 
   Затянуть верхнюю контргайку.
   

3. 
   Теоретическая часть
   

Факты - это воздух ученого. И. П. Павлов

По числу варьируемых факторов эксперименты классифицируются на (однофакторный и многофакторный).

Однофакторным называют такой эксперимент, когда изучается воздействие на объект исследования только одного управляемого переменного фактора.

Многофакторным называется эксперимент, при котором на исследуемый объект одновременно действует несколько управляющих (переменных) факторов.

Схема эксперимента

Z₁ Z₂ Z₃ Z_m Z₁ Z₂ Z₃ Z_m

…

X₁ Y₁

X Y X₂ Y₂

X₃ Y₃

X_n Y_m

… …
W₁ W₂ W₃ W_p W₁ W₂ W₃ W_p

а) однофакторного, б) многофакторного.

Рис. 3. Схема «черною ящика». Хn, Zm, Wp -соответственно: управляющие, контролируемые и возмущающие (неконтролируемые), воздействующие на объект исследования; у - выходной: параметр (результат эксперимента)

В подавляющем большинстве случаев эксперименты многофакторные. При их проведения принимается либо классический, либо факторный план.

Классический многофакторный эксперимент представляет собой последовательность однофакторных экспериментов, при которых все независимые переменные, кроме одной, принимаются постоянными. В таких экспериментах нельзя определить характер взаимодействия факторов между собой и их совместное влияние на выходной параметр.

Полный факторный эксперимент (ПФЭ) – это эксперимент, в котором осуществляется перебор всех возможных сочетаний уровней факторов.

Фиксированный набор уровней факторов определяет одно из возможных состояний системы («черного ящика»). Одновременно это есть условия проведения одного из возможных опытов.

Если перебрать все возможные сочетания уровней факторов х_nсистемы, то получим множество состояний системы. Каждому состоянию соответствует какое-то значение параметра оптимизации Y_m.

Основы многофакторного эксперимента по факторному плану были заложены в конце 20-х годов XX века. Многофакторное планирование, основанное на достаточно общем математическом аппарате, позволяет:

- получить математическую модель процесса, которую можно использовать, в частности, при управлении;

- вскрыть объективные закономерности и получить дополнительную информацию о процессе;

- проверить адекватность представления результатов эксперимента определенной интерполяционной зависимостью.

Метод однофакторного эксперимента широко распространен. Однако, при исследовании сложных процессов, особенно с задачей их оптимизации, все большее применение находит метод многофакторного эксперимента.

Переменные x₁, x₂, x₃,… x_n принято называть факторами.

Выходные величины Y₁, Y₂ , Y₃ … Y_m также могут быть разнородными: измеряемыми и не измеряемыми.

1. 
   Планирование эксперимента
   

Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для получения математической модели процесса [1].

При этом важно учитывать следующее: стремление к минимизации числа опытов; одновременное варьирование всех переменных, определяющих процесс; выбор четкой стратегии.

Планирование эксперимента резко повышает точность и уменьшает объем, экспериментальных исследований. Оно позволяет находить оптимум функции, характеризующей исследуемый процесс.

Модель процесса описывается уравнением регрессии, коэффициенты которого определяются при помощи специальных методов (например, методом наименьших квадратов).

В зависимости от условий решаемой задачи выходная величина называется: откликом, функцией цели, функцией отклика, параметром оптимизации.

Обычно аналитическая связь между входом и выходом неизвестна, а известны факторы x_i, и подлежащие исследованию выходные величины Y_i.

В этом случае задачами планирования эксперимента могут быть:

1. Раскрытие механизма явления, т. е. нахождение такого аналитического выражения которое в области возможных значений факторов х_iдостаточно точно совпадает с неизвестной зависимостью.
Y = f(x₁, x₂, x₃,… x_i)(3.1)

Эксперименты по раскрытию механизма явления называются иногда интерполяционными или регрессионными.

Область возможных или допустимых значений факторов х_iназывается областью определения.

2. Определение экстремума (максимума или минимума) отклика в области определения. Такие эксперименты называются экстремальными.

3. Выбор подходящей модели для описания объекта или определение параметров известной функциональной зависимости.

3.2. Выбор факторов

Приступая к планированию эксперимента, необходимо выбрать факторы и определить:

- влияние их на выходную величину Yкакими из них можно задаваться по желанию экспериментатора и какие неуправляемы или случайны;

- точность аппаратуры, с помощью которой задаются значения варьируемых факторов и измеряются значения выхода Y;

- являются ли факторы независимыми или зависимыми величинами.

Выбранные факторы должны быть доступны измерению с точностью примерно на порядок большей, чем измерение выходной величины.

Необходимо выбрать для каждого эксперимента интервал варьирования факторов, которым называется половина разности между большим (верхним) и меньшим (нижним) значением фактора (x_1н, х_1в, х_2н, х_2в).

Значение фактора в центре области эксперимента называется его основным уровнем и отмечается подстрочным индексом «О» (х₁₀, х₂₀, ...).

3. 
   Построение планов полного факторного эксперимента
   

Полный факторный эксперимент состоит из следующих частей: сбор и анализ априорной информации; выбор входных и выходных переменных, области экспериментирования; выбор математической модели, с помощью которой будут представляться экспериментальные данные; выбор критерия оптимальности и плана эксперимента; определение метода анализа данных; проведение эксперимента; проверка статистических предпосылок для полученных экспериментальных данных; обработка результатов; интерпретации и рекомендаций.

Полным факторным называется такой эксперимент, в котором реализуются все возможные комбинации (наборы), уровней факторов. Если kфакторов варьируется на двух уровнях, то число всех возможных наборов - N₂= 2^k.

Если kфакторов варьируется на трех уровнях, то N₃= 3^k. В полном факторном эксперименте число опытов равно числу различных наборов, т. е. различных точек факторного пространства. С увеличением числа факторов kбыстро растет число опытов.

Двухфакторный эксперимент. Представляем план эксперимента в виде таблицы-матрицы (табл. 3.3.1). Матрица содержит четыре (2²) строки и два основных столбца переменных х₁и х₂. В летальных столбцах записываются измерения отклика Yв отдельных точках факторного пространства.

Матрица двухфакторного эксперимента

Таблица 3.3.1

№ опыта	Уровни переменных		Отклики
	Х1	Х2	Yu1	Yu2	Yuj
1 2 3 4	-1 -1 +1 +1	-1 +1 -1 +1	Y11 Y21 Y31 Y41	Y12 Y22 Y32 Y42	Y1j Y2j Y3j Y4j

В каждой точке может проводиться несколько опытов п_и, которые называют параллельными.

Для проведения эксперимента значения факторов разделяются на уровни, задаваемые соответствующими строками. После этого измеряются значения отклика. Если проводится одна серия опытов, то заполняется одна графа: у₁₁, у₂₁, у₃₁ ,у₄₁.

При низкой точности измерений отклика или. при действии случайных факторов повторяется и записывается еще одна серия результатов: у₁₂, у₂₂, у₃₂, у₄₂.

Для повышения точности серии измерений могут повторяться несколько раз (параллельные опыты).

Трехфакторный эксперимент. Для построения плана полного факторного, эксперимента 2³ необходимо составить всевозможные комбинации из трех факторов (таблица 3.3.2.), когда каждый варьируется на двух уровнях (+1 и -1).

Планирование эксперимента позволяет варьировать ряд факторов и получать одновременно количественные оценки всех проявляющихся эффектов. При этом, в отличие от классического регрессионного анализа, избежать корреляции между коэффициентами уравнения регрессии.

Матрица трехфакторного эксперимента.

Таблица 3.3.2

№ опыта	Уровни переменных
	Х1	Х2	Х3
1 2 3 4 5 6 7 8	- - - - + + + +	- - + + - - + +	- + - + - + - +

Совокупность наборов даёт матрицу планирования полного факторного эксперимента (ПФЭ) 2³, в которой жирными линиями выделена матрица ПФЭ 2², а отдельные уровни факторов обозначаются символами + (плюс) и - (минус).

Отсюда следует правило получения матрицы ПФЭ 2³, в которой матрица ПФЭ 2² повторяется дважды: первый раз при Х₃ = -1, второй - при Х₃ = +1, что соответствует нижней и верхней граням куба.

При проведении опытов в данной последовательности не учитываемые медленно меняющиеся величины могут исказить результаты. Поэтому при нестабильных условиях эксперимента последовательность опытов должна быть случайной.

Модель процесса. Выбор модели (уравнение модели) в методе планирования эксперимента - неформализованный этап, который основывается обычно на интуитивных соображениях с учетом предыдущего опыта экспериментатора, а количественное определение коэффициентов выбранных уравнений модели - на результатах эксперимента. Поэтому правильный выбор модели должен подтверждаться экспериментально.

Модель определяется переменными x_i и постоянными параметрами b_i и в общем случае имеет вид:

y = Y (x₁, x₂, … x_k, b₁, b₂, …,b_m) (3.2)

В планировании эксперимента чаще всего применяются модели линейные относительно переменных x_i и параметров b_i ;

y = b₀+b₁x₁+b₂x₂+b₃x₃+…+b_kx_k (3.3)

Однако модели могут быть не только линейными, но и нелинейными, по результатам опытов, выполненных в соответствии с принятым планом эксперимента, можно оценить коэффициенты уравнении регрессии вида:

Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₁x₁²+b₂₂x₂²+b₃₃x₃² (3.4)

В этом уравнении факторы представлены в кодированном виде, для получения экспериментально – статистической модели необходимо определять все коэффициенты, входящие в уравнение 3.2, а также дисперсию воспроизводимости в центре плана и дисперсии коэффициентов уравнения.

Определение коэффициентов модели. Уравнение модели 3.4 содержит неизвестные коэффициенты b_i .

Если эти коэффициенты определяются по статистическим данным, то получаются не точные их значения, а статистические оценки, которые в математической статистике обозначаются малыми латинскими буквами (а, b, с...), в отличие от точных значений, обозначаемых малыми греческими буквами (α, β, µ...). Из-за случайности величин Y получаем не точное уравнение модели, а его оценку.

Уравнение (3.2) называется моделью или уравнением регрессии, а функция у(х₁, ..., х_n) - поверхностью или (при- i > 2) гиперповерхностью регрессии.

Метод наименьших квадратов (МНК). Для отыскания оценок bi применяется метод наименьших квадратов, а сама процедура отыскания называется регрессионным анализом.

В задачах регрессионного анализа принимается обычно следующее принципиальное допущение:

- все независимые переменные факторы x_l, x₂ , ..., х_k задаются абсолютно точно и являются неслучайными величинами;

- предполагается, что случайная величина у_u распределена по нормальному закону, а ее дисперсии в отдельных точках факторного пространства - однородны.

4. Последовательность проведения работы

1. 
   Подготовить экспериментальные данные и получить допуск у преподавателя.
   
2. 
   Определить область планирования эксперимента, число действующих факторов, функцию отклика.
   
3. 
   Провести проверку экспериментальных данных на однородность и нормальность.
   
4. 
   Запустить программу «полный факторный эксперимент».
   
5. 
   Провести расчет матрицы планирования полнофакторного эксперимента, занести матрицу в протокол (необходимо обратить внимание, что матрица заполняется в строгом соответствии с планом эксперимента).
   
6. 
   Получить уравнение регрессии. Занести результаты в протокол.
   
7. 
   Провести сравнение экспериментальных и расчетных значений. Занести в протокол полученную таблицу.
   
8. 
   Провести оценку значимости коэффициентов регрессии и оценку адекватности полученного уравнения. Результаты занести в протокол.
   
9. 
   Рассчитать значения выходного параметра. Занести результаты в протокол.
   
10. 
    Рассчитать отклонение расчетного значения выходного параметра от экспериментальных данных в центре плана.
    
11. 
    Написать выводы о проделанной работе.
    
12. 
    Подготовиться к отчету лабораторной работы преподавателю.
    

5. Выполнение лабораторной работы

Цель лабораторной работы - изучение способа построения имитационной модели сложной системы по результатам полного факторного эксперимента. Анализ точности полученных моделей.

Требуется:

1. 
   записать матрицу планирования ПФЭ типа 2³ с учетом перекрестных связей между факторами;
   
2. 
   установить влияние подачи, угла наклона, и фракции на мощность сепаратора (зависимость N = f (q, α, Ф).
   
3. 
   по результатам ПФЭ составить имитационную модель исследуемой системы Y=f(х₁, х₂, х₃);
   
4. 
   сделать выводы о степени точности полученных моделей.
   

Многофакторный эксперимент проводим по программе центрального композиционного ротатабельного планирования второго порядка.

Рототабельный центрально-композиционный план строится с использованием в качестве ядра плану ПФЭ 2ⁿ добавляются “звездные” точки - по две на каждый фактор и несколько точек в центре плана. “Звездные” точки должны располагаться на поверхности гиперсферы с радиусом R, на которой лежат и точки плана ПФЭ 2ⁿ.

Для удобства записи плана эксперимента и обработки экспериментальных данных обычно пользуются кодированными значениями факторов, которые обозначаются малыми буквами х₁ , х₂...

Из априорной информации и в ходе предварительных экспериментов были выявлены границы численных значений факторов.

Принятые в исследовании уровни и интервалы варьирования факторов для выполнения лабораторной работы необходимо взять из приложения №1 и заносить в таблицу 4.1.

Исходные данные для расчет

Таблица 4.1

Вариант №_____ Факторы	Обозна- чение	Интервал варьирования	Значение факторов
			+1,682	+1	0	-1	-1,682
q-подача смеси, (кг/с)	Х1
α- угол наклона, град.	Х2
Ф - фракция щебня, %	Х3

Для построения матрицы планирования трехфакторного эксперимента 2³ введем фиктивную переменную х₀= +1. По аналогии фиктивную переменную можно внести в любой план эксперимента.

Матрица планирования трехфакторного эксперимента 2³ и результаты опытов с учетом значений фиктивной переменной приведены в таблице 4.2. Где центральный композиционный ротатабельный план второго порядка для трех факторов состоит, из плана полного факторного эксперимента 2³ (опыты 1 - 8), шести опытов в «звездных точках» (опыты 9 - 14), и шести опытов в центре плана (опыты 15 - 20).
Матрица планирования трехфакторного эксперимента

и результаты опытов

Таблица 4.2

Номер опыта	Ф А К Т О Р Ы				Мощность, N(Y) кВт
	Х0	Х1	Х2	Х3
1	+1	+1	+1	+1	Y1
2	+1	+1	+1	-1	Y2
3	+1	+1	-1	+1	Y3
4	+1	+1	-1	-1	Y4
5	+1	-1	+1	+1	Y5
6	+1	-1	+1	-1	Y6
7	+1	-1	-1	+1	Y7
8	+1	-1	-1	-1	Y8
9	+1	+1,682	0	0	Y9
10	+1	-1,682	0	0	Y10
11	+1	0	+1,682	0	Y11
12	+1	0	-1,682	0	Y12
13	+1	0	0	+1,682	Y13
14	+1	0	0	-1,682	Y14
15	+1	0	0	0	Y15
16	+1	0	0	0	Y16
17	+1	0	0	0	Y17
18	+1	0	0	0	Y18
19	+1	0	0	0	Y19
20	+1	0	0	0	Y20

Иногда требуется так описать область факторного пространства, чтобы точность во всех направлениях поиска была одинаковая при равном расстоянии от центра планирования. Получение такого описания возможно на базе рототабельного центрального композиционного плана (РЦКП).

В отличие от ОЦКП этот тип планирования даже при k = 3 требует использования вычислительной техники для расчета коэффициентов полинома и проверки гипотез из-за сложных расчетных алгоритмов и больших временных затрат.

Свойство рототабельности, т.е. симметричности информационных контуров, достигается благодаря специальному планированию информационной матрицы, а именно выбору определенного значения «звездного» плеча и количества экспериментов в центре плана. Значения результатов опытов, который состоит из полного факторного эксперимента 2³ (опыты 1 - 8), - в «звездных точках» (опыты 9 - 14), - в центре плана (опыты 15 - 20) для выполнения лабораторной работы, зависят от числа факторов К = 3  приведены в табл. 4.2¹.
Матрица планирования трехфакторного эксперимента

и результаты опытов

Таблица 4.2¹

Номер опыта	Ф А К Т О Р Ы				Мощность, N(Y) кВт
	Х0	Х1	Х2	Х3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Таблица 4.3
Принимаемые формулы и значения расчетных величин коэффициентов уравнения регрессии при К = 3

№ п/п	Определяемая величина	Расчетная формула	Значение расчетных величин
1	Свободный план уравнения регрессии b0		________
2	Коэффициенты при линейных эффектах bi b1 b2 b3		________ ________ ________
3	Коэффициенты при эффектах взаимодействия bie b12 b13 b23		________ ________ ________
4	Коэффициенты при квадратических эффектах bii b11 b22 b33		________ ________ ________

При планировании эксперимента следует предусмотреть, чтобы определитель системы отличался от нуля. Тогда вычислительная процедура упрощается.

Основные достоинства планов ПФЭ - простота определения коэффициентов уравнения регрессии, возможность учета произведений взаимодействия факторов без изменения плана основного эксперимента. Преимущества любой матрицы ПФЭ достигаются за счет особого построения плана эксперимента, при котором матрица обладает свойствами ортогональности, нормировки, симметрии и рототабельности.

Свойство ортогональности: сумма построчных произведений элементов любых двух граф равна нулю.

Дисперсию воспроизводимости определяем по результатам опытов в центре плана. Для вычисления составим вспомогательную таблицу для расчета S_y².

Таблица 4.4

Номер опыта	yu		yu -	(yu – )2	Sy2
15 16 17 18 19 20	______ ______ ______ ______ ______ ______	= _________	_____ _____ _____ _____ _____ _____	______ ______ ______ ______ ______ _______	=_______________
				_______

Дисперсии, характеризующие ошибки в определении коэффициентов уравнения регрессии, вычисляют по формулам, указанным в

Применяем формулы и значения расчетных величин дисперсии при k=3.

Таблица 4.5

№	Определяемая величина	Расчетная формула	Значение расчетных величин
1	Дисперсия свободного числа уравнения регрессии Sbo2		________
2	Дисперсия коэффициентов при линейных эффектах Sbi2		________ ________ ________
3	Дисперсия коэффициентов при эффектах взаимодействия Sbie2		________
4	Дисперсия коэффициентов при квадратических эффектах Sbii2		________
5	Доверительные интервалы для коэффициентов ∆b0 ∆bi ∆bie ∆bii	∆ ∆ ∆ ∆	±_______ ±_______ ±_______ ±_______

Где t=2,57 – табличное значение критерия Стьюдента при 5% - ном уровне значимости и числе степеней свободы f = 5.

Коэффициенты b₃, b₁₂, b₁₃, b₂₃, b₃₃, меньше доверительных интервалов, поэтому их можно признать статистически незначимыми и исключить из уравнения регрессии. После преобразования выражение (3.4) примет вид:

Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₁x₁²+b₂₂x₂²+b₃₃x₃² (4.2)

После определения коэффициентов уравнения получим следующие значения: b₀ = ____; b₁ = ____; b₂ = ____; b₃ = ____; b₁₂ = ____; b₁₃ = ____; b₂₃ = ____; b₁₁ = ____; b₂₂ = ____; b₃₃= ____ .
В результате использования планирования второго порядка получим следующее уравнение регрессии:

Y=__+__x₁+__x₂+__x₃+__x₁x₂+__x₁x₃+__x₂x₃+__x₁²+__x₂²+__x₃² (4.3)

Проверку гипотезы адекватности модели производим по критерию Фишера. Для этого определяем дисперсию адекватности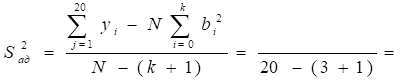


Поставив полученное значение в формулу для определения расчетного значения Fр – критерия Фишера получим: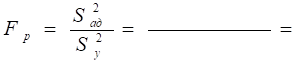

При 5% -ном уровне значимости и числе степеней свободы для числителя f₁ = ____ и знаменателя f₂ = ____ табличное значение Fт = _____.

Так как Fр < Fт, то модель, представленная уравнением адекватна.

Переходя от кодированных (Х₁, Х₂, Х₃) обозначении факторов к натуральным (q, α, Ф), получим зависимость мощности от рассмотренных параметров процесса сепарации:

Y = (4.4)

Уравнение (4.4) адекватно, поэтому его можно использовать как интерполяционную формулу для вычисления величины N.
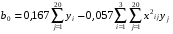
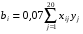
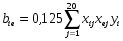
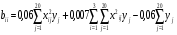
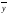
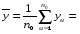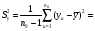