Творческий отчёт "Формирование математической грамотности. Новые подходы к содержанию математического образования в условиях реализации фгос ооо"
 Скачать 284.5 Kb. Скачать 284.5 Kb.
|
|
Творческий отчёт "Формирование математической грамотности. Новые подходы к содержанию математического образования в условиях реализации ФГОС ООО" Автор: Мартынова Ульяна Николаевна учитель математики МБОУ "Лицей имени С.Н. Булгакова" г. Ливны Орловской области Содержание: Стр. 1. Определение математической грамотности и её компоненты 3 2. Приёмы формирования математической грамотности 5 3. Поэтапное развитие различных умений, составляющих основу математической грамотности 8 4. Формирование финансовой грамотности 12 5. Приложения «Цель обучения ребенка состоит в том, чтобы сделать его способным развиваться дальше, без помощи учителя». Элберт Хаббард 1. Определение математической грамотности и её компоненты Математика является одним из самых важных достижений культуры и цивилизации. Без нее развитие технологий и познание природы были бы немыслимыми вещами! Эта точная наука крайне важна не только для человечества в целом, но для интеллектуального совершенствование конкретного индивида. Ведь математика позволяет развить важные умственные качества. Она организует наше мышление и дает опыт применения самых разных умственных приемов: от парадоксальных утверждений до моделирования. Математический язык способствует формированию устойчивой связи между словесным, изобразительным и знаковым способом передачи информации. Умение считывать информацию, поданную разными способами, приобретает особое значение в эпоху информатизации, и роль математического образования в развитии способности оперировать любой системой представления информации становиться ключевой. В Федеральном государственном образовательном стандарте обозначена необходимость и важность привести современное школьное образование в соответствие с потребностями времени, современного общества, которое отличается изменчивостью, многообразием существующих в нем связей, широким и неотъемлемым внедрением информационных технологий. Главным становится функциональная грамотность, так как это "способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний". Одним из ее видов является математическая грамотность. Словосочетание «математическая грамотность» появилось в контексте международного тестирования в 1991 г. В исследовании PISA "математическая грамотность - способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину". Компоненты математической грамотности: - воспроизведение математических фактов, методов и выполнение вычислений - установление связей и интеграции материала из разных математических тем, необходимых для решения поставленной задачи - математические размышления, требующие обобщения и интуиции Исследование PISA, в котором приоритетным направлением было исследование математической грамотности, показывают, что российские учащиеся имеют невысокие результаты. Результаты международного исследования PISA для России выглядят печально: 2000 год – из 31 страны Россия заняла – 27место; 2003 год – из 43 стран Россия заняла – 32 место; 2006 год – из 57 стран Россия заняла – 36 место; 2009 год – из 65 стран Россия заняла – 41 место. 2018 год — из 78 стран Россия заняла 27 место Это говорит о том, что наша система обучения не формирует у учащихся умения выходить за пределы учебных ситуаций, она лишь дает определенную базу знаний. Поэтому важнейшей задачей образования является усиление прикладной направленности школьного курса математики, то есть осуществление связи его содержания и методики обучения с практикой. Поэтому процесс обучения математике должен строиться не только из изучения основной программы курса, но и из овладения приложениями математики. Необходимо изменить приоритеты в школьном образовании, переориентироваться на компетентностный подход, непрерывное самообразование, овладение новыми информационными технологиями, умение сотрудничать и работать в группах и др. Прочное усвоение материала достигается посредством учебного процесса, в центре которого находится ученик, поэтому на протяжении всех уроков необходимо: • Создание той среды, которая позволяет личности чувствовать себя свободно и безопасно в процессе обучения. • Формирование саморегулирования, что обеспечивает самонаправленность, самостоятельное определение проблемы и цели, самостоятельный выбор стратегий для достижения целей. • Развитие критического мышления, что способствует осмыслению, оценки, анализу и синтезу информации, которые послужат основанием к действию. • Оценивание обучения, развития собственного понимания и определения обучения, для дальнейшего совершенствования. 2. Приёмы формирования математической грамотности . Формирование математической грамотности - сложный, многосторонний, длительный процесс. Достичь нужных результатов можно лишь умело, грамотно сочетая различные современные образовательные технологии. Технология критического мышления Цель: развитие мыслительных навыков учащихся, необходимых не только в учебе, но и в дальнейшей жизни (умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений). Использование технологии критического мышления очень эффективно на уроках математики. Оно развивает умение работать с информацией, логически мыслить, решать проблемы, аргументировать свое мнение, самообучаться, сотрудничать и работать в группе. Учитель и ученик меняются ролями, главная роль принадлежит ученику, а учитель — консультант, помощник. Ученикам очень нравится составлять кластер по разным темам, задание на возвращение к "известной информации", прием "мозаика, инструкции, памятки", вопросы верно или не верно, прием "корзина идей" для отработки навыка решения задач. Данная технология предполагает использование на уроке трех этапов: 1 этап - "Вызов", на котором ребѐнок ставит перед собой вопрос «Что я знаю?» по данной проблеме. 2 этап - "Осмысление": ответы на вопросы, которые сам поставил перед собой на первой стадии (что хочу знать). 3 этап - "Рефлексия", предполагающая размышление и обобщение того, «что узнал» ребенок на уроке по данной проблеме. Технология проблемного обучения Успешность проблемного обучения обеспечивается совместными усилиями преподавателя и обучаемых. Основной дидактический прием – создание проблемной ситуации, имеющей форму познавательной задачи. Познавательные задачи должны быть доступны по своей трудности, учитывать познавательные возможности обучаемых, находиться в русле изучаемого предмета и быть значимыми для усвоения нового материала. Функции обучающихся - не просто переработать информацию, а активно включиться в открытие неизвестного для себя знания. Основная задача педагога - не столько передать информацию, сколько приобщить учащихся к объективным противоречиям развития научного знания и способам их разрешения. В сотрудничестве с преподавателем учащиеся «открывают» для себя новые знания, постигают теоретические особенности отдельных предметов. Эффективными проблемными методами являются диалогические методы: побуждающий и подводящий диалоги. Проектная технология Это совместная учебно-познавательная, творческая или игровая деятельность, имеющая общую цель, согласованные методы и способы деятельности, направленные на достижение результата – создание проекта. Данная технология развивает у школьников умения самостоятельно конструировать свои знания и ориентироваться в информационном пространстве, проявлять компетенцию в вопросах, связанных с темой проекта, развивать критическое мышление. Целью проектной деятельности является создание творческого продукта, который позволяет решить ряд задач: расширить систему образов и представлений, развить познавательные навыки, навыков презентации и рефлексии деятельности. Роль учителя - это роль куратора, советника, наставника, но не исполнителя. Цель проектного обучения: овладеть общими умениями и навыками в процессе творческой самостоятельной работы, а также развить социальное сознание. Игровая технология Использование на уроках игровой технологии обеспечивает достижение единства эмоционального и рационального в обучении. Здесь происходит получение и обмен информацией, формируются навыки общения и взаимодействия. Включение в урок игровых моментов делает обучение более интересным, создает у учащихся хорошее настроение, облегчает процесс преодоления трудностей в обучении. Их можно использовать на разных этапах урока. С целью активизации знаний, развития познавательного интереса и творческой активности в начале урока эффективно использовать загадки, ребусы, кроссворды. При закреплении изученного материала. Игра – это частица детской жизни. В игре ребенок действует не по принуждению, а по внутреннему побуждению. Цель игры – сделать напряженный, серьезный труд занимательным и интересным для учащихся. Компьютерные технологии создают большие возможности активизации познавательной деятельности. Информационные технологии помогают отправиться в различные "путешествия", в которых ученики превращаются в пытливых искателей знаний. Работа с компьютером вызывает у детей повышенный интерес и усиливает мотивацию обучения. Использование компьютерных технологий создает возможность доступа к современной, свежей информации, осуществления "диалога" с источником знаний, к новой форме оценки знаний. Средства мультимедиа позволяют обеспечить наилучшую, по сравнению с другими техническими средствами обучения, реализацию принципа наглядности. Успешность, как один из основных мотивов, обеспечивается тем, что компьютерные программы позволяют сделать обучение интересным и разнообразным по форме. Информационно-коммуникационная технология В рамках работы по формированию математической грамотности эта технология особенно актуальна. Это, прежде всего, работа с разными источниками информации Важным преимуществом технологии является наглядность, так как большая доля информации для детей школьного возраста усваивается с помощью зрительной памяти, и воздействие на неѐ очень важно в обучении. Наиболее популярным здесь является использование возможностей мультимедийной презентации Но здесь важно не увлекаться. Презентация не самоцель, она должна выделять основные моменты темы. Здоровьесберегающая технология Неотъемлемой частью работы учителя является применение здоровьесберегающей технологии, которая позволяет создать на уроке зону психологического комфорта. Здесь наряду с учетом дозировки учебной нагрузки, соблюдением гигиенических требований, благоприятным эмоциональным настроем, включением оздоровительных моментов, хочу отметить важность смены видов деятельности на уроке, позволяющие преодолеть усталость, уныние, неудовлетворительность. Личностно-ориентированная технология На личностно-ориентированном уроке создается учебная ситуация, когда не только излагаются знания, но и раскрываются, формируются и реализуются личностные особенности учащихся. Здесь важно создать эмоционально положительный настрой учащихся на работу. Особенностями этой технологии являются: Продумывание учителем возможностей для самостоятельного проявления учеников; предоставления им возможности задавать вопросы, высказывать оригинальные идеи и гипотезы. Организация обмена мыслями, мнениями, оценками; стимулирование учащихся к дополнению и анализу ответов товарищей. Стремление к созданию ситуации успеха для каждого обучаемого. Побуждение учащихся к поиску альтернативной информации при подготовке к уроку. Один из приемов работы – вариативные домашние задания, что даѐт возможность каждому ученику проявить себя, свои сильные стороны, тем самым делая более позитивным отношение ребят к обучению в школе. 3. Поэтапное развитие различных умений, составляющих основу математической грамотности
Усвоения базисных основ математики, в большинстве своем, происходит в 5-6 классах, поэтому важно, чтобы на данном этапе обучения на первом плане стояло развитие математической грамотности учащихся. Что в дальнейшем поспособствует более глубокому и сознательному пониманию математики, как части общечеловеческой культуры. Обучающиеся часто задаются вопросами: зачем им математика, как она пригодится им в дальнейшем, как знания формул и теорем помогут им в повседневной жизни? Ответить на эти вопросы, а также показать ученикам связь математики с их будущей профессией, изменить их эмоционально-чувственное отношение к предмету позволяют задачи прикладного характера. Развивать математическую грамотность надо постепенно, начиная с 5 класса. Регулярно включать в ход урока задания на «изменение и зависимости», «пространство и форма», «неопределенность», «количественные рассуждения» и т.п.. Пример: работа в группах (целесообразно применять с целью формирования компетентностей самообразования и саморазвития) Каждая группа получает задание на карточке – две задачи. К каждой задаче необходимо составить выражение и решить задачу. Руководитель группы должен вывесить решение задачи на доске. Группа 1 1. Во время сбора урожая на поле, учащиеся 5 класса разделились на 4 звена по 5 человек в звене и 2 звена по 6 человек. Сколько всего учащихся в классе? 2. Собранный картофель распределили в 25 контейнеров по а килограмм в каждом и еще осталось 10000 килограммов. Сколько картофеля было собрано? Группа 2 1. Пшеницу на поле собирали два дня. За первый день было обмолочено 40 центнеров, а за второй – на 7 центнеров больше. Сколько центнеров пшеницы обмолотили за два дня? 2. Фермерское хозяйство “Трудяги” собрало 2600 кг огурцов, а их соседи “Непоседы” на k кг больше. Сколько килограммов огурцов собрали в фермерском хозяйстве “Непоседы”. Группа 3 1. Работники завода “Прогресс” в 2019 году выпустили 346 измерительных приборов, что на п приборов больше, чем в 2018 году. Сколько измерительных приборов было выпущено за два года? 2. Овощная база, получив помидоры, решила 2 тонны помидоров засолить для использования зимой, а свежими оставила в два раза меньше. Сколько всего помидоров получила овощная база. Эти задания можно использовать по усмотрению учителя: Как игровой момент на уроке; Как проблемный элемент в начале урока; Как задание – «толчок» к созданию гипотезы для исследовательского проекта; Как задание для смены деятельности на уроке; Как модель реальной жизненой ситуации, иллюстрирующей необходимость изучения какого либо понятия на уроке; Как задание, устанавливающее межпредметные связи в процессе обучения; Некоторые задания заставят сформулировать свою точку зрения и найти аргументы для её защиты; Можно собрать задания одного типа и провести урок в соответветствии с какой-то образовательной технологией; Можно все задачи объединить в группы и создать свой элективный курс по развитию математического мышления; Задания такого типа можно включать в школьные олимпиады, математические викторины; Задачи на развитие математического мышления могут стать основой для внеклассного мероприятия в рамках декады математики. Примеры заданий (связь с другими предметами) : Математика-физика 1. Послан человек из Москвы в Вологду, и велено ему в хождении своем совершать каждый день по 40 верст. На следующий день вслед ему послан второй человек, и приказано ему делать в день по 45 верст. Через сколько дней второй человек догонит первого? (Т.к первый вышел на день раньше и прошел 40 верст, то второму надо нагнать эти 40 верст. За 40:(45-40)=8 дней.) Автобус первые 4 км пути проехал за 12 мин, а следующие 12 км – за 18 мин. Определите среднюю скорость автобуса на всем пути. (32км/ч) Математика-биология 1. Мама-слониха имеет массу 600 кг. Найдите массу слонёнка, если известно, что она составляет 1/5 часть от массы большого слона. Математика-экономика 1. Рабочий купил компьютер за 11400 р. в кредит. При покупке он внёс 2/5 части от стоимости компьютера. Остальные деньги рабочий вносил в течение 10 месяцев. Сколько денег рабочий выплачивал ежемесячно? Математика-история 1. В московском Кремле находятся Царь-колокол и царь-пушка. Вес колокола 200 тонн, вес пушки 20% веса колокола Сколько тонн весит царь-пушка? Для выполнения заданий требуется относительно небольшой объем знаний и умений, которые необходимы для математически грамотного современного человека. К ним отнесены: пространственные представления; пространственное воображение; свойства пространственных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (в форме таблиц, диаграмм, графиков реальных зависимостей), характерную для средств массовой информации; умение работать с формулами; знаковые и числовые последовательности; нахождение периметра и площадей нестандартных фигур; действия с процентами; использование масштаба; использование статистических показателей для характеристики реальных явлений и процессов; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др. Можно применять полученные знания и умения на уроках к решению проблем, возникающих в повседневной практике Примеры заданий: Проблемная ситуация (работа в группах) (9 кл.) Составьте геометрическую прогрессию: 1. Ежедневно каждый болеющий гриппом может заразить четырех окружающих. Какой вывод мы можем сделать? 2. Дима на перемене съел булочку, не помыв руки. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 минут происходит деление бактерий (они удваиваются). Какой вывод мы можем сделать? 3. Каждый курильщик выкуривает в среднем 8 сигарет в сутки. После выкуривания одной сигареты в легких оседает 0,0002 грамма никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается в два раза. Какой вывод мы можем сделать? Задания из международного исследования PISA: 1. Какое время в Берлине, если в Сиднее 19:00? Решение. Из найденной Марком информации ясно, что сиднейское время на 9 часов опережает берлинское. Когда в Сиднее 19:00, в Берлине 10:00. Ответ: 10:00. 2. Длина шага P — расстояние от конца пятки следа одной ноги до конца пятки следа другой ноги. Для походки мужчин зависимость между n и P приближенно выражается формулой n/P = 140, где n — число шагов в минуту, P— длина шага в метрах. ВОПРОС 1. Используя данную формулу, определите, чему равна длина шага Сергея, если он делает 70 шагов в минуту. Решение. Из данной формулы получаем: n/P = 140 P⇔= n/140 . По условию Сергей делает 70 шагов в минуту, значит, n= 70. Длина его шага (в метрах ) равна P = 70/140 =0,5 . Ответ: 0,5 метров. 3. В пиццерии подают две круглых пиццы одной и той же толщины, но разных размеров. Меньшая имеет диаметр 30 см и стоит 30 денег. Большая имеет диаметр 40 см и стоит 40 денег. Какую из двух пицц выгоднее покупать? Приведите ваши рассуждения. Решение: Толщина двух пицц одинаковая, поэтому вычислим площадь каждой пиццы, предполагая, что это обычный круг. Площадь круга находится по формуле (где Найдем стоимость 1 см Для пиццы 30 см она составляет Для пиццы 40 см она составляет Покупка пиццы диаметром 40 см является более выгодной. Формирования функциональной грамотности на уроках математики невозможно без правильной и четкой математической речи. Для формирования грамотной, логически верной математической речи можно использовать составление математического словаря, написание математического диктанта, выполнение заданий, направленных на грамотное написание, произношение и употребление имен числительных, математических терминов. Например, во время устной работы может быть проведена следующая работа: математический диктант, выявляющий умение записывать числа. 4. Формирование финансовой грамотности Одной из составляющих математической грамотности является финансовая грамотность. В школьном курсе математики по ФГОС, разработанном Муравиными Ольгой Викторовной и Георгием Константиновичем, предлагается поэтапная схема введения практических знаний о финансах. То есть не обрушивать на старшеклассника сразу весь объем информации, а с начальной школы предлагать задачи, которые отображают финансовые операции. И хотя я работаю по УМК Ю.М. Калягина, считаю, что данная схема подходит ко всем учебникам математики. В начальной школе происходит знакомство с денежными знаками, ценой и стоимостью товаров. Младшие школьники учатся пользоваться карманными деньгами: оплачивать обеды в школе, рассчитывать сдачу. Дети знакомятся с товарами. Теперь, запоминая информацию о себе, ребенок сможет назвать не только свое имя, возраст, но и, например, размер одежды. В 4 классе во время изучения долей предлагается составить диаграмму, отображающую бюджет семьи. Так ребенок впервые увидит, как распределяются средства. Уже в 5 классе эта диаграмма приобретет новый вид — теперь статьи расходов будут отображаться в процентах. Научившись рассчитывать проценты, ученики смогут понять, как работает система кредитования и вкладов, как начисляются премии. В 6 классе, познакомившись с пропорциями, ученики наблюдают, как снижаются или повышаются цены на те или иные товары, как зависит уплата налогов от заработной платы. Деление в данном отношении позволяет рассмотреть проблему распределения прибыли пропорционально внесенным деньгам, оплаты за выполненную работу. Изучение функций и их систем в 7 классе дает возможность ввести огромное количество новых, уже более сложных понятий: спрос и предложение, рыночное равновесие, равновесная цена. Ученики начинают рассчитывать оптимальные затраты на покупки и услуги. Задачи формулируются таким образом, чтобы спровоцировать обсуждение конкретной жизненной ситуации, так например, школьник должен в полной мере осознать, какова вероятность выиграть в лотерею, и к каким неоправданным тратам приведет его регулярное в ней участие. В 8 классе вновь вернемся к кредитам и вкладам: квадратные уравнения объяснят ситуацию с изменением процентов по вкладу, двухгодичных кредитов и депозитов с фиксированным годовым процентом. 9 класс позволяет еще больше углубиться в эту тему: изучение степени с целым показателем и формулы суммы геометрической̆ прогрессии поможет вывести формулы депозита и кредита. Имеет смысл начать говорить об ипотечном кредитовании, покупке и продаже акций. В 10-11 классах при введении математического анализа ученикам будут предложены более сложные банковские задачи с использованием показательной и логарифмической функций; производной; наибольшего и наименьшего значения. Учителю важно осознать, что на протяжении всего обучения решение подобных задач должно сопровождаться дискуссией и приводить учеников к самостоятельным выводам о том, как правильно распоряжаться финансами. Только в этом случае можно говорить не только о практическом применении знаний, но и именно о формировании финансовой грамотности. Примеры задач на уроках математики: 1. Стоимость автомобиля “Рено-Логан” составляет 600 000 рублей. В соответствии с условиями кредитования, при его покупке покупатель выплачивает половину стоимости, а второю половину можно выплатить в течении двух лет равными частями. При этом банку необходимо заплатить только одноразовую комиссию в сумме 2,5% от суммы кредита. Также необходимо обязательно застраховать автомобиль, стоимость страховки составляет 5% от стоимости автомобиля. Какую общую сумму за автомобиль необходимо уплатить? Сколько денег ежемесячно необходимо выплачивать банку? Решение: 1. 600000 : 2 = 300000 (руб.) - половина суммы; 2. 2,5% = 0,025 300000 ∙ 0,025=7500 (руб.) - одноразовая комиссия; 3. 5% = 0,05 600000 ∙ 0,05 =30000 (руб.) страховка 4. 600000 + 7500 + 30000 = 637500 (руб.) - общая сумма; 5. 300000 + 7500 + 30000 = 337500 (руб.) сумма, которую необходимо уплатить на протяжении двух лет; 6. 337500 : 24 = 14062,5 (руб.) – ежемесячная выплата. Ответ: 637500 руб.; 14062,5 руб. 2. Деньги в сумме 140000 рублей, собранные во время благотворительного концерта были распределены следующим образом: 45% отправили в детский дом, 42,5% - в дом инвалидов, а на остальные деньги купили для музыкальной школы духовые инструменты. Сколько стоят духовые инструменты? Решение: 1. 100% - (45% + 42,5%) = 12,5% - стоимость духовых инструментов; 2. 12,5% = 0,125 140 000 ∙ 0,125 = 17500(руб.) – стоимость духовых инструментов. Ответ: 17500 руб. 3. Для того, чтобы получить автомобильную краску цвета “Красный мак”, необходимо взять основу, прибавить 22% красной краски, 10% коричневой, 1,5% чёрной, 3% желтой. 3% золотой краски и 5% затвердителя. Какой объем основы нужен для изготовления 4 л краски? Решение I способ 1. 22% + 10% + 1,5% + 3% +3% + 5 % = 41,5% - добавки; 2. 100% - 41,5% = 58,5% - основа; 3. 58,5% = 0,585 4 ∙0,585 = 2,34 (л) основа Ответ: 2,34 л. II способ 1. 22% + 10% + 1,5% + 3% +3% + 5 % = 41,5% - добавки; 2. 100% - 41,5% = 58,5% - основа; 2. Пусть х л – это основа, которую необходимо взять 100% - 4 л 58,5% - х л По свойству прямо пропорциональных величин имеем: 2,34 (л) Ответ: 2,34 л. Все эти задания направлены на развитие математической и естественнонаучной грамотности, которое предполагает способность учащихся использовать знания, приобретенные ими за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе. На своих уроках для повышения мотивации учащихся и формирования математической грамотности я достаточно часто использую задания из разных источников, в том числе и конкурсные задачи по математике, при решении которых основное внимание уделяется формированию способностей учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции. В качестве примера хочу привести задания из математических конкурсов, которые направлены на проверку умений выполнять перевод единиц из одной измерительной системы в другую и могут быть использованы для учащихся с 7 – 11 класс. 1. Из числа всей её челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырём и глухонемой от рожденья». Тургенев И.С. «Муму» В то время при определении роста человека счёт вёлся от двух аршин (обязательных для обычного взрослого человека). 1 аршин = 71 см. 1 вершок = 45 мм. Каков был рост Герасима? 1. Найдём, чему равны 2 аршина в сантиметрах. 2. Найдём, сколько миллиметров в 12 вершках. 3. Переведём миллиметры в сантиметры. 4. Вычислим весь рост Герасима в сантиметрах. 2. В 1912 году инженер МакМэхон задумал строительство небоскрёба высотой 480 футов. Однако в контракте на постройку высота была указана не в футах, а в дюймах, чего заказчики не заметили. В результате получилось 4-этажное здание высотой несколько метров. Сейчас это здание называют самым маленьким небоскрёбом в мире. Вопрос А: Сколько метров в высоту должно было быть здание по первоначальному плану? Запиши только число. Вопрос Б: Сколько метров в высоту получилось здание? Запиши только число. Подсказка: 1 фут = 0,3 м, 1 дюйм = 25 мм Задания в ОГЭ по математике тоже принимают характер прикладной направленности, но в учебниках их по-прежнему очень мало. поэтому я подключаю различные источники для поиска и внедрения в учебный процесс подобных задач. В основной школе на современном этапе ученик поставлен в центр учебного процесса. Внимание акцентируется на развитии ученика, формировании его мотивационной сферы и независимого стиля мышления. Математика как школьный предмет обладает достаточным потенциалом для формирования и развития этих качеств. Поэтому содержание стандарта, в частности, математического образования должно способствовать тому, чтобы математическая грамотность была на высоком уровне. Приложения (задачи прикладного характера) Задача «Апартаменты для отдыха» Асель нашла эти апартаменты для отдыха, выставленные на продажу в интернете. Она думает купить апартаменты для отдыха, так чтобы она могла сдавать их в аренду отдыхающим.
Вопрос 1: АПАРТАМЕНТЫ ДЛЯ ОТДЫХА Для того, чтобы оценить стоимость апартаментов для отдыха, Асель обратилась к эксперту за оценкой. Для оценки стоимости апартаментов для отдыха, эксперт использует следующие критерии:
Если стоимость, определенная экспертом будет выше рекламной стоимости, то для Асель, как потенциальному покупателю, цена будет «очень хорошей». Покажите, опираясь на критерии эксперта, что продажная цена предложенного жилья «очень хорошая» для Асель. Ответ :Ответ, который показывает, что предполагаемое значение согласно критериям эксперта 210000 зедов. Вопрос 2: АПАРТАМЕНТЫ ДЛЯ ОТДЫХА За последние 10 лет отдыхающие использовали апартаменты в среднем 315 дней в году. Можно ли вывести следующие утверждения из данной информации. Обведите “Да” или “Нет” для каждого утверждения.
Примечание: Считайте, что в году 365 дней. Ответ: Три полных ответа: Нет, Нет, Да, в этом порядке. ОКРУГЛЕНИЕ(5 кл) Алисе необходимо найти сумму чисел 19,6,23,8 и 38,4, округлив их до ближайшего целого числа. Какие три числа ей взять? ЯБЛОНИ (9 класс тема прогрессия) Фермер на садовом участке высаживает яблони в форме квадрата, как показано на рисунке. Для защиты яблонь от ветра он сажает по краям участка хвойные деревья. Ниже на рисунке изображены схемы посадки яблонь и хвойных деревьев для нескольких значений n, где n – количество рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа n. 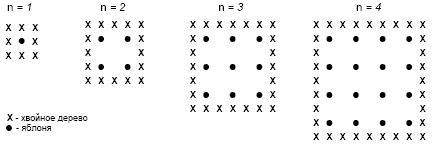 Вопрос 1: Заполните таблицу: 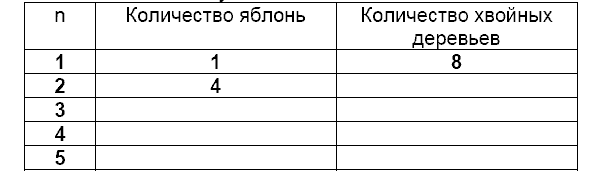 Вопрос 2: В рассмотренной выше последовательности количество посаженных яблонь и хвойных деревьев подсчитывается следующим образом: количество яблонь = n2, количество хвойных деревьев = 8n, где n – число рядов высаженных яблонь. Для какого значения n число яблонь будет равно числу посаженных вокруг них хвойных деревьев? Запишите решение. Вопрос 3: Предположим, что фермер решил постепенно увеличивать число рядов яблонь на своем участке. Что при этом будет увеличиваться быстрее: количество высаживаемых яблонь или количество хвойных деревьев? Запишите объяснение своего ответа. Литература: Филатова, М. Н. Внеурочная деятельность учащихся как средство достижения личностных и метапредметных результатов в условиях реализации ФГОС / М. Н. Филатова. — Текст : непосредственный // Молодой ученый. — 2015. — № 16 (96). — С. 430-434. — URL: https://moluch.ru/archive/96/21584/ (дата обращения: 08.10.2020). Образовательная система «Школа 2100». Педагогика здравого смысла / под ред. А. А. Леонтьева. М.: Баласс, 2003. Cимонова О. В. Формирование функциональной грамотности при обучении математике в 5–6-х классах общеобразовательной школы // Вестник Вятского государственного гуманитарного университета – 2010. – № 3. – С. 147–153. Басюк В. С., Ковалева Г. С. Инновационный проект Министерства просвещения «Мониторинг формирования функциональной грамотности»: основные направления и первые результаты // Отечественная и зарубежная педагогика. 2019. Т. 1, № 4 (61). С. 13–33. Рослова Л. О., Краснянская К. А., Квитко Е. С. Концептуальные основы формирования и оценки математической грамотности // Отечественная и зарубежная педагогика. 2019. Т. 1, № 4 (61). С. 58–79. |

 Цена: 200 000 зед
Цена: 200 000 зед