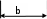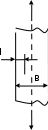тюменский индустриальный университет Институт сервиса и отраслевого управления кафедра техносферной безопасности определение долговечности подкрановой балки по дисциплине Конструкционная безопасность
 Скачать 81.99 Kb. Скачать 81.99 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственной бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Институт сервиса и отраслевого управления КАФЕДРА ТЕХНОСФЕРНОЙ БЕЗОПАСНОСТИ ОПРЕДЕЛЕНИЕ ДОЛГОВЕЧНОСТИ ПОДКРАНОВОЙ БАЛКИ по дисциплине «Конструкционная безопасность» 20 вариант Выполнил: обучающийся группы БТПб-17-2 Соболев Никита Вадимович Проверил: Старший преподаватель кафедры «Техносферная безопасность» Александров Сергей Вячеславович Тюмень,2020 Определение долговечности подкрановой балки Исходные данные Необходимо определить время до проведения ремонтных работ на подкрановой балке, рассчитанной с запасом по пределу прочности nB =2,6 (σB= 500 МПа). Предел текучести балки σт =240 МПа. Балка нагружается в течение месяца 4*104 раз. В полке балки после её изготовления была обнаружена трещина длиной 0,012 м. При циклических испытаниях образца шириной B= 0,19 м и с боковой трещиной l = 0,016 м при напряжениях σ= 187 МПа трещина за первые ΔN1 = = 104 циклов увеличилась на Δl1 =0,0014 м, за вторые ΔN2 = 104 циклов – на Δl2 =0,0028 м. Разрушение образца произошло при длине трещины lc=0,027 м. Запас прочности балки не должен быть ниже 1,5. Постановка задачи Нагрузки на подкрановую балку и форма сечения в условиях задачи не заданы, поэтому примем произвольно, что сечение подкрановой балки – двутавр №60с
Требуется оценить долговечность балки в условиях циклического нагружения. Для оценки долговечности конструкции воспользуемся результатами испытаний плоского образца с боковой трещиной
Указанный в условии задачи предел прочности σB= 500 МПа соответствует обычным конструкционным сталям, соответственно можно принять предел текучести σт =240 МПа. Эксплуатационное напряжение примем равным допускаемому по условию статической прочности. 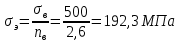 Основные уравнения При оценке долговечности конструкции с трещиной, в условиях циклического нагружения, основной характеристикой является скорость роста трещины 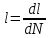 зависящая от многих параметров. В результате многочисленных экспериментов было установлено, что основным параметром, определяющим l, является размах коэффициента интенсивности напряжений (КИН) ΔK, вычисляемый по размаху напряжений в растягивающей части цикла[3]. зависящая от многих параметров. В результате многочисленных экспериментов было установлено, что основным параметром, определяющим l, является размах коэффициента интенсивности напряжений (КИН) ΔK, вычисляемый по размаху напряжений в растягивающей части цикла[3].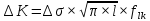 (1) (1)где 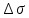 – размах напряжений в растягивающей части цикла; – размах напряжений в растягивающей части цикла;l – длина трещины образца; 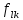 – коэффициент, зависящий от соотношения размеров образца и трещины. – коэффициент, зависящий от соотношения размеров образца и трещины.В случае односторонней боковой трещины 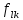 вычисляется по формуле (2). вычисляется по формуле (2).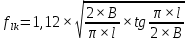 (2) (2)где B – ширина образца. Размах напряжений при испытаниях определяется по формуле (3). 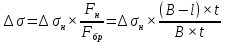 (3) (3)где 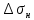 – напряжение при испытаниях образца; – напряжение при испытаниях образца;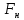 – площадь полки балки, с учетом трещины (площадь брутто); – площадь полки балки, с учетом трещины (площадь брутто);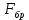 – площадь без учета трещины (площадь брутто); – площадь без учета трещины (площадь брутто);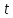 – высота полки балки. – высота полки балки.Связь 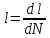 и и 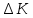 определяется уравнением Переса. определяется уравнением Переса.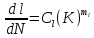 (4) (4)Где 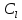 и и 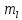 – характеристика материала и условий нагружения. – характеристика материала и условий нагружения.После замены 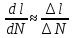 и логарифмирования уравнения (4) получим: и логарифмирования уравнения (4) получим: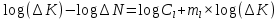 (5) (5)Зависимость длины трещины от числа циклов получают интегрированием уравнения (4). Коэффициент 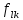 , зависящий от l, изменяется незначительно, для упрощения его можно принять постоянным, равным некоторому среднему значению , зависящий от l, изменяется незначительно, для упрощения его можно принять постоянным, равным некоторому среднему значению 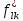 . .Подставив (1) в (4) и проинтегрировав получим: 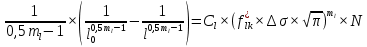 (6) (6)В расчете учитываем протяженность пластической зоны у кончика трещины, подставляя в формулы (1) и (2) вместо 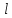 условную длину трещины условную длину трещины 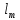 , определяемую по формуле (7). , определяемую по формуле (7).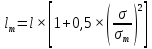 (7) (7)где 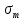 - предел текучести - предел текучести Определение параметров Сl и ml. Построение зависимости l~ N для образца. Параметры Сl и mlопределяются по результатам испытания образца. Размах напряжений при испытаниях задан по площади нетто. По формуле (3) вычисляем напряжение по площади брутто: 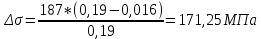 Находим условную длину трещины для l1=0,016 м: 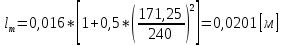 Рассчитаем flk по формуле (2). Тангенс угла рассчитывается в радианах. 1 градус = 0,017 радиан. 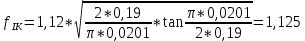 Рассчитываем размах КИН по формуле (1): 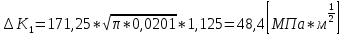 Повторяем расчеты для длины трещины после N1 циклов нагружений: 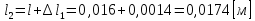 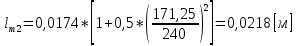 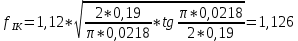 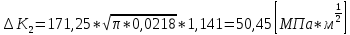 Запишем уравнения (5) для первых и вторых 104 циклов: 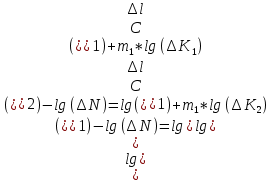 Подставляя численные значения, получаем систему уравнений для определения Сl и ml : 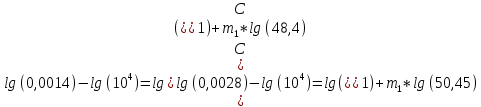 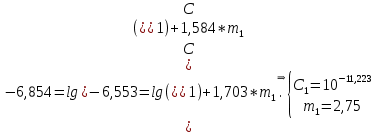 Зная С1 и m1 по уравнению (6) можно найти число циклов до разрушения образца. Длина трещины в момент разрушения lc=0,027 м. Вычисляем: 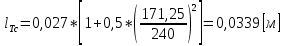 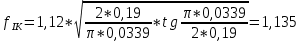 При изменении длины от 0,016 м до 0,027 м 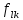 изменяется от 1,125 до 1,135. изменяется от 1,125 до 1,135.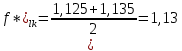 Подставляем найденные величины в уравнение (6): 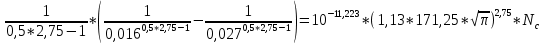 Откуда получаем Nc=6,94*104 циклов. По найденным значениям строим зависимость l~ N (Рис.2.1). 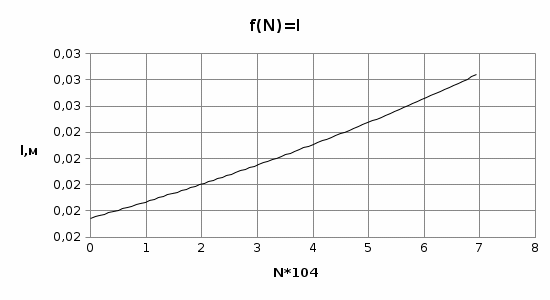 Рис.2.1 График зависимости l~ N для образца Оценка долговечности подкрановой балки. Для оценки долговечности балки используем формулу (6). Предварительно определяем, какая трещина на образце будет соответствовать заданному размеру трещины на балке из условия пропорциональности размеров: 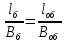 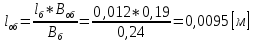 Уровень долговечности эксплуатируемых напряжений известен- 192,3 МПа. Определим критическую длину трещины, соответствующую этим напряжениям, используя условие постоянства критического размаха КИН. По формуле (1) ΔКIc для образца: 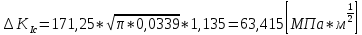 Вычисляем критическую длину трещины при напряжении Δσэ=192,3 МПа: 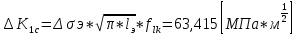 В этом равенстве 2 неизвестных, так как 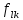 зависит от l. зависит от l.Решаем подбором. Принимаем, что 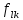 =1,135, что соответствует lc=0,027. =1,135, что соответствует lc=0,027.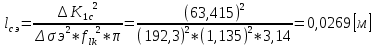 Соответствующий коэффициент 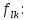 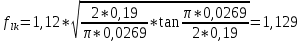 Для повторного приближения примем: 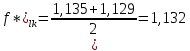 2) 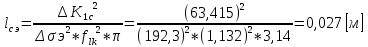 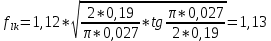 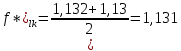 3) 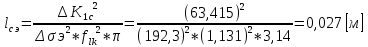 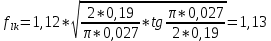 lcэ перестало изменяться с округлением до тысячных. Приближения можно прекратить. Окончательно, после приближений - 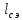 =0,027 м. =0,027 м.Так как величина 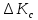 определена с учетом пластической зоны, поэтому найденная величина трещины является условной. Используя формулу (3) найдем критическую длину трещины. Принимая: определена с учетом пластической зоны, поэтому найденная величина трещины является условной. Используя формулу (3) найдем критическую длину трещины. Принимая: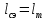 . .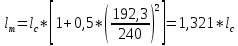 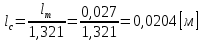 При изменении длины от  =0,0095 м до =0,0095 м до 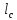 = 0,0204 м коэффициент = 0,0204 м коэффициент 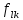 изменяется от 1,121 до 1,13. изменяется от 1,121 до 1,13.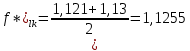 Подставляя все найденные величины в формулу (6), находим критическое число циклов в условиях эксплуатации балки. 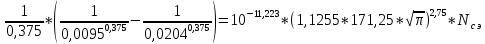 Откуда получаем Ncэ=6,921*104 циклов. Запас по числу циклов nN рекомендуется 5 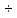 20. Примем nN=10. 20. Примем nN=10.Находим допускаемое число циклов: 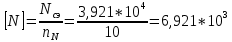 Проверка прочности по напряжениям По условию запас прочности по напряжению должен быть не менее nσ=1,5. Проверим, выполняется ли условие. Определяем длину трещины, соответствующей N=[N] по формуле (6). 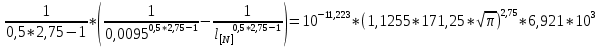 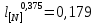 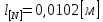 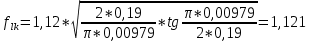 Находим, какое критическое напряжение соответствует этой длине трещины: 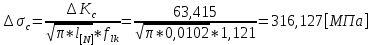 Запас прочности: 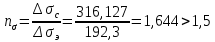 Условие прочности соблюдается. Заключение. Допустимое число циклов нагружения для подкрановой балки с трещиной [N]=6,921*103. За месяц балка испытывает 4*104 нагружений. Ремонт необходим примерно через 5 дней. Список использованных источников Махутов Н. А., Пермяков В. Н. Механика деформирования и разрушения нефтегазохимических объектов: Учебное пособие Тюмень: ТюмГНГУ, НТЦ НГП, 2012. – 176с. Махутов Н. А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. – М.: Машиностроение, 1981. Когаев В. П., Махутов Н. А., Гусенков А. П., Расчеты деталей машин и конструкций на прочность и долговечность. Спарвочник. - М.: Машиностроение, 1985. Махутов Н.А. Конструкционная прочность, ресурс и техногенная безопасность. Часть 1: Критерии прочности и ресурса. Новосибирск: Наука, 2005. - 494 с. Махутов Н.А. Конструкционная прочность, ресурс и техногенная безопасность. Часть 2: Обоснование ресурса и безопасности. Новосибирск: Наука, 2005. - 610 с. |