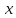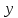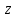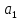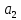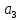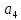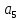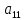Дискретная математика СибГУТИ. Контр. дискрет. U и множества A, B, C, D. Найти результаты действий a д и каждое действие проиллюстрировать с помощью диаграммы ЭйлераВенна. U A b c d . Решение
 Скачать 5.95 Mb. Скачать 5.95 Mb.
|
|
I. Задано универсальное множество U и множества A, B, C, D.  Найти результаты действий a) - д) и каждое действие проиллюстрировать с помощью диаграммы Эйлера-Венна. Найти результаты действий a) - д) и каждое действие проиллюстрировать с помощью диаграммы Эйлера-Венна.U = 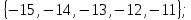 A = 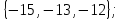 B = B = 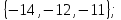 C = C = 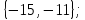 D = D = 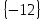 . .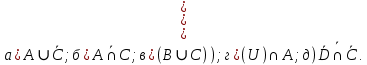 Решение. а) 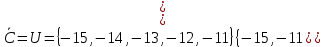 = = 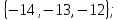 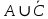 = = 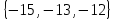 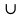 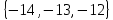 = = 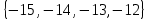 . .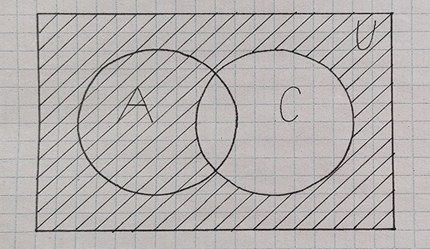 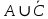 б) 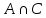 = = 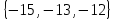 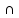 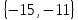 = = 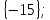 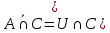 = = 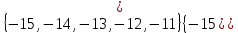 = =  = 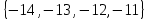 . .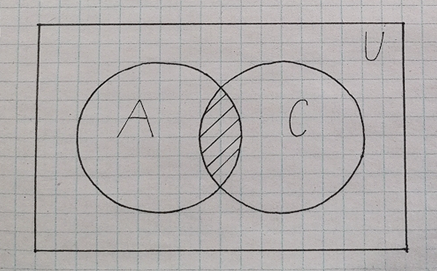 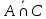 в) 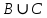 = = 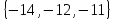 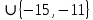 = = 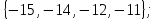 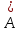 = =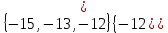 = = 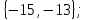 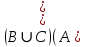 = = 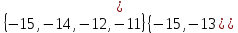 = =  . .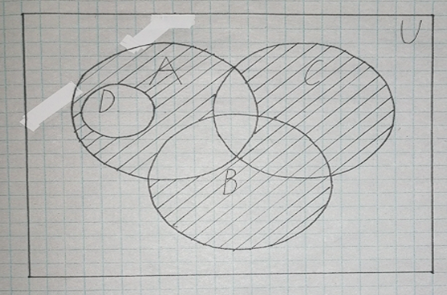 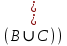 г) 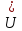 = = 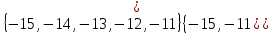 = = 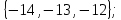 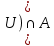 = = 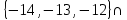 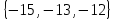 = = 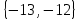 . .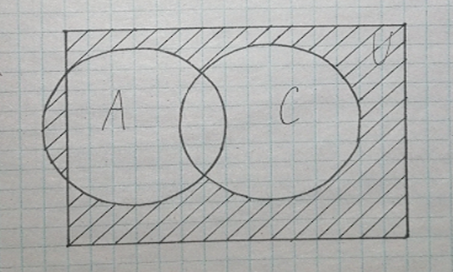 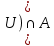 д) 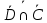 = = 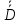 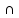 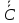 = =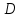 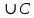 = = 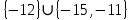 = = 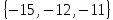 . .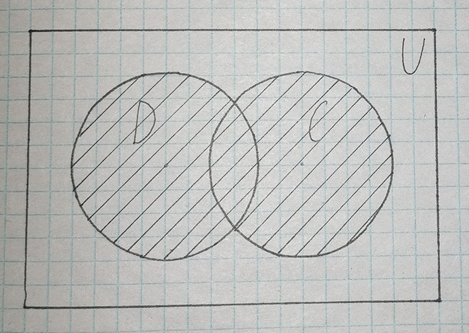 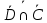 II. Ввести необходимые элементарные высказывания и записать логической формулой следующее предложение. “Если оперативная память правильно установлена в контрольный компьютер, и он при запуске не выдает ошибки при проверке оперативной памяти, то оперативная память исправна”. Решение. Введем обозначения для высказываний: 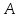 = «Оперативная память правильно установлена в контрольный компьютер»; = «Оперативная память правильно установлена в контрольный компьютер»;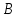 = «Контрольный компьютер при запуске не выдает ошибки при проверке оперативной памяти»; = «Контрольный компьютер при запуске не выдает ошибки при проверке оперативной памяти»;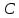 = «Оперативная память исправна». = «Оперативная память исправна».Искомая логическая формула имеет вид: 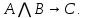 III. Для булевой функции 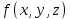 найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему. найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему.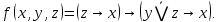 Решение. Методом преобразования получили: 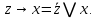 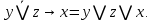 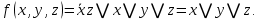 Произошла операция поглощения: 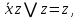 получена минимальная ДНФ. получена минимальная ДНФ.Строим таблицу истинности:
Запишем СКНФ функции: 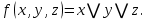 Релейно-контактная схема, имеет вид: 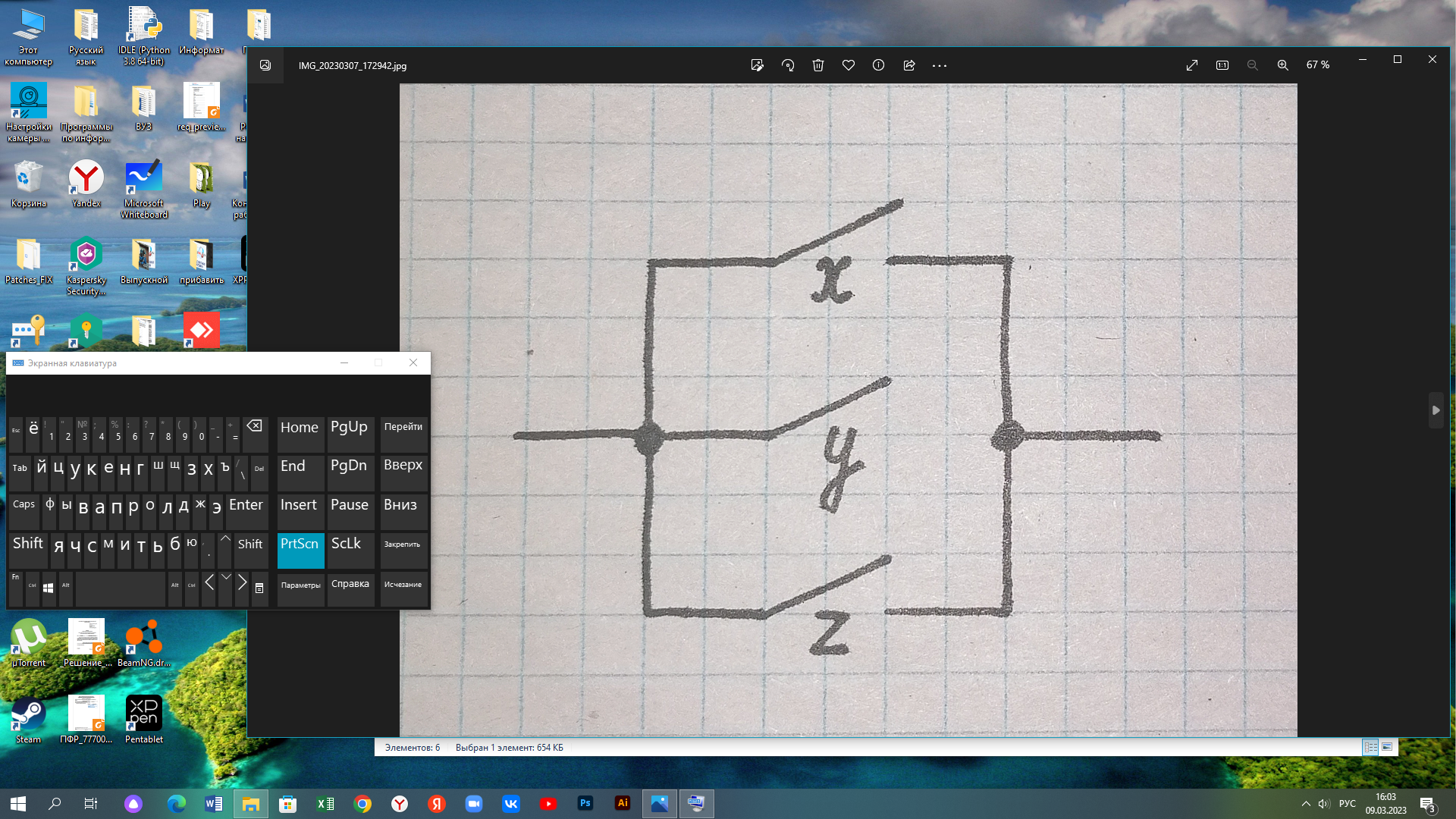 IV. Орграф задан своей матрицей смежности. Следует: а) нарисовать орграф; б) найти полустепени и степени вершин; в) записать матрицу инцидентности; 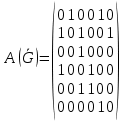 Решение. а) Орграф на плоскости имеет вид:  б) Находим полустепени и степени вершин. Полустепени исхода для вершин орграфа: 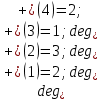 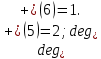 Полустепени захода для вершин орграфа: 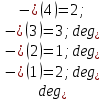 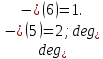 Степень любой вершины орграфа равна сумме полустепеней для этой вершины 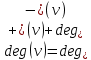 . Имеем: . Имеем: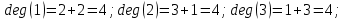 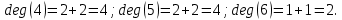 Сумма всех степеней орграфа равна 22. Разделив это число на 2, получим 11 - число ребер орграфа. в) Запишем матрицу инцидентности орграфа. Это матрица размера 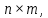 где где 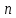 - число вершин, - число вершин, 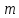 - число дуг орграфа. Элементы - число дуг орграфа. Элементы 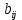 матрицы вычисляют по правилу: матрицы вычисляют по правилу: 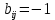 , если дуга , если дуга 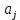 входит в вершину входит в вершину 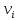 ; ; 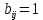 , если дуга , если дуга 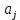 выходит из вершины выходит из вершины 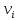 ; ; 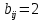 , если дуга , если дуга 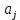 есть петля вершины есть петля вершины 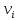 ; ; 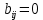 , если , если 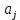 и и 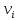 не инцидентны. не инцидентны.
|