Программа курса _Математическая логика_. Учебная программа курса Математическая логика
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
СОДЕРЖАНИЕ КУРСА «МАТЕМАТИЧЕСКАЯ ЛОГИКА»(6 КЛАСС)Простые логические высказывания. Логические связки. Истинность и ложность простых логических высказываний. Сложные логические высказывания. Формирование сложных логических высказываний из простых логических высказываний с помощью логических связок. Истинность и ложность сложных логических высказываний. Множество и элемент множества. Задание множеств. Примеры конечных и бесконечных множеств. Подмножества. Разбиение множества. Пересечение, объединение, разность множеств. Иллюстрация отношений между множествами с помощью кругов Эйлера. Понятие логических задач. Выделение в задаче данных и искомых величин. Построение цепочек. Доказательство истинности или ложности утверждений. Решение логических задач по темам: Переправы и разъезды. Остров рыцарей и лжецов. На взвешивания. Фальшивые монеты. Расположения, перекладывания. Дележи при затруднительных обстоятельствах. Выигрышные и проигрышные позиции. Парадоксы и софизмы. Комбинаторные задачи. Решение комбинаторных задач методом полного перебора вариантов. Правила сложения и умножения в комбинаторике. Решение комбинаторных задач на применение этих правил. Вероятность и статистика. События. Случайное событие. Достоверное и невозможное события. Сравнение шансов событий. Вероятностная шкала. Статистические данные. Таблицы и диаграммы. Вероятность события. Подсчёт вероятностей. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ КУРСА «МАТЕМАТИЧЕСКАЯ ЛОГИКА» В 6 КЛАССЕ (34 часа)
ПРИЛОЖЕНИЕ 5 класс Проверочная работа №1. В записи 5*6*7*8 замените звёздочки знаками действий так, чтобы получилось выражение, значение которого равно 39. Восстановите магический квадрат:
Найдите правило нахождения чисел, помещённых на «голове». Поставьте число в свободный кружок. 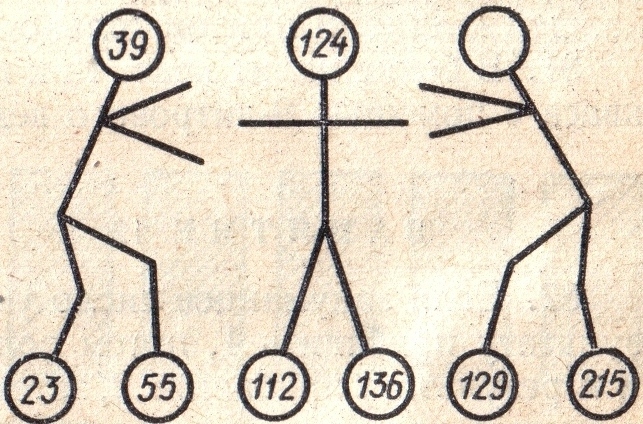 От Земли до Марса около 60 млн. км. Сколько времени придется лететь на ракете от Земли до Марса, если скорость ракеты будет 10 км/с? Сколько времени потребовалось бы самолету, летящему со скоростью 1 000 км/ч, чтобы пролететь это расстояние? Проверочная работа №2 Папа обещал Васе: «Летом мы с тобой поедем в город Тверь или в город Киев». Наступило лето, и они поехали в город Самару, а в города Тверь и Киев не поехали. Обманул и папа Васю? В каком случае папа не обманул бы Васю? Запишите все числа, которые можно составить, используя только две римские цифры I и V. Некоторые перчатки шьют из кожи. Все новые кожаные изделия немного жмут, но некоторые со временем делаются мягче. Таким образом: а) все перчатки немного жмут, пока они новые; б) некоторые перчатки со временем становятся мягче; в) только мягкая, немного поношенная кожа используется для изготовления перчаток. Какие из этих утверждений верны? Проверочная работа №3 Обведите красным карандашом множество чисел {9;0;5;2;7}, а синим карандашом множество чисел {1;7;3;0;4:6} 2 6 7 1 9 1 3 4 0 Запишите с помощью фигурных скобок и символов U, ∩ множество общих элементов красного и синего множеств; множество всех элементов данных множеств.   К О 1 М 3 К С ∆ А а) Сколько элементов в красном множестве, в синем множестве; только в красном множестве; только в синем множестве? б) Сколько общих элементов в этих множествах? Сколько всего элементов в обоих множествах? В пересечении двух множеств – 2 элемента, в объединении – 4 элемента. Сколько элементов в каждом из этих множеств? Даны два множества.         Снимите 2 фишки так, чтобы в каждом из множеств было по три элемента. Снимите одну фишку так, чтобы в каждом из множеств было по три элемента. Не снимая ни одну из фишек. Сделайте так, чтобы в каждом множестве было по три элемента. Проверочная работа №4 На рисунке даны точки E, T, O, V. Отметьте точку М так, чтобы оба высказывания MэEO и MэTV были истинными. (EO и NV – отрезки).    E  V T O Начертите ломаную ERVM. Проведите отрезок DQ так, чтобы выполнялось условие ERVM∩DQ={A,B,C} На рисунке изображены окружность R = 3 и ломаная KLFD. Что является пересечением этой ломаной и круга, изображенного на рисунке? D  Q H F S K Проверочная работа №5 На уроке физкультуры ученики выстроились в линейку на расстоянии одного метра друг от друга. Вся линейка растянулась на 25 метров. Сколько было учеников. Зажгли 7 свечей, 2 из них погасли. Сколько свечей погасло? Вы заходите в темную комнату. У вас есть керосиновая и газовая лампы. Что вы вначале зажжете? Проверочная работа №6 По улице идут два сына и два отца. Всего три человека. Может ли так быть? У отца шесть сыновей. Каждый сын имеет одну сестру. Сколько всего детей у этого отца? Две мухи соревнуются в беге. Первая муха бежит вверх и вниз по стене с одинаковой скоростью. Вторая бежит вниз вдвое быстрее, чем первая, а вверх – вдвое медленнее, чем первая. Которая из мух победит если: а) мухи бегут от пола до потолку и обратно; б) мухи бегут от потолка к полу и обратно? Проверочная работа №7 За сутки до дождя Петин кот всегда чихает. Сегодня кот чихнул «Завтра будет дождь», - подумал Петя. Прав ли он? До царя дошла весть, кто-то из трех богатырей убил Змея Горыныча. Приказал царь им явиться ко двору. Молвили богатыря: Илья Муромец: - Змея убил Добрыня Никитич. Добрыня Никитич: - Змея убил Алеша Попович. Алеша Попович: - Я убил Змея. Известно, что только один богатырь сказал правду, а двое слукавили. Кто убил Змея? Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли были тех же трех цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бима были зеленого, а рубашка нет. Каких цветов были туфли и рубашка у Бома и Бима? Проверочная работа №8 1. На первом месте по величине из змей находится анаконда или индийский питон, на втором месте — королевский питон, а на третьем месте — анаконда. Какая змея занимает какое место по величине, если известно, что ни одно из высказываний не является истинным? 2. Пять друзей — Дима, Саша, Коля, Сережа, Юра — решили купить себе удочки. Удочки были пяти цветов: красного, синего, белого, зеленого и черного. Известно, что: 1) Дима любит красный и синий цвета; 2) Сереже нравились синяя и зеленая удочки; 3) Коля купил зеленую удочку; 4) Юра отдал предпочтение красной, синей и черной удочкам. Кто какую удочку купил, если у всех были удочки разного цвета? 3. Катя, Володя, Лена делали к празднику украшения: гирлянды, звездочки, флажки. Катя не делала звездочки, Лена не делала звездочки и гирлянды. Все вырезали из бумаги разного цвета: желтого, красного, оранжевого. Флажки были красного цвета. Катя вырезала из оранжевой бумаги. Какие украшения и какого цвета делали Катя, Володя, Лена? Проверочная работа №9 Составить новое слово из первых слогов данных слов: - колос, рота, ваза - молоко, нерест, таракан - кора, лото, боксер - баран, рана, банщик - монета, лошадь, корова Найти «спрятанное» слово (соединяя слоги): - обруч, кара; - мука, рагу, диван Лягушка любит квакать Перед дождем Цапля слышит перед Дождем лягушку Любит цапля пенье Лягушки перед Едой А вот перевод этого стишка на язык племени Ням-ням: Ам ту му ям то Гу ля ям то ту Ля бу ту ам Ши ям Составьте фрагмент русско-нямнямского словаря. Проверочная работа №9 Как, имея два сосуда емкостью 5 и 8 литров, набрать из водопроводного крана 3 литра воды? Две хозяйки купили 8 литров молока. У одной 5 литров в 6-литровом бидоне, у другой – 3 литра в 5-литровом бидоне. Они решили разделить все молоко поровну, по 4 литра, пользуясь еще одним 2-литровым бидоном. Как это сделать? В бочке хранится несколько ведер бензина. Как из нее отлить 6 литров бензина в другую бочку с помощью 9-литрового и 5-литрового бидонов? Проверочная работа №10 Какие двузначные коды можно составить, используя только цифры 3 и 7? Код на замке чемодана состоит из четырех цифр. Его хозяин решил набрать четыре идущие подряд цифры, расположив их по порядку от меньшей к большей. Сколько существует вариантов такого рода? Сколько четных трехзначных чисел можно составить, используя только цифры 5 и 6? Проверочная работа №11 Шифр для сейфа составляется из трех разных цифр. Запишите все шифры, которые можно составить, используя цифры 1, 2 и 3. В костюмерной имеются желтые и белые кофты, а также синие, красные и черные юбки. Сколько из них можно составить различных костюмов? Оля, Костя, Нина, Таня и Галя должны по очереди дежурить в классе, и им нужно составить расписание. Оля вызвалась дежурить первой, а Галя сказала, что будет дежурить последней. Сколько вариантов расписания при этих условиях они могут составить? Проверочная работа №12 Саша выбрал в библиотеке пять книг, но одновременно можно взять только две книги. Сколько вариантов выбора двух книг из пяти есть у Саши? В школьной лотерее должно быть всего десять различных выигрышей. Есть ручки, блокноты, записные книжки, альбомы для рисования. Можно ли из этих предметов составить десять различных выигрышей, по два разных предмета в каждом? Проверочная работа №13 Какое наибольшее число точек попарных пересечений могут иметь три прямые? Какое наибольшее число точек попарных пересечений могут иметь четыре прямые? На сколько частей разбивают плоскость две пересекающиеся прямые? На сколько частей разбивают плоскость три прямые, пересекающиеся в одной точке? На сколько частей разбивают плоскость три попарно пересекающиеся прямые, не пересекающиеся в одной точке? 6 класс Примерные тексты задач, решаемых по теме «Логические задачи» 1. 5 школьников приехали из 5 различных городов в Архангельск на областную математическую олимпиаду. «Откуда вы, ребята?»- спросили их хозяева. Вот что ответил каждый из них. Андреев: «Я приехал из Онеги, а Григорьев живет в Каргополе». Борисов: «В Каргополе живет Васильев. Я же прибыл из Коряжмы». Васильев: «Я приехал из Онеги, а Борисов - из Котласа». Григорьев: «Я прибыл из Каргополя , а Данилов из Вельска». Данилов: «Да, я действительно из Вельска. Андреев же живет в Коряжме». Хозяева очень удивились противоречивости ответов приехавших гостей. Ребята объяснили им, что каждый из них высказал одно утверждение правильное, а другое ложное. Но по их ответам вполне можно установить, кто откуда приехал. Откуда приехал каждый школьник? 2. Пришел Иван-царевич в подземелье к Кощею Бессмертному Василису прекрасную освобождать. В подземелье три темницы. В одной из них томится Василиса, в другой расположился Змей Горыныч, а третья темница – пустая. На дверях есть надписи, но все они ложные. На первой темнице написано: «Здесь Василиса Прекрасная»; на второй темнице: «Темница №3 не пустая»; на третьей темнице написано «Здесь Змей Горыныч». В какой же темнице Василиса? Алеша Попович и Добрыня Никитич по очереди воюют с девятиглавым змеем. Они по очереди входят в пещеру и отрубают 1, 2 или 3 головы. Как начинающему бой Алеше обрести славу победителя (т. е. отрубить последнюю голову)? 3. В куче лежат 50 камней. Двое по очереди добавляют в нее любое число камней от 1 до 10. Выигрывает тот, кто первым сумеет довести количество камней до 100. Кто это будет – первый или второй? Сколько ходов потребуется победителю? 4. Имеется семь одинаковых по виду монет, одна из которых фальшивая, легче других. Требуется определить фальшивую монету. Какое минимальное число взвешиваний требуется? 5. Имеется восемь одинаковых по виду монет, одна из которых фальшивая, легче других. Требуется определить фальшивую монету. Какое минимальное число взвешиваний требуется? 6. На столе в ряд стоят шесть стаканов, первые три с напитком, а потом три пустых. Требуется расположить их так, чтобы стаканы с напитком и пустые стаканы чередовались через один, причем разрешается брать в руки только один стакан. 7. Из бочки, содержащей не менее 10л бензина, отлейте ровно 6л, используя бидон вместимостью 5л и девятилитровое ведро. 8. Некто имеет 12 пинт меда и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 пинт. У него два сосуда: один вместимостью в 8 пинт, а другой – вместимостью в 5 пинт. Каким образом налить 6 пинт меда в сосуд на 8 пинт? Какое наименьшее число переливаний необходимо при этом сделать? 9. Как при помощи чашечных весов и гири 200 г разделить 9 кг сахара на два пакета весом 2 кг и 7кг, если разрешается взвешивать не более трех раз? 10. В ящике содержится 24 кг гвоздей. Как на чашечных весах без гирь отвесить ровно 21 кг гвоздей? 11. В вашем распоряжении имеются четыре емкости – на 200 г, 400 г, 600 г, 800 г молока – все цилиндрической формы. Емкость, вмещающая 400 г, наполнена молоком, остальные пустые. Пользуясь только этими емкостями, разлейте молоко так, чтобы в каждой емкости-цилиндре оказалось ровно по 100 г молока. Проверочная работа по теме: «Задачи на переправы» Два солдата подошли к реке, по которой на лодке катаются двое мальчиков. Как солдатам переправиться на другой берег, если лодка вмещает только одного солдата, либо двух мальчиков, а солдата и мальчика уже не вмещает? Двум англичанам, путешествующим в дебрях Амазонки, и двум их проводникам из местного племени требуется переправиться на противоположный берег реки. В расположении путешественников имеется небольшая надувная лодка, способная вместить только двух человек. Англичане подозревают, что их проводники из племени людоедов, и чувствуют себя в безопасности только тогда, когда находятся вдвоем. Как устроить безопасную переправу? Дело было в Америке. Как-то раз подошли к реке англичанин, негр и индеец, каждый со своей женой. Всем нужно было переправиться на другой берег. В их распоряжении была только одна лодка (да и та без гребца), способная вместить лишь двоих. Договорившись между собой, мужчины решили было приступить к переправе, как вдруг выяснилось, что ни одна из жен не желает переправляться в лодке с чужим мужем или оставаться на берегу в мужском обществе без своего мужа. Мужья призадумались, но все же сумели догадаться, как выполнить желание своих жен. Как они сумели переправиться через реку? Самостоятельная работа по теме: «Задачи на взвешивания, переливания и переправы»
Проверочная работа по теме: «Выигрышные и проигрышные позиции» Алеша Попович и Добрыня Никитич воюют с девятиглавым змеем. По очереди богатыри ходят к его пещере и отрубают 1, 2 или 3 головы. Как начавшему бой Алеше обрести славу победителя змея (т.е. отрубить последнюю голову)? А если змей двенадцатиглавый? Двое играют в такую игру: первый называет однозначное число (то ест целое число от 1 до 9 включительно), второй прибавляет к нему еще какое-нибудь однозначное число и называет сумму, к этой сумме первый прибавляет еще какое-нибудь однозначное число и опять называет сумму и так далее. Выигрывает тот, кто первым назовет число 66. Как нужно играть в такую игру, чтобы выиграть? Кто выигрывает пари при правильной игре: начинающий или его партнер? Примерные тексты задач, решаемых по теме «Комбинаторика» 1. В тарелке лежало 5 яблок и 6 груш. Сколько вариантов выбора одного плода? 2. В магазине 2 разных конверта и 3 разные марки. Сколькими способами можно выбрать пару предметов: конверт и марку? 3. Сколько существует вариантов покупки одной розы, если продаются 3 алые, 2 белые и 4 желтые розы? 4. В столовой 4 первых блюда, 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать? 5. В вазе лежат 7 яблок, 3 груши и 4 апельсина. а) Сколькими способами можно взять из тарелки один плод? б) Сколькими способами можно взять из тарелки: (яблоко с грушей), (грушу и апельсин), (яблоко с апельсином)? в) Сколькими способами можно взять из тарелки два фрукта с разными названиями? 6. Сколько различных двузначных чисел можно составить используя цифры 1, 4 и 7, если цифры могут повторяться? 7. В пакетике драже лежат 9 красных, 10 синих и 12 зеленых конфет. а) Сколькими способами можно взять одну конфету? б) Сколькими способами можно взять из тарелки: красную и синюю конфету, красную и зеленую конфету, синюю и зеленую конфеты? в) Сколькими способами можно взять из пакетика две конфеты разного цвета? 8. Сколько существует трехзначных чисел, у которых все цифры четные 9. Сколько различных трехзначных чисел, меньших 400, можно составить из нечетных цифр, если любая из этих цифр может использоваться только один раз? 10. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материя шести цветов? 11. В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 различных уроков? 12. Телефонная станция обслуживает абонентов, у которых номера телефонов состоят из 7 цифр и начинаются с 394. На сколько номеров рассчитана эта станция? 13. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно? 14. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подарили на память друг другу свои фотографии. Причем каждый мальчик подарил каждому по одной фотографии. Сколько всего фотографий было подарено? 15. Антон, Борис, Василий купили 3 билета на футбольный матч на 1, 2 и 3-е места первого ряда. Сколькими способами они могут занять имеющиеся три места? Перечислите все способы. 16. В меню столовой предложены на выбор 3 первых, 5 вторых и 4 третьих блюда. Сколько различных вариантов обедов, состоящих из одного первого, одного второго и одного третьего блюда, можно составить из предложенного меню? 17. Маше на день рождения подарили три букета цветов: из роз (р), астр (а) и гвоздик (г). В доме было две вазы: хрустальная (х) и керамическая (к). Маша пробовала устанавливать каждый букет в каждую вазу. Перечислить все полученные сочетания букета с вазой. 18. Перечислить все возможные цветовые сочетания брюк, свитера и ботинок, если в гардеробе имеются брюки трех цветов: серые (с), бежевые (б) и зеленые (з); свитера двух расцветок: песочный (п) и малиновый (м); ботинки двух цветов: черные (ч) и коричневые (к). Самостоятельная работа по теме: «Комбинаторика»
Примерные тексты задач, решаемых по теме «Множества» 1. Запишите с помощью перечисления элементов множества: а) однозначных чисел; б) двузначных чисел, оканчивающихся цифрой 7; в) натуральных чисел, заключенных между числами 31 и 34. Придумайте свои множества. 2. Запишите, используя знаки принадлежности, следующие высказывания: а) число 15 принадлежит множеству натуральных чисел; б) число 243 – натуральное; в) число 54,56 не принадлежит множеству натуральных чисел; г) число ½ не является натуральным. 3. Определите, по какому признаку составлены множества: а) Х = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}; б) А = {17, 34, 51, 68, 85}; в) В = {17, 27, 37, 47, 57, 67, 77, 87, 97}; г) С = {13, 23, 43, 53, 73, 83}. 4. Задайте множества характеристическим свойством, обозначив произвольный элемент множества х: а) А = {1, 2, 3, 4, 5, 6, 7, 8, 9}; б) С – натуральные числа, большие 100; в) Е – множество нечетных чисел. 5. Каждый ученик класса изучает или английский, или испанский, или оба языка. Английский изучают 25 человек, испанский 27 человек, и английский и испанский – 18 человек. Сколько учеников в классе? 6. В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 – в шахматы. Сколько учащихся играют и в шашки и в шахматы? 7. В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их пересечении? объединении? 8. В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит мороженое? 9. В классе 35 учеников. Из них: 20 школьников занимаются в математическом кружке, 11 – в экологическом, 10 ребят не посещают эти кружки. Сколько экологов увлекаются математикой? 10. Из 40 учащихся класса 32 выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты? 11. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе – 12, причем отличников-спортсменов, увлекающихся лыжами, - 10? 12. В классе 36 учеников. Многие из них посещают кружки: физический (14 человек), математический (18 человек), химический (10 человек). Кроме того, известно, что 2 человека посещают все три кружка; из тех, кто посещает два кружка, 8 человек занимаются в математическом и физическом кружках, 5 – в математическом и химическом, 3 – в физическом и химическом. Сколько человек не посещают никаких кружков? Самостоятельная работа №1 по теме «Множества»
Самостоятельная работа № 2 по теме «Множества»
Для каждого из событий (1 - 4) определите, каким оно является: невозможным, достоверным или случайным: 1. Из списка журнала V класса (в котором есть и девочки, и мальчики) случайным образом выбран один ученик: 1) это мальчик; 2) выбранному ученику 11 лет; 3) выбранному ученику 11 месяцев; 4) этому ученику больше двух лет. 2. Сегодня в Сочи барометр показывает нормальное атмосферное давление. При этом: 1) вода в кастрюле закипела при t = 80 °С; 2) когда температура упала до - 5 °С, вода в луже замерзла. 3. Измерены длины сторон треугольника. Оказалось, что длина каждой стороны меньше суммы длин двух других сторон. 4. Бросают две игральные кости: 1) на первой кости выпало 3 очка, а на второй — 5 очков; 2) сумма выпавших на двух костях очков равна 1; 3) сумма выпавших на двух костях очков равна 13; 4) на обеих костях выпало по 3 очка; 5) сумма очков на двух костях меньше 15. В упражнениях 5—6 среди данных пар событий указать, какие являются совместными, а какие — несовместными. 5. В сыгранной Катей и Славой партии в шахматы: 1) Катя выиграла; Слава проиграл; 2) Катя проиграла; Слава проиграл. 6. Брошена игральная кость. На верхней грани оказалось: 1) 6 очков; 5 очков; 2) 6 очков; четное число очков. 7. Из событий: 1) «идет дождь»; 2) «на небе нет ни облачка»; 3) «наступило лето» — составить всевозможные па ры и выявить среди них пары совместных и пары несовместных событий. 8. Из событий: 1) «наступило утро»; 2) «сегодня по расписанию 6 уроков»; 3) «сегодня первое января»; 4) «температура воздуха в Салехарде + 20 °С» — составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий. 9. Имеется правильная треугольная пирамида — тетраэдр. Одна из ее граней серая, а 3 другие белые. Тетраэдр бросают на стол и наблюдают за гранью, которой он соприкасается со столом. Являются ли равновозможными события «тетраэдр упал на серую грань» и «тетраэдр упал на белую грань»? 10. Бросается игральный кубик, у которого: 1) 2 грани; 2) 3 грани окрашены в красный цвет, а остальные — в желтый. Являются ли равновозможными события «выпала желтая грань» и «выпала красная грань»? 11. Случайным образом выбрали двузначное число. Найдите вероятность того, что оно: а) оканчивается нулем; б) состоит из одинаковых цифр; в) больше 27 и меньше 46; г) не является квадратом целого числа. 12. Двузначное число составили из цифр 0, 1,2, 3, 4. Какова вероятность того, что это число: а) четное; в) делится на 5; б) нечетное; г) делится на 4? 13. Из четырех тузов случайным образом поочередно вытащили две карты. Найдите вероятность того, что: а) обе карты — тузы черной масти; б) вторая карта — пиковый туз; в) первая карта — туз красной масти; г) среди выбранных карт есть бубновый туз. Из четырех тузов случайным образом одновременно вытащили две карты. 14. Найдите вероятность того, что: а) обе карты — тузы черной масти; б) среди выбранных карт есть пиковый туз; в) среди выбранных карт есть туз красной масти; г) среди выбранных карт нет бубнового туза. 15. В коробке «Ассорти» — 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова вероятность того, что: а) обе конфеты окажутся с любимой Таниной начинкой — шоколадной; б) обе конфеты — с фруктовой начинкой; в) конфеты — с разными начинками? г) чему равна сумма вероятностей в пунктах а), б), в)? 16. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что: а) обе они согласные; б) среди них есть «ъ»; в) среди них нет «ъ»; г) одна буква гласная, а другая согласная. Самостоятельная работа по теме «Вероятность события»
|
