1.10 - Маятник Максвелла. Учебнометодическое пособие к лабораторной работе 10 Составители Полищук Виталий Ефремович Полищук Раиса Федоровна
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Маятник Максвелла Учебно-методическое пособие к лабораторной работе № 3. 10 Составители Полищук Виталий Ефремович Полищук Раиса Федоровна Целью работы является изучение законов динамики вращательного движения твердого тела, ознакомление с маятником Максвелла и методикой измерения на нем момента инерции колеса маятника Максвелла относительно оси, проходящей через его центр масс, а так же экспериментальное нахождение ускорения поступательного движения центра масс колеса маятника Максвелла. 1. Основные понятия вращательного движения твердого тела. Под твердым телом в механике понимается модель абсолютно твердого тела – тела, деформациями которого в условиях данной задачи можно пренебречь. Такое тело можно рассматривать как систему жестко закрепленных материальных точек. Любое сложное движение твердого тела всегда можно разложить на два основных вида движения – поступательное и вращательное. 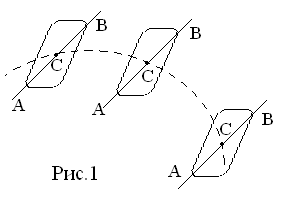 Поступательнымдвижением твердого тела называется движение, при котором любая прямая, проведенная через любые две точки тела, остается параллельной самой себе во все время (рис.1). При таком движении все точки твердого тела движутся совершенно одинаково, то есть имеют одну и ту же скорость, ускорение, траектории движения, совершают одинаковые перемещения и проходят одинаковый путь. Следовательно, поступательное движение твердого тела можно рассматривать как движение материальной точки. Такой точкой может являться, в частности, центр масс (центр инерции) тела С. Под центром масс тела понимается точка приложения результирующей массовых сил, действующих на тело. Массовые силы – это силы, пропорциональные массам элементов тела, на которые эти силы действуют, при условии что силы, действующие на все элементы тела, параллельны друг другу. Поступательнымдвижением твердого тела называется движение, при котором любая прямая, проведенная через любые две точки тела, остается параллельной самой себе во все время (рис.1). При таком движении все точки твердого тела движутся совершенно одинаково, то есть имеют одну и ту же скорость, ускорение, траектории движения, совершают одинаковые перемещения и проходят одинаковый путь. Следовательно, поступательное движение твердого тела можно рассматривать как движение материальной точки. Такой точкой может являться, в частности, центр масс (центр инерции) тела С. Под центром масс тела понимается точка приложения результирующей массовых сил, действующих на тело. Массовые силы – это силы, пропорциональные массам элементов тела, на которые эти силы действуют, при условии что силы, действующие на все элементы тела, параллельны друг другу. Так как при поступательном движении все элементарные массы Δmi твердого тела движутся с одинаковыми скоростями и ускорениями, то для каждой из них справедлив второй закон Ньютона: 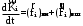 , ( 1) , ( 1)где 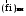 - сумма всех внутренних сил, действующих на элементарную массу Δmi (всего таких сил будет i-1, так как сама на себя частица действовать не может), а - сумма всех внутренних сил, действующих на элементарную массу Δmi (всего таких сил будет i-1, так как сама на себя частица действовать не может), а 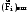 сумма всех внешних сил действующих на элементарную массу Δmi со стороны других тел. Просуммировав уравнения ( 1) по всему телу и учитывая, что сумма всех внутренних сил сумма всех внешних сил действующих на элементарную массу Δmi со стороны других тел. Просуммировав уравнения ( 1) по всему телу и учитывая, что сумма всех внутренних сил 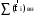 согласно третьему закону Ньютона равна нулю, получим закон динамики поступательного движения твердого тела: согласно третьему закону Ньютона равна нулю, получим закон динамики поступательного движения твердого тела: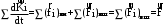 . (2) . (2) Или 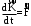 , (3) , (3)где 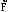 - результирующая всех внешних сил, действующих на тело в целом, - результирующая всех внешних сил, действующих на тело в целом, 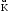 - импульс (количество движения) тела. Полученное уравнение (3) поступательного движения твердого тела совпадает с уравнением динамики материальной точки. - импульс (количество движения) тела. Полученное уравнение (3) поступательного движения твердого тела совпадает с уравнением динамики материальной точки.Вращательным движением твердого тела называется движение, при котором все точки тела описывают окружности, центры которых лежат на одной и той же прямой, называемой осью вращения тела. При вращательном движении все точки тела движутся с одной и той же угловой скоростью и угловым ускорением и совершают одинаковые угловые перемещения. Однако, как показывает опыт, при вращательном движении твердого тела вокруг закрепленной оси масса уже не является мерой его инертности, а сила – недостаточна для характеристики внешнего воздействия. Так же из опыта следует, что ускорение при вращательном движении зависит не только от массы тела, но и от ее распределения относительно оси вращения; зависит не только от силы, но и от точки ее приложения и направления действия. Поэтому, для описания вращательного движения твердого тела введены новые характеристики, такие как момент силы, момент импульса и момент инерции тела. При этом, следует иметь в виду, что существует два разных понятия этих величин: относительно оси и относительно любой точки О (полюса, начала), взятой на этой оси. Моментом силы 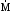 относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора 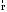 , проведённого из точки О в точку приложения результирующей силы , проведённого из точки О в точку приложения результирующей силы 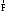 , на вектор этой силы: , на вектор этой силы:  (4) (4)В 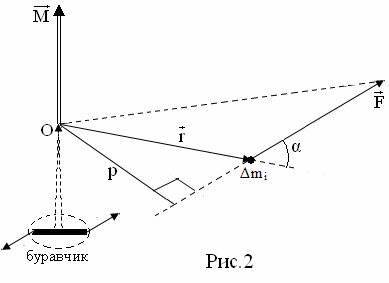 ектор момента силы 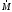 всегда перпендикулярен плоскости, в которой расположены вектора всегда перпендикулярен плоскости, в которой расположены вектора 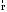 и и 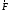 , а его направление относительно этой плоскости определяется по правилу векторного произведения или по правилу буравчика. Согласно правилу буравчика: если рукоятку буравчика вращать по направлению действия силы , а его направление относительно этой плоскости определяется по правилу векторного произведения или по правилу буравчика. Согласно правилу буравчика: если рукоятку буравчика вращать по направлению действия силы 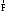 , то поступательное движение буравчика будет совпадать с направлением вектора момента силы , то поступательное движение буравчика будет совпадать с направлением вектора момента силы 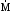 (рис.2). Вектора, направление которых связывают с направлением вращения (угловая скорость, угловое ускорение, момент силы, момент импульса и т.п.), называют псевдовекторамиили аксиальными в отличие от обычных векторов (скорость, радиус-вектор, ускорение и т.п.), которые называют полярными. (рис.2). Вектора, направление которых связывают с направлением вращения (угловая скорость, угловое ускорение, момент силы, момент импульса и т.п.), называют псевдовекторамиили аксиальными в отличие от обычных векторов (скорость, радиус-вектор, ускорение и т.п.), которые называют полярными.Величина вектора момента силы (численное значение момента силы) определяется согласно формуле векторного произведения (4), т.е. 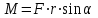 , где a - , где a - 4 угол между направлениями векторов 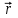 и и 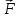 . Величина p= r·Sinα называется плечом силы (рис.2). Плечо силы р - это кратчайшее расстояние от точки О до линии действия силы . Величина p= r·Sinα называется плечом силы (рис.2). Плечо силы р - это кратчайшее расстояние от точки О до линии действия силы 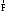 . .Моментом силы относительно оси, называется проекция на эту ось вектора момента силы, найденного относительно любой точки, принадлежащей этой оси. Ясно, что относительно оси момент силы является скалярной величиной. В системе СИ момент силы измеряется в Н·м. Для введения понятия момента импульса тела, введем сначала это понятие для материальной точки, принадлежащей вращающемуся твердому телу. Моментом импульса 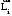 материальной точки Δmi относительно неподвижной точки О называется векторное произведение радиус-вектора материальной точки Δmi относительно неподвижной точки О называется векторное произведение радиус-вектора 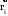 , проведенного из точки О в точку Δmi, на вектор импульса этой материальной точки: , проведенного из точки О в точку Δmi, на вектор импульса этой материальной точки: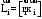 , (5) , (5)где 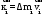 - импульс материальной точки. - импульс материальной точки.Моментом импульса твердого тела (или механической системы) относительно неподвижной точки О называется вектор 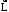 , равный геометрической сумме моментов импульса относительно этой же точки О всех материальных точек данного тела, т.е. , равный геометрической сумме моментов импульса относительно этой же точки О всех материальных точек данного тела, т.е. 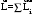 . .Моментом импульса твердого тела относительно оси называется проекция на эту ось вектора момента импульса тела 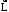 относительно любой точки, выбранной на данной оси. Совершенно очевидно, в этом случае момент импульса является скалярной величиной. В системе СИ момент импульса измеряется в относительно любой точки, выбранной на данной оси. Совершенно очевидно, в этом случае момент импульса является скалярной величиной. В системе СИ момент импульса измеряется в 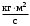 Мерой инертности тел при поступательном движении является их масса. Инертность же тел при вращательном движении зависит не только от массы тела, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности тела при вращательном движении является момент инерции тела I относительно оси вращения или точки. Момент инерции, как и масса, величина скалярная. Моментом инерции тела относительно оси вращения называется физическая величина равная сумме произведений масс материальных точек, на которые можно разбить все тело, на квадраты расстояний каждой из них до оси вращения: 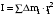 , (6) , (6)где 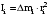 -момент инерции материальной точки. -момент инерции материальной точки.Моментом инерции тела относительно точки О, лежащей на оси, называется скалярная величина, равная сумме произведений массы каждой материальной точки данного тела на квадрат ее расстояния до точки О. Расчетная формула момента инерции аналогична формуле (6). В системе СИ момент инерции измеряется в кг·м2 . 2. Основной закон динамики вращательного движения твердого тела. Найдем связь между моментом силы и моментом импульса твердого тела, вращающегося вокруг неподвижной оси ОО. Для этого мысленно разобьем тело на элементарные части (массы), которые можно считать материальными точками. 5 Каждая из входящих в это твердое тело материальных точек будет двигаться по окружности в плоскости, перпендикулярной оси вращения, а центры всех этих окружностей будут лежать на этой оси. Понятно, что все точки тела в данный момент времени имеют одинаковую угловую скорость и одинаковое угловое ускорение. Рассмотрим i-материальную точку, масса которой Δmi, а радиус окружности, по которой она движется, ri. На нее действуют как внешние силы со стороны других тел, т 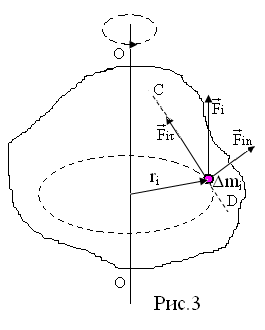 ак и внутренние - со стороны других материальных точек, принадлежащих этому же телу. Разложим результирующую силу ак и внутренние - со стороны других материальных точек, принадлежащих этому же телу. Разложим результирующую силу 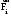 , действующую на материальную точку массы Δmi, на две взаимно перпендикулярные составляющие силы , действующую на материальную точку массы Δmi, на две взаимно перпендикулярные составляющие силы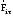 и и 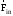 , причем так, чтобы вектор силы , причем так, чтобы вектор силы 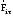 совпадал по направлению с касательной к траектории движения частицы, а сила совпадал по направлению с касательной к траектории движения частицы, а сила 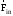 - перпендикулярна к этой касательной (Рис.3). Совершенно очевидно, что вращение данной материальной точки обусловлено только касательной составляющей силы - перпендикулярна к этой касательной (Рис.3). Совершенно очевидно, что вращение данной материальной точки обусловлено только касательной составляющей силы 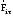 , величину которой можно представить в виде суммы внутренней , величину которой можно представить в виде суммы внутренней 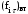 и внешней и внешней 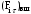 сил. В этом случае для точки Δmi второй закон Ньютона в скалярном виде будет иметь вид сил. В этом случае для точки Δmi второй закон Ньютона в скалярном виде будет иметь вид 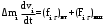  (7) (7)С учетом того, что при вращательном движении твердого тела вокруг оси, линейные скорости движения материальных точек по круговым траекториям различны по величине и направлению, а угловые скорости w для всех этих точек одинаковы (и по величине и направлению), заменим в уравнении (7) линейную скорость на угловую (vi=wri): 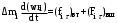 . (8) . (8)Введем в уравнение (8) момент силы, действующей на частицу. Для этого умножим левую и правую часть уравнения (8) на радиус ri, который по отношению к результирующей силе является плечом: 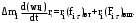 . (9) . (9)Или, 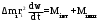 , (10) , (10)где каждый член в правой части уравнения (10) есть момент соответствующей силы относительно оси вращения. Если в это уравнение ввести угловое ускорение 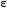 вращения материальной точки массы Δmi относительно оси ( вращения материальной точки массы Δmi относительно оси (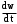 = =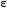 ) и ее момент инер- ) и ее момент инер-ции ΔIi относительно этой же оси ( 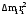 =ΔIi), то уравнение вращательного движе- =ΔIi), то уравнение вращательного движе-6 ния материальной точки относительно оси примет вид: ΔIi· 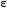 = =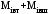 (11) (11)Аналогичные уравнения можно записать для всех других материальных точек, входящих в данное твердое тело. Найдем сумму этих уравнений с учетом того, что величина углового ускорения 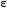 для всех материальных точек данного вращающегося тела будет одинаковой, получим: для всех материальных точек данного вращающегося тела будет одинаковой, получим: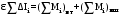 . (12) . (12)Суммарный момент внутренних сил 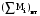 равен нулю, так как каждая внутренняя сила, согласно третьему закону Ньютона, имеет равную по величине, но противоположно направленную себе силу, приложенную к другой материальной точке тела, с таким же плечом. Суммарный момент равен нулю, так как каждая внутренняя сила, согласно третьему закону Ньютона, имеет равную по величине, но противоположно направленную себе силу, приложенную к другой материальной точке тела, с таким же плечом. Суммарный момент 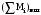 = М – есть вращающий момент всех внешних сил, действующих на вращающееся тело. Сумма моментов инерции = М – есть вращающий момент всех внешних сил, действующих на вращающееся тело. Сумма моментов инерции 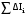 =I определяет момент инерции данного тела относительно оси вращения. После подстановки указанных величин в уравнение (12) окончательно получим: =I определяет момент инерции данного тела относительно оси вращения. После подстановки указанных величин в уравнение (12) окончательно получим: I I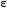 =M. (13) =M. (13)Уравнение (13) называется основным уравнением динамики вращательного движения твердого тела относительно оси. Так как 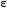 = =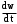 , а момент инерции тела относительно данной оси вращения является постоянной величиной и, следовательно, его можно внести под знак дифференциала, то уравнение (13) можно записать в виде: , а момент инерции тела относительно данной оси вращения является постоянной величиной и, следовательно, его можно внести под знак дифференциала, то уравнение (13) можно записать в виде: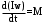 . (14) . (14)Величина Iw=L (15) называется моментом импульса тела относительно оси. C учетом (15) уравнение (14) можно записать в виде: 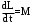 (16) (16) Уравнения (13-16) носят скалярный характер, и применяются только для описания вращательного движения тел относительно оси. При описании вращательного движения тел относительно точки (или полюса, или начала), принадлежащей данной оси, указанные уравнения соответственно записываются в векторном виде: 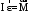 (13*); (13*); 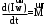 (14*); (14*);  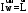 (15*); (15*); 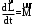 (16*). (16*).При сравнении уравнений поступательного и вращательного движения тела видно, что при вращательном движении вместо силы выступает ее момент силы, вместо массы тела – момент инерции тела, вместо импульса (или количества движения) – момент импульса (или момент количества движения). Из уравнений (16) и (16*) следует соответственно уравнение моментов относительно оси и относительно точки: dL=Mdt (17); 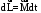 (17*) . (17*) .Согласно уравнению моментов относительно оси (17) – изменение момента импуль- 7 са тела относительно неподвижной оси равно моменту импульса внешней силы, действующей на тело относительно этой же оси. Относительно точки (17*) уравнение моментов формулируется: изменение вектора момента импульса относительно точки равно импульсу момента вектора силы, действующего на тело, относительно этой же точки. Из уравнений (17) и (17*) вытекает закон сохранения момента импульса твердого тела как относительно оси, так и относительно точки. Из уравнения (17) следует, если суммарный момент всех внешних сил М относительно оси равен нулю ( M=0, следовательно и dL=0) то момент импульса этого тела относительно оси его вращения остается постоянной величиной (L=Const). Относительно точки: если суммарный вектор момента всех внешних сил относительно точки вращения О остается неизменным, то вектор момента импульса этого тела относительно этой же точки О остается постоянным. Надо отметить, что если система отсчета, относительно которой рассматривается вращение тела, является неинерциальной, то момент силы М включает в себя как момент сил взаимодействия, так и момент сил инерции относительно той же оси или точки. 3. Описание установки. Вывод рабочей формулы. Рис.4. Лабораторная установка. О  снование 1, оснащено тремя регулировочными опорами, с помощью которых устанавливается вертикальное положение штативов 2 и 9. снование 1, оснащено тремя регулировочными опорами, с помощью которых устанавливается вертикальное положение штативов 2 и 9.С помощью миллиметровой линейки 3 и двух передвижных визиров 4 определяется расстояние пройденное центром маятника 5 при его падении. В верхней части штативов 2 расположен узел 6 для регулировки длины нитей маятника 5. На нижнем подвижном кронштейне 7 установлен «световой барьер» 8 – электронный измеритель времени. На стойке 9 расположено «пусковое устройство» 10. Основным элементом установки является маятник 5, состоящий из диска, через центр которого проходит ось диаметром D. На эту ось наматываются две симметрично расположенные относительно плоскости диска нити одинаковой длины. 8 Действие установки основано на законе сохранения механической анергии: полная механическая анергия Е системы, на которую действуют только консервативные силы, постоянна и определяется согласно уравнения: Е = 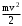 + + 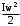 , (18) , (18)где 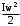 -кинетическая энергия вращательного движения маятника, I-момент инерции маятника, w-угловая скорость вращательного движения диска. -кинетическая энергия вращательного движения маятника, I-момент инерции маятника, w-угловая скорость вращательного движения диска.Закручивая на ось маятника нити, мы поднимаем его на высоту h и создаем ему запас потенциальной энергии. Если отпустить маятник то он начинает опускаться под действием силы тяжести, приобретая одновременно вращательное движение. В нижней точке, когда маятник опустится на полную длину нитей, поступательное движение вниз прекратится. При этом раскрутившийся диск со стержнем продолжает вращательное движение в том же направлении по инерции и снова наматывает нити на стержень. Вследствие этого диск со стержнем начинает подниматься вверх. После достижения наивысшей точки цикл колебательного движения возобновится. Диск со стержнем будет совершать колебания вверх и вниз, такое устройство и называется маятником Максвелла.. Для получения рабочей формулы рассмотрим силы, действующие на маятник Максвелла (рис.5). Т 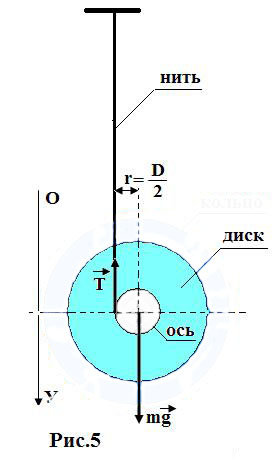 акими силами являются: сила тяжести m акими силами являются: сила тяжести m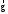 , приложенная к центру масс системы и сила натяжения нитей , приложенная к центру масс системы и сила натяжения нитей 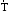 . Запишем для этой системы уравнение поступательного движения маятника. В соответствии со вторым законом Ньютона для поступательного движения центра массы маятника уравнение движения имеет вид: . Запишем для этой системы уравнение поступательного движения маятника. В соответствии со вторым законом Ньютона для поступательного движения центра массы маятника уравнение движения имеет вид:m 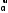 = m = m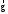 +2 +2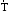 , где , где 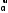 -ускорение центра масс маятника, -ускорение центра масс маятника, 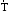 - сила натяжения одной нити. Спроектируем это уравнение на ось ОУ совпадающую с направлением движения центра масс маятника: - сила натяжения одной нити. Спроектируем это уравнение на ось ОУ совпадающую с направлением движения центра масс маятника: m  = mg – 2T (19) = mg – 2T (19)Помимо поступательного движения маятник участвует и во вращательном движении за счет действия на него момента силы Т. Тогда, для такого движения маятника запишем основной закон динамики вращательного движения как для абсолютно твердого тела: I 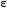 =М, (20) =М, (20)где I – момент инерции колеса маятника относительно его оси вращения, 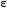 -угловое ускорение маятника, М – результирующий момент внешних сил относительно оси вращения колеса маятника. -угловое ускорение маятника, М – результирующий момент внешних сил относительно оси вращения колеса маятника.Если нет проскальзывания между осью и нитями и нить можно считать нерастяжимой, то линейное ускорение  связано с угловым связано с угловым 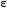 кинематическим соотноше- кинематическим соотноше-9 нием: 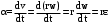 , где v- линейная скорость движения центра масс маятника, r- радиус оси маятника. Тогда угловое ускорение , где v- линейная скорость движения центра масс маятника, r- радиус оси маятника. Тогда угловое ускорение 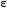 можно записать в виде можно записать в виде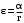 (21) (21)Так как сила тяжести m 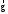 проходит через центр массы системы и, следовательно, ее момент силы равен нулю, то момент силы М, действующий на маятник, будет обусловлен действием только суммарной силы натяжения, равной 2Т. В этом случае, и с учетом уравнения (21), уравнение (20) можно записать в виде: проходит через центр массы системы и, следовательно, ее момент силы равен нулю, то момент силы М, действующий на маятник, будет обусловлен действием только суммарной силы натяжения, равной 2Т. В этом случае, и с учетом уравнения (21), уравнение (20) можно записать в виде: 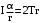 (22) (22)Из уравнения (19) найдем результирующую силу 2Т и подставим ее в уравнение (22): 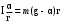 . (23) . (23)Разделив правую и левую часть уравнения (23) на величину ускорения  , после простых преобразований, получим формулу для расчета момента инерции I в виде: , после простых преобразований, получим формулу для расчета момента инерции I в виде: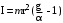 . (24) . (24)Так как величины I, m и r, входящие в уравнение (24), в процессе движения не изменяются, то движение маятника должно происходить с постоянным ускорением. Для такого движения расстояние h, пройденное за время t, при движении с нулевой начальной скоростью равно 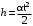 . Откуда . Откуда 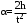 . Подставив найденное ускорение . Подставив найденное ускорение  в уравнение (24) и заменив величину радиуса оси маятника r на ее диаметр D, окончательно получим основную рабочую формулу для расчета момента инерции маятника: в уравнение (24) и заменив величину радиуса оси маятника r на ее диаметр D, окончательно получим основную рабочую формулу для расчета момента инерции маятника: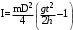 . (25) . (25)В рабочей формуле (25): m – масса маятника, равная сумме масс диска mд, и оси mо; D – внешний диаметр оси маятника вместе с намотанной на нее нитью подвески ( D = D0 + do, где Do – диаметр оси маятника, do – диаметр нити подвески); t - время прохождения маятником расстояния h при его падении; g – ускорение свободного падения. Порядок выполнение работы. Регулируя длину нитей регулировочными винтами 6, установите горизонтальное положение стержня (оси), на котором закреплено колесо маятника Максвелла. Установите световой барьер 8 так, чтобы при движении маятника Максвелла стержень (ось маятника) свободно проходил через световой барьер. Измерительной линейкой 3 определите расстояние h, на которое переместится при движении центр масс колеса Максвелла. Расположите пусковое устройство 10 так, чтобы его штырь в нажатом состоянии удерживал бы колесо маятника Максвелла от движения, а в отжатом состоянии обеспечивал бы свободное движение этого колеса. Приведите колесо в соприкосновение с нажатым штырем пускового устройства (рекомендуется положение штыря зафиксировать с помощью винта-стопора). Для этого медленно вращая стержень, плотно намотать на него обе нити, на которых подвешен маятник. Подключите световой барьер в сеть. Установите переключатель светового барьера в положение Нажмите на световом барьере кнопку сброса “Set”и приведите маятник Макс- велла в движение, отпустив штырь пускового устройства. Сразу же после этого вновь надавите на штырь пускового устройства и удерживайте его до тех пор, пока стержень не пересечет световой барьер. Датчик покажет время движения стержня t, а, следовательно, и маятника Максвелла до пересечения стержнем (осью) отметки на датчике светового барьера. Измерения 3-7 повторить для других положений датчика, задавая их путем его перемещения вдоль штативов 2 в области расстояний от 10 до 70 см ниже исходного положения маятника с интервалом в 10 см. Начальное (стартовое) положение маятника не изменяйте. Результаты измерений занести в таблицу. Штангенциркулем измерить диаметр стержня (оси) Do маятника Максвелла и толщину нити do. По данным таблицы: а) используя формулу (25) определить среднее значение момента инерции колеса маятника Максвелла, найти погрешность и относительную ошибку результата; б) по формуле 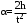 рассчитать среднее значение ускорения центра масс колеса маятника Максвелла, найти погрешность и относительную ошибку результата. рассчитать среднее значение ускорения центра масс колеса маятника Максвелла, найти погрешность и относительную ошибку результата.в) по данным таблицы hi и ti построить график зависимости расстояния, пройденного точкой центра масс колеса Максвелла при вертикальном движении вниз, от времени. .Таблица D=( Do + do ) = ……м
|
