инженергая графика. стандарты инженерной графики. Учебное пособие Для студентов направлений подготовки
 Скачать 3.24 Mb.
|
Р |
исунок 4 Шрифт чертёжный.  |
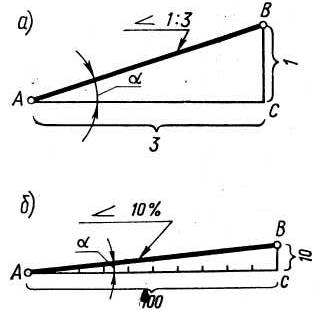| Рисунок.5(а. б) вычерчивание уклона |
При выполнении рабочих чертежей некоторых деталей (пробки кранов, клапаны и др.) чертят усеченный конус. На таких деталях необходимо указать конусность.
Конусностью К называется отношение диаметра основания прямого кругового конуса к его высоте: К= D/H(рис 6.) Для усеченного конуса конусность выражается отношением разности диаметров окружностей оснований к его высоте: К= (D-d)/h=2tg.. Нанесение размера конусности показано на рис.6, рис.7
 |
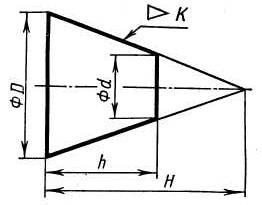| Рисунок. 6. Нанесение размеров конусности»1 |
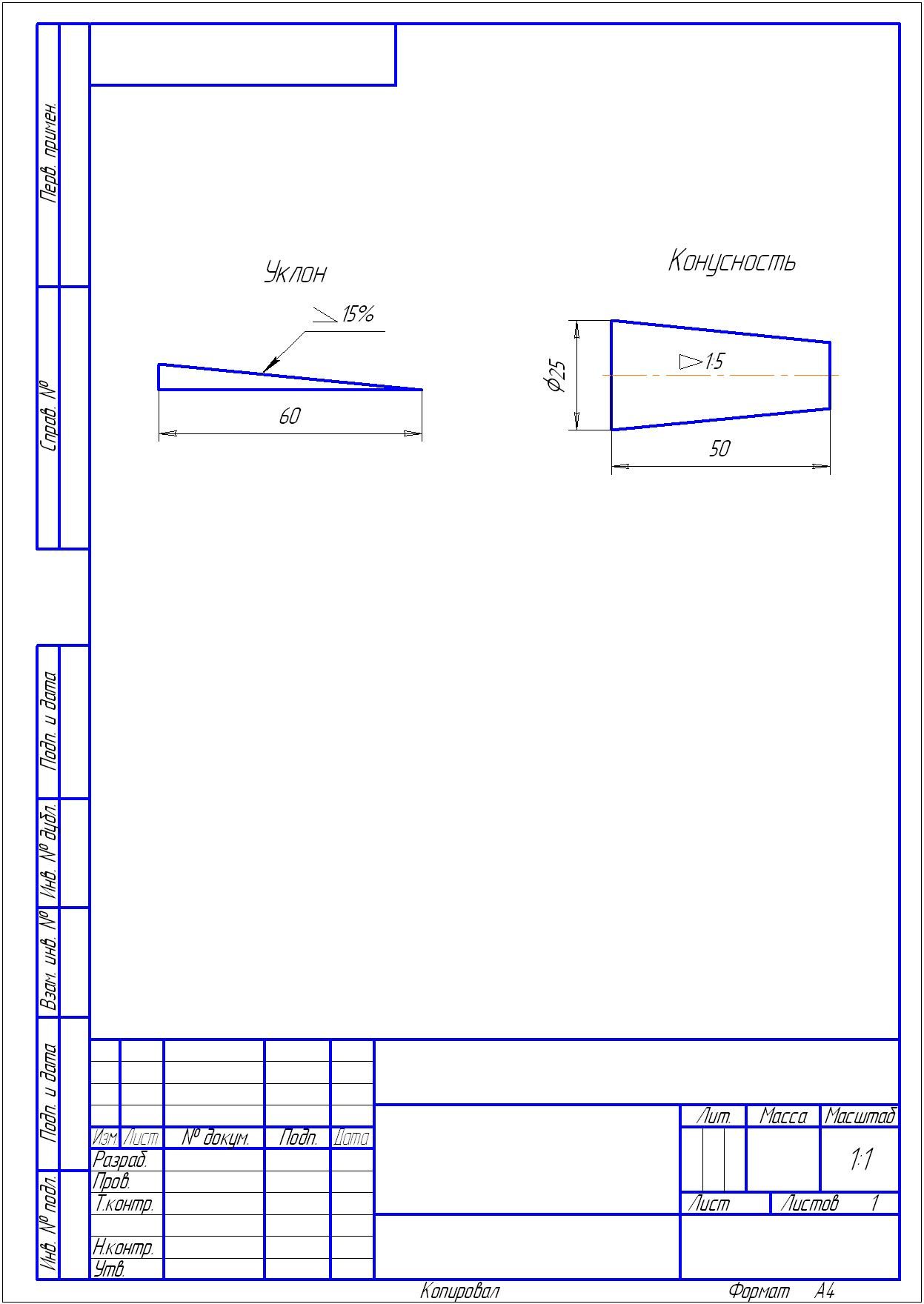
Рисунок 7 Образец выполнения чертежа уклона и конусности.
3. Сопряжения
«Сопряжением называется плавный переход одной линии (прямой или кривой) в другую кривую или прямую. Независимо от формы сопрягаемых линий (прямых или кривых) построение сопряжения дугой заданного радиуса выполняется по следующему плану.
Находят центр сопрягающей дуги окружности, который расположен в пересечении вспомогательных линий. Вспомогательные линии являются геометрическим местом точек, удаленных от заданных сопрягаемых линий на расстоянии R, равное радиусу сопряжения. (Все точки вспомогательных линий находятся на расстоянии R от заданной линий).
Определяют точки сопряжения (касания).
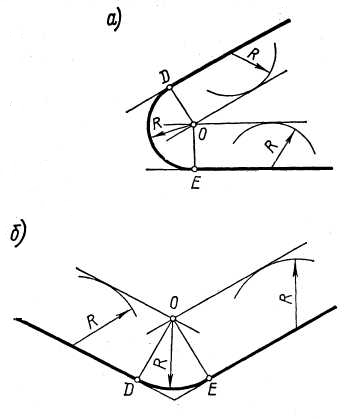
На рис. 8(а, б) приведены примеры построения сопряжений дугой заданного радиуса двух прямых, образующих острый и тупой углы.
|
Центр сопряжения О определяется как точка пересечения вспомогательных прямых, параллельных сопрягаемым прямым и проведенным на расстоянии Rот них. Перпендикуляры, опущенные из центра на сопрягаемые прямые, определяют точки сопряжения (касания) DиE.
|
На рис. 9 показано построение сопряжения дугой заданного радиуса R прямой с дугой окружности радиуса R1. Центром сопряжения О будет точка пересечения вспомогательной прямой, параллельной заданной и расположенной на расстоянии R, со вспомогательной дугой радиуса R1+ R, проведенной из центра О1. Точка сопряжения D , будет основанием перпендикуляра, опущенного из точки О на сопрягаемую прямую, а точка сопряжения Е получена в пересечении сопрягаемой дуги с линией, соединяющей центры О1 и О.
На рис. 10. а, дано построение сопряжений дугой заданного радиуса R двух дуг, проведенных из центров О1 и О2 радиусами R1 и R2.
Сопрягающая дуга касается данных окружностей внешней стороной.
Центр сопрягающей дуги О находится в точке пересечения окружностей радиусов R1 + Rи R2 + R. Точки сопряжения расположены на прямых, соединяющих центры.
На рис. 10. б, приведен случай, когда сопрягающая дуга радиуса R касается заданных окружностей внутренней стороной. Центр сопрягающей дуги О будет в пересечении дуг окружностей, радиусы которых равны разностям R - R1и R- R2.
 |  |
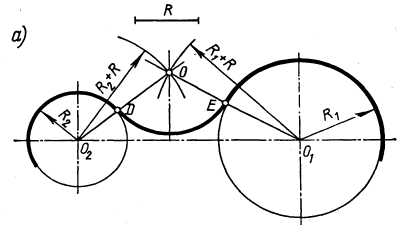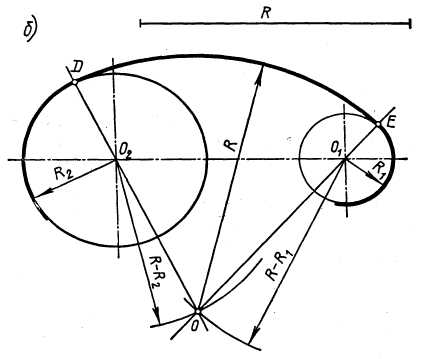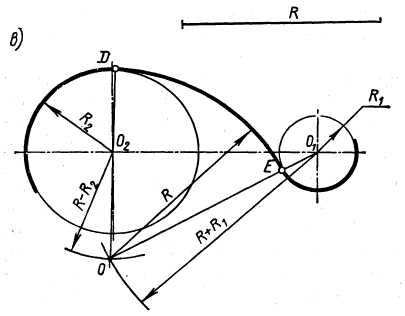 | Рисунок.10(а, б, в) а) построение внешнего сопряжения между двумя окружностями; б) построение внутреннего сопряжения между двумя окружностями; в) построение смешанного сопряжения между двумя окружностями. |
На рис.10. в показано сопряжение дугой радиуса R двух окружностей разных диаметров. При этом одной окружности сопрягающая дуга касается внешней стороной, а другой – внутренней. Центр сопряжения О в этом случае будет в точке пересечения окружностей радиусов R+ R1 и R- R2.»2