Медков В.М. Демография, учебное пособие. Учебное пособие. Серия Учебники и учебные пособия
 Скачать 2.69 Mb. Скачать 2.69 Mb.
|
6.5. ПОСТРОЕНИЕ ТАБЛИЦ СМЕРТНОСТИ6.5.1. Построение полной таблицы смертностиПостроение таблиц смертности является в принципе несложной, но достаточно трудоемкой вычислительной процедурой. Она включает в себя несколько этапов3:
Методы построения таблиц смертности занимают большое место в демографии. Можно повторить уже сказанное выше, что история демографии в значительной мере совпадает с историей разработки и совершенствования этих методов. Современные таблицы смертности рассчитываются с помощью т.н. косвенного, или демографического, метода. Демографический метод назван так потому, что в его основе лежат данные о повозрастной смертности, а также о возрастно-половой структуре населения, получаемые во время переписей и текущего учета. Косвенным этот метод назван, чтобы противопоставить его т.н. прямому методу, или, иначе, методу Р. Бека, основанному на непосредственном расчете показателей таблицы смертности в ситуации, когда известно распределение смертей на элементарные совокупности сетки Лексиса4. Исходным показателем здесь служит повозрастной коэффициент смертности, который приравнивается к табличному коэффициенту смертности (dx/Lx) и на основе которого определяются все функции таблицы смертности, начиная, разумеется, с вероятности умереть в возрасте х лет. Демографический метод позволяет строить таблицы смертности, наиболее адекватно отражающие ее уровень. При этом на величину итоговых показателей не влияют колебания чисел родившихся и умерших в годы, предшествовавшие расчету5. Проблема, связанная с переходом от повозрастных коэффициентов смертности к вероятностям смерти на возрастном интервале (х, х+п) лет, состоит в том, что первые, как известно, рассчитываются по отношению к общему числу человеко-лет, прожитых населением на этом возрастном интервале, или к его приближению, т.е. среднегодовому населению. Вторые же рассчитываются по отношению к численности населения в начале возрастного интервала. Чтобы построить таблицу смертности, надо установить соотношение между ними, т.е. между тхи qx. Иначе говоря, нужно перейти от тхк qx6. Пусть Nx- число доживающих до возраста х лет в реальном населении. Из этого числа до следующего возраста х+1 лет не доживет Dx. Тогда, по определению: Вместе с тем повозрастной коэффициент смертности тхравен отношению Dx к числу человеко-лет, прожитых Nx в течение интервала (х, х + 1). Это число человеко-лет, в свою очередь, равно сумме двух слагаемых: Первое слагаемое - это (Nx - Dx, т.е. число человеко-лет, прожитых на этом интервале возраста теми, кто дожил до возраста (х, х + 1). Второе слагаемое - это число человеко-лет, прожитых на этом интервале возраста теми, кто не дожил до возраста (х, х + 1), т.е. умер на этом интервале возраста. Это число равно a'x-Dx. 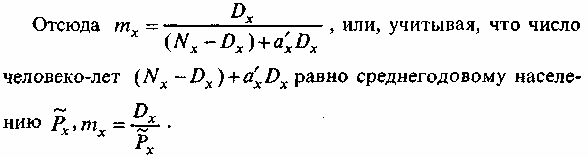 Последнее выражение есть знакомая формула расчета повозрастного коэффициента смертности. Решим уравнение Рх = (NX -Dx) + a'xDxотносительно Nx: Nx=Px+(1-a'xDx). Подставим это выражение в приведенную выше формулу для qx. Если числитель и знаменатель этого выражения разделить на Рx , то получим искомое базисное соотношение между qxи тх: 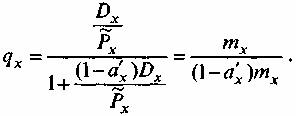 Величины а0 а1 ...варьируют от страны к стране в зависимости от уровня смертности. Для развивающихся стран, в которых смертность высока, обычно принимается а0 - 0,3, a1 - 0,4 и 0,5 для всех остальных. Там же, где смертность низка, наилучшей величиной для а0 является 0,1. В целом выбранная величина не является критичной, за исключением а0. Более того, существует альтернативный путь определения q0 без использования вышеприведенной формулы. Речь идет о простом приравнивании q0 к коэффициенту младенческой смертности. Newell С. Methods and Models in Demography. London. 1988. P. 69. Приведенное выше уравнение является фундаментальным для построения современных таблиц смертности. Зная все qxи выбрав корень таблицы смертностиl0 , можно, используя приведенные выше соотношения между ними, построить все остальные функции таблиц смертности. |
