Экзаменационные вопросы_Высш мат. Учебной дисциплины ен. 01. Элементы высшей математики по специальности 09. 02. 01 Компьютерные системы и комплексы Экзаменационные вопросы предназначены для контроля и оценки образовательных достижений обучающихся,
 Скачать 83.45 Kb. Скачать 83.45 Kb.
|
|
Экзаменационные вопросы учебной дисциплины ЕН.01. «Элементы высшей математики» по специальности 09.02.01 Компьютерные системы и комплексы Экзаменационные вопросы предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины Элементы высшей математики. Вопросы разработаны на основании положений: основной профессиональной образовательной программы по направлению подготовки специальности СПО 09.02.01 Компьютерные системы и комплексы; программы учебной дисциплины Элементы высшей математики. Вопросы: Матрицы, действия над матрицами. Определители 1-го, 2-го, 3-го порядков. Правило треугольников. Определители n-го порядка. Теорема Лапласа. Обратная матрица. Алгоритм нахождения обратной матрицы. Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных преобразований. Система линейных уравнений. Метод обратной матрицы. Формулы Крамера. Метод Гаусса. Векторы и операции над ними. Проекция вектора на ось и ее свойства. Декартова прямоугольная система координат. Полярная система координат. Скалярное, векторное и смешанное произведения векторов. Уравнения прямых. Угол между прямыми. Кривые второго порядка на плоскости: эллипс, парабола, гипербола. Предел функции в точке. Основные теоремы о пределах. Предел функции при x, стремящемся к бесконечности. Замечательные пределы. Число е. Непрерывность функции в точке и на промежутке. Точка непрерывности функции. Точка разрыва функции. Свойства непрерывных функций. Приращение аргумента. Приращение функции. Производная функции. Дифференциал функции. Геометрический смысл производной. Механический смысл производной. Таблица производных. Понятие сложной функции. Производная сложной функции. Схема исследования функции. Область определения функции. Множество значений функции. Четность и нечетность функции. Нули функции. Промежутки знакопостоянства функции. Возрастание и убывание функции, правило нахождения промежутков монотонности. Точки экстремума функции, правило нахождения экстремумов функции. Производные высших порядков. Физический смысл второй производной. Исследование функции с помощью второй производной. Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов. Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям. Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции). Основные свойства определенного интеграла. Геометрический смысл определенного интеграла. Методы вычисления определенных интегралов. Формула Ньютона-Лейбница. Геометрические и физические приложения определенного интеграла. Функции нескольких переменных. Частные производные. Понятие дифференциального уравнения. Общее и частное решение дифференциального уравнения. Интегральные кривые. Задача Коши. Задачи, приводящие к дифференциальным уравнениям. Методы решения дифференциальных уравнений. Понятие числового ряда. Сходимость и расходимость числовых рядов. Необходимый признак сходимости ряда. Признак сравнения. Признак Даламбера. Понятие знакочередующегося ряда. Признак сходимости Лейбница. Абсолютная и условная сходимость знакопеременного ряда. Функциональные ряды. Степенные ряды. Область сходимости степенного ряда. Разложение элементарных функций в ряд Маклорена. Экзаменационные задания Вычислить предел 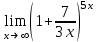 . .Вычислить пределы: а) 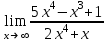 ; б) ; б) 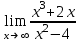 ; в) ; в) 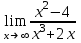 . .Вычислить предел 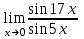 . .Вычислить предел 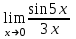 . .Вычислить предел 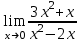 . .Вычислить предел 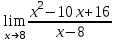 . .Исследовать функцию 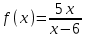 на непрерывность в точке на непрерывность в точке 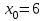 . .Исследовать функцию 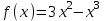 и построить ее график. и построить ее график.Вычислить значение производной следующих функций в точке 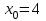 : :а) 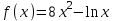 ; б) ; б) 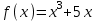 . .Найти производную функции 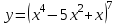 . .Найти производную функции 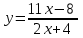 . .Найти производную функции 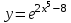 . .Найти производную функции 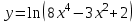 . .Найти неопределенный интеграл 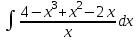 . .Найти неопределенный интеграл методом замены переменной 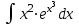 . .Найти неопределенный интеграл методом замены переменной 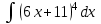 . .Найти неопределенный интеграл методом замены переменной 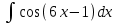 . .Найти неопределенный интеграл методом замены переменной 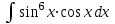 . .Вычислить определенный интеграл 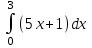 . .Вычислить определенный интеграл 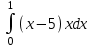 . .Вычислить определенный интеграл 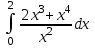 . .Скорость движения точки изменяется по закону 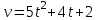 (м/с). Найти путь s, пройденный точкой за 4 с от начала движения. (м/с). Найти путь s, пройденный точкой за 4 с от начала движения.Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями 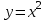 , , 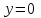 , , 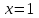 , , 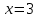 , вокруг оси Ox. , вокруг оси Ox.Вычислить площадь фигуры, ограниченной линиями 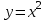 , , 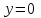 , , 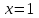 , , 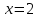 . .Решить дифференциальное уравнение 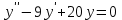 . .Решить задачу Коши: 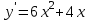 , , 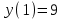 . .Решить дифференциальное уравнение 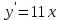 . .Даны векторы 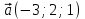 и и 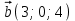 (для № 1-5). (для № 1-5).Найти 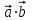 . .Найти 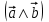 . .Найти 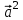 . .Найти 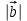 . .Найти координаты векторов 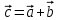 , , 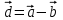 , , 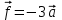 . .В прямоугольной декартовой системе координат построить точки A (0; 0), C (-3; 4), D (-2; 2) E (10; -3). Определить расстояние между точками C и D, A и D, D и E. Построить точки, заданные полярными координатами: A (4; 0), B (2; 3/2), C (3; ). Даны точки в прямоугольной системе координат A (0; 5), B (-3; 0),C ( 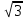 ; 1). Найти их полярные координаты. ; 1). Найти их полярные координаты.Составить уравнение плоскости проходящей через точки 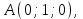 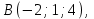 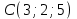 . .Определить, при каком  перпендикулярны прямые: перпендикулярны прямые: 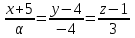 и и 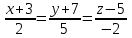 . .Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если действительная полуось 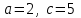 . .Составить уравнение плоскости, проходящей через точки 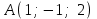 и и 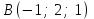 параллельно вектору параллельно вектору 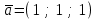 . .Уравнение прямой, проходящей через точки 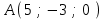 и и 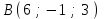 , может иметь вид… , может иметь вид…Найти эксцентриситет эллипса 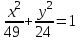 . . |
