|
|
Указатель на корень дерева Проверим дерево на существование и на наличие потомков. Создадим указатель и присвоим ему значение на ребенка узла, создадим счетчик
1 билет (Степень дерева)
Может быть два представления дерева общего вида
1.
Представление через бинарное дерево- каждый узел дерева имеет структурный тип item с полями
Child и brother – указатели на ребенка и брата соответственно. Задача сводится к тому чтоб найти узел с максимальным количеством братьев – родитель этого узла будет узлом с максимальной степенью.
Рассмотрим эту задачу:
Функция power для подсчета степени дерева, в функцию передаем указатель на корень дерева:
1.Проверим дерево на существование и на наличие потомков.
2.Создадим указатель и присвоим ему значение на ребенка узла, создадим счетчик
Будем считать количество братьев данного узла и прибавлять к счетчику степени узла 1.
Таким образом по посчитали степень для узла-родителя.
3.Затем спускаемся ниже по дереву к потомку (для которого мы в прошлом пункте посчитали количество братьев) и в цикле рекурсивно запускаем функция power для всех его братьев, и меняем значение максимальной степени, посчитанной в предыдущем пункте, если оно больше имеющегося.
4.Возвращаем посчитанное значение максимальной степени
Сложность O(n)
\\степень для двоичного
также задаем структуру двоичного дерева, проверяем на существование
так как в двоичном дереве максимальная степень будет равна 2, берем и проверяем наличие правого и левого потомка. Если у нас нет правого потомка, то уменьшаем cur_pow на 1, если левого, то тоже на один. Если cur_pow равен 2, то возвращаем cur_pow, т.к. это наибольшая возможная степень двоичного дерева. В конце возвращаем максимум из трёх возможных значений - степень левого узла, степень правого узла, степень текущего узла.
сложность О(n)
2.
Представление узла через массив указателей на детей.
Необходимо три структурных типа:
-тип узла дерева который хранит поле name-значение узла и поле children – очередь указателей
на детей узла.
-тип элемента массива
-тип самого массива(вектора)
Функция поиска в ширину, запускаем из корня:
Пусть текущий элемент-curr. Изначально curr равен первому элементу в массиве потомков корня.
Будем хранить обрабатываемые элементы в очереди. Помещаем в очередь всех потомков текущего корня(помещаем в очередь curr и меняем curr на curr->next).
Затем запускаем цикл while пока очередь не пуста: вытаскиваем из очереди первый элемент(т.е. первый потомок и сравниваем количество его потомков с максимальным, если оно больше, то приравниваем максимальное к нему.(изначально max равнялся количеству потомков корня).
Теперь спускаемся на следующий уровень(curr теперь первый потомк предыдущего curr) засовываем в очередь всех его потомков, для них в последствии тоже будем искать максимальный. Таким образом, в этом цикле while мы постепенно поместим в очередь все узлы и посчитаем для них максимальную степень, последовательно удаляя из очереди.
Когда очередь опустеет, цикл while закончится и функция вернет max.
#define new_tree malloc(sizeof(tree_item));
typedef struct Tree_item tree_item;
struct Tree_item {
struct Tree_item* child;
struct Tree_item* brother;
int value;
};
int max(int a, int b) {
return a > b ? a : b;
}
int tree_power(tree_item* tree) {
if (tree == 0) {
return 0;
}
if (tree->child == 0) {
return 0;
}
int cur_pow = 0;
tree_item* temp = tree->child;
while (temp != 0) {
temp = temp->brother;
cur_pow++;
}
temp = tree->child;
for (int i = 0; i < cur_pow; ++i) {
int child_pow = tree_power(temp);
if (child_pow > cur_pow) {
cur_pow = child_pow;
}
temp = temp->brother;
}
return cur_pow;
}
2 билет (Сравнение двух линейных списков)
Пусть элемент списка имеет структурный тип item с полями int data-значение и item* next-указатель на следующий элемент; список имеет структурный тип list
с полями int size-количество элементов и item* head-указатель на голову списка.
Список - структура с последовательным доступом к элементу, поэтому сравнить два списка мы можем только с помощью последовательного сравнения пар элементов.
1. Передаем два списка в функцию сравнения по ссылке, используя & (взятие адреса)
2. Сравниваем поле size этих списков; если значение не совпадает функция возвращает false.
3. Инициализируем две переменные типа item*: curr1 и curr2 - указатели на элементы списка. Одной из них присваиваем значение указатели на голову первого списка,
второй - значение указателя на голову второго. Проходим по элементам списков с помощью цикла for, используя итератор i, (i = 0; i < size; i++).
В каждой итерации сравниваем поля data элементов, на которые в данный момент указывают curr1 и curr2. Если они не равны, функция возвращает false. Присваиваем указателям curr1 и curr2
значения указателей на следующий элемент.
4. Цикл завершен, все элементы совпадают - возвращаем true.
Сложность - O(N)- линейный проход по спискам.
main.c
#include
#include "list.h"
int main(void) {
int n, m, i, v;
list xs1, xs2;
printf("Введите кол-во элементов в первом списке: ");
scanf("%d", &n);
printf("Введите кол-во элементов во втором списке: ");
scanf("%d", &m);
list_create(&xs1);
list_create(&xs2);
printf("Заполняем первый список:\n");
for (i = 0; i < n; ++i) {
printf("> ");
scanf("%d", &v);
list_push(&xs1, v);
}
printf("Заполняем второй список:\n");
for (i = 0; i < m; ++i) {
printf("> ");
scanf("%d", &v);
list_push(&xs2, v);
}
if (list_compare(&xs1, &xs2)) {
printf("Списки равны.\n");
} else {
printf("Списки не равны.\n");
}
list_destroy(&xs1);
list_destroy(&xs2);
return 0;
}
list.h
#ifndef LIST_H
#define LIST_H
#include
#include
typedef struct _list_item {
struct _list_item * next;
int data;
} list_item;
typedef struct _list {
int size;
struct _list_item * head;
} list;
void list_create(list * xs);
void list_push(list * xs, int value);
bool list_compare(list * xs1, list * xs2);
void list_destroy(list * xs);
#endif
list.c
#include "list.h"
void list_create(list * xs) {
xs->head = malloc(sizeof(list_item));
xs->head->next = NULL;
xs->size = 0;
}
void list_push(list * xs, int value) {
if (xs->size == 0) {
xs->head->data = value;
} else {
list_item * curr;
w list_item * tmp = malloc(sizeof(list_item));
tmp->data = value;
curr = xs->head;
while (curr->next != NULL) {
curr = curr->next;
}
curr->next = tmp;
}
xs->size++;
}
bool list_compare(list * xs1, list * xs2) {
if (xs1->size != xs2->size) {
return false;
} else {
int i;
list_item * curr1, * curr2;
curr1 = xs1->head;
curr2 = xs2->head;
for (i = 0; i < xs1->size; i++) {
if (curr1->data != curr2->data) {
return false;
}
curr1 = curr1->next;
curr2 = curr2->next;
}
return true;
}
}
void list_destroy(list * xs) {
list_item * curr,
* prev,
* tmp;
curr = xs->head;
if (curr->next == NULL) {
free(curr);
curr = NULL;
return;
}
while (curr != NULL) {
prev = curr;
tmp = curr->next;
free(prev);
curr = tmp;
}
}
3 билет (Реверс дека)
Пусть проинициализирован дек d, заданы функции push_back - добавить элемент в конец и push_front - добавить элемент в начало.Произведем реверс дека с помощью переноса всех элементов в вспомогательный дек,
а затем перенесем элементы обратно в основной дек, но уже в обратном порядке.
1.Проинициализируем вспомогательный дек tmp.
2. В цикле while, пока размер дека d больше нуля будем извлекать очередной элемент из конца основного дека d и помещать его в конец вспомогательного дека tmp.В итоге в tmp будет обратный
порядок следования элементов.
3.Перенесем элементы обратно в основной дек, не меняя их порядка.В цикле while пока размер дека tmp больше нуля будем извлекать очередной элемент из конца дека tmp и помещать его
в начало дека d. В итоге d окажется реверснутым.
Сложность O(N)
#include
#include "dequeue.h"
int main(void) {
int val, n, i;
dequeue d, tmp;
dequeue_create(&d);
dequeue_create(&tmp);
printf("Введите кол-во чисел: ");
scanf("%d", &n);
printf("Вводите числа:\n");
for (i = 0; i < n; i++) {
scanf("%d", &val);
dequeue_push_back(&d, val);
}
printf("Исходный дек:\n");
dequeue_print(&d);
while (d.size > 0) {
val = dequeue_pop_back(&d);
dequeue_push_back(&tmp, val);
}
while (tmp.size > 0) {
val = dequeue_pop_front(&tmp);
dequeue_push_back(&d, val);
}
printf("Перевёрнутый дек:\n");
dequeue_print(&d);
dequeue_destroy(&d);
dequeue_destroy(&tmp);
return 0;
}.
4 билет (Глубина дерева)
Ну там просто спускаешься вниз максимально
По сыновьям
Потом смотришь братьев от младших сыновей к старшим и опять пытаешься спуститься
Максимально
Сложность – O(N), если максимальная глубина
Если не максимальная, то сложность O(N*logN)
typedef struct node { int key;
struct node *son; struct node *brother;
} tree; //описание структуры дерева
void deepth(tree *root, int *h, int count) { if (root != NULL) {
if (count > *h)
*h = count;
deepth(root->son, h, count + 1); deepth(root->brother, h, count);
}
} //функция определения глубины дерева
В функцию передается указатель на переменную изначально равную h = 0 и переменная count = 0. Выводим значение переменной h, которая равна глубине дерева.
int main() {
…
int h = 0; deepth(kor, &h, 0);
printf("deepth_tree=%d\n", h);
…
}
И другие функции работы с деревом общего вида.
5 билет (Нахождение одинаковых элементов бинарного дерева)
1) Берём пустой список)
Двигаемся по дереву по-любому из алгоритмов обхода дерева - (например dfs, bfs - поиски в глубину и ширину) - записывая вершины в список
Сортируем полученный список какой-нибудь сортировкой (я начала описывать сортировку слиянием, чел сказал "да какая разница, что за сортировка", я сказала "ну как же, хочу время сократить", он сказал " ну Ок допустим")
Заведем переменную tmp = 0
Теперь будем двигаться по этому списку:
Так как нам нужно посчитать количество различных элементов, то если следующий элемент != данному, то tmp++.
Код левый, не по алгоритму
typedef struct node { int key;
struct node *left; struct node *right;
}tree;
void same(tree *root, int k) { if (root == NULL)
return;
if (root->key == k) { printf("Repeat found: "); printf("%d\n", root->key);
}
same(root->left, k); same(root->right, k);
}
6 билет (Реверс файла)
Алгоритм:
Воспользуемся стеком.
Файл можно читать только последовательно, с начала. Будем последовательно считывать символы из файла.В переменной char c будем хранить текущий прочитанный символ.
Функция reverse_file:
1.Сохраняем прочитанный символ из файла input в переменной c с помощью fgetc()
2. Снова рекурсивно запускаем функцию reverse_file
3. Помещаем значение переменной c в результирующий файл output с помощью fputc()
Таким образом, благодаря рекурсии, символы файла помещаются в стек памяти. Затем, когда прочитан последний символ, мы
переносим элементы этого стека в файл output, начиная с последнего элемента файла(так как он поступил в стек последним-выйдет первым). Та
ким образом, символы файла input будут помещены в файл output в обратном порядке.
void reverse_file(FILE * input, FILE * output){
char c;
if(feof(input)) {
return;
} else {
c = fgetc(input);
reverse_file(input, output);
fputc(c, output);
}
}
int main(int argc, char * argv[]) {
FILE * input, * output;
input = fopen(argv[1], "r");
output = fopen(argv[2], "w");
reverse_file(input, output);
return 0;
}
7 билет (Сортировка стека *слиянием*)
Сперва сам алгоритм: идея в том, чтобы завести второй стек, элементы в котором будут отсортированы между итерациями. В конце работы он будет содержать все элементы исходного в отсортированном порядке.
Снимаем с верхушки исходного стека элемент x.
Находим позицию, в которую его можно добавить во временный стек, такую, чтобы не нарушался инвариант. Эта позиция - либо единственно возможная, если временный стек пуст, либо сразу после элемента, который больше x, ибо тогда ниже в стеке окажутся элементы меньшие или равные (напоминаю, временный стек всегда отсортирован). Для того, чтобы x поместить в эту позицию, мы последовательно вынимаем из стека все, что нам мешает, и кладем в исходный стек (позже мы все равно это отсортируем). (строчки 2 и 3)
Помещаем x во временный стек. Временный стек остается отсортирован после этого шага. (строчка 4)
Повторяем до тех пор, пока в исходном стеке не осталось элементов. (строчка 1)
При особенно сильном желании вернуть именно исходный стек всегда в конце можно вынуть все элементы из временного и поместить в исходный, предварительно переделав сравнение.

void reverse(stack *a) { stack *b; create(&b);
while (!isEmpty(a))
push(b, pop(a)); copy(b, a);
} //функция реверса стека
stack *merge(stack *a, stack *b) { stack *res;
create(&res);
while (!isEmpty(a) && !isEmpty(b)) { if (top(a) < top(b))
push(res, pop(a));
else
push(res, pop(b));
while (!isEmpty(a))
push(res, pop(a)); while (!isEmpty(b))
push(res, pop(b));
}
reverse(res); return res;
} //функция слияния двух стеков
void merge_sort(stack **x) { if (size(*x) > 1) {
int l = size(*x) / 2 stack *a, *b;
create(&a); create(&b);
for (int i = 0; i < l; i++) push(a, pop(*x));
while (!isEmpty(*x)) push(b, pop(*x));
merge_sort(&a); merge_sort(&b);
*x = merge(a, b);
}
} //функция сортировки стека слиянием
8 билет Транспонирование матрицы из файла
Алгоритм через файлы:
сначала мы считаем количество строк и слов в каждой строке
после этого
пишем функцию, копирующую одно слово в новый файл
что-то типа, берем getchar() пока не дойдем до пробела " "
далее само транспонирование сделаем так
выпишем исходную матрицу в новый файл в одну строку
это можно сделать оператором fgets
он читает по строкам
применяем его просто столько раз сколько у нас строк (это мы посчитали заранее)
итого у нас есть исходная матрица, записанная в строку
в новом файле
далее, стираем старый файл, открываем его для записи
и далее, вложенным циклом, где внешний цикл - поколичеству столбцов, а внутренний - по количеству строк
копируем каждый N-ый символ в пустой файл
где N это количество столбцов
потом ставим знак "\n"
таким образом, мы скопируем все элементы в нужном порядке по строкам

Решение через массив ( многие лабники ФИИТ опрокинули ):
#include
#include
#include
#define MAX_DIMENTION 1000
int main(void) {
int num, // текущее число
offset, // отступ для sscanf
// счётчики размерности матрицы
i,
j,
//
n,
m,
matrix[MAX_DIMENTION][MAX_DIMENTION]; // массив для матрицы
char * line; // текущая строка
size_t len = 0; // длина считанной строки
FILE * input_file = NULL;
input_file = fopen("input.txt", "r");
// заполняем массив
i = 0;
while (getline(&line, &len, input_file) != -1) {
j = 0;
while (sscanf(line, " %d%n", &num, &offset) == 1) {
matrix[i][j++] = num;
line += offset;
}
i++;
}
// выводим результат
for (n = 0; n < j; n++) {
for (m = 0; m < i; m++) {
printf("%d ", matrix[m][n]);
}
printf("\n");
}
return 0;
}
9 билет (Подсчет количества различных элементов бинарного дерева)
Задаем структуру для вектора ( определяем указатель на начало и конец)
задаем структуру элементу вектора (указатели на следующий, предыдущий и узел дерева), задаем структуру для узла дерева (id - хранимые данные, vector *children - вектор ссылок на всех детей данного узла).
Создадим рекурсивную функцию, которая в качестве аргументов принимает ссылку на дерево, а также ссылку на вектор для хранения результатов. Считаем сначала всех уникальных детей от переданной вершины. После выполненной операции переходим к первому children из вектора, после чего рекурсивно вызываем функцию, куда в качестве аргументов передаём curr, а также вектор для хранения результатов. Цикл мы вызываем рекурсивно в цикле while, условие завершение которого - while (curr != null). при этом curr с каждой итераций становится равным своему “брату” (curr -> next). в конце выполнения возвращаем вектор с уникальными эл-ми.
Сложность - О(N*M) - где M - потенциальное кол-во уникальных эл-ов.
Решение:
Делаем обход в ширину и заносим уникальные вершины в новый вектор
typedef struct _vector_item {
struct _vector_item * next;
struct _vector_item * prev;
struct _tree_node * node;
} vector_item;Нет
typedef struct _vector {
int size;
struct _vector_item * front;
struct _vector_item * back;
} vector;
typedef struct _tree_node {
char id;
vector * children;
} tree_node;
vector * find_same_nodes(tree_node * tree, vector *result) {
vector_item * curr;
vector queue;
vector_create(&queue);
curr = tree->children->front;
while (curr != NULL) {
vector_push_back(&queue, curr);
curr = curr->next;
}
while (queue.size > 0) {
curr = vector_pop_front(&queue);
if (result.size == 0 || vector_in(&result, curr) == 0) {
vector_push_back(&result, curr);
}
}
curr = curr->node->children->front;
while (curr != NULL) {
(*result) = find_same_nodes(&(curr->node), &(*result))
curr = curr->next;
}
vector_destroy(&queue);
return &result;
}
10 Удаление листов
Рассмотрим удаление листов для обычного дерева. Структура у нас описана следующим образом - в структуре листа дерева есть ссылки на сына и брата, также хранится значение, которое принадлежит данному листу. Программа на вход должна принимать значение, которое необходимо удалить. После чего мы ищем“брата” листа, в котором находиться значение, которое нам нужно удалить. Если брат есть, то мы смещаем его на позицию удаляемого листа, а на позицию брата ставим брата брата, и т.д., пока не дойдём до нулевой ссылки на брата. Если же брата нет, то мы ищем “отца” листа, и делаем там ссылку на son равной 0 (не забывая при этом son->data сделать равной 0)
typedef node * link;
struct node
{ tdata data;
link son;
link brother;
};
link searchfather(link tree, tdata c) //поиск отца элемента c
{ link t; if(tree) // если дерево не пустое
{ if(tree->son&&tree->son->data==c) return tree; //если сын равен c то возращаем текущий элемент
t=tree->son; //запоминаем сына
while(t) { if(t->brother&&t->brother->data==c) return tree;
t=t->brother; //проверяем его братьев, если есть с, возвращаем текущий элемент
}
t=0; t=searchfather(tree->son,c); //ищем элемент с в ветке сына
if(!t) t=searchfather(tree->brother,c); // если элемента c нет у одного сына, то ищем у его брата
return t;
} return 0;
}
link searchbrother(link tree, tdata c) //ищем брата с
{ if(tree) //если дерево не пустое
{ if(tree->brother&&tree->brother->data==c) return tree; // если брат равен с, возврпащаем текущий элемент
link t=searchbrother(tree->brother,c); // ищем у брата
if(!t) t=searchbrother(tree->son,c); // если не нашли начинаем проверять братьев у сына
return t;
} return 0;
}
printf("\nInput value of node ==>"); scanf(" %c",&f); // вводим значение элемента на удаление
if(tree->data==f)if(tree->brother==0) tree=0; //если равен значению и нет братьев то обнуляем
else tree=tree->brother; // если брат есть переходим к нему
else { t=searchbrother(tree,f); // иначе ищем брата нашего значения
if(t) t->brother=t->brother->brother; //освобождаем значение от братьев
else { t=searchfather(tree,f); //если у значения нет братьев ищем отца
if(t) if(t->son->brother) t->son=t->son->brother; //если брат все же есть убираем
else t->son=0; // иначе обнуляем наше значение
else printf("\nNode not found\n"); // если такого значения вообще нет
}
}
11 билет Конкатенация трех файлов
int main()
{
unsigned char ch; // Так как бинарный режим чтения файлов, то нужен диапозон значений 0 - 255
FILE *f1 = fopen("f1.bin", "rb");
FILE *f2 = fopen("f2.bin", "rb");
FILE *f3 = fopen("f3.bin", "rb");
FILE *f = fopen("f.bin", "wb");
while (fread(&ch, 1, 1, f1)
fwrite(&ch, 1, 1, f);
while (fread(&ch, 1, 1, f2))
fwrite(&ch, 1, 1, f);
while (fread(&ch, 1, 1, f3))
fwrite(&ch, 1, 1, f); fclose(f1);
fclose(f2); fclose(f3); fclose(f); return 0;
} // вариант с бинарным файлом
int main() {
FILE *f1 = fopen("f1.txt", "r");
FILE *f2 = fopen("f2.txt", "r");
FILE *f3 = fopen("f3.txt", "r");
FILE *f = fopen("f.txt", "w"); char c = '\0';
while ((c = getc(f1)) != EOF) putc(c, f);
while ((c = getc(f2)) != EOF) putc(c, f);
while ((c = getc(f3)) != EOF) putc(c, f);
fclose(f1); fclose(f2); fclose(f3); fclose(f); return 0;
} //вариант с текстовым файлом
12 билет Задача - не рекурсивная сортировка Хоара
Заведем структурный тип t, в котором будем хранить текущие границы.
Элементы типа t будем хранить в стеке.создадим стек и занесем туда первый элемент со значениями L = 1 и R = n;
Функция сортировки, пока стек не пуст:
Достанем из стека первый элемент-текущие границы L и R. Произведем первую сортировку - сортировку всей последовательности, зерновой элемент в середине.
После того, как произвели сортировку всей последовательности, откладываем запрос на сортировку правой половины(т.е. границы правой половины) в стек. После этого присваиваем R значение j - итератора, который двигался влево. Таким образом, L и R теперь ограничивают левую часть массива и в следующей итерации цикла сортировка этой части будет выполнена немедленно. Потом и правая отсортируется когда-нибудь.
Число сравнений в быстрой сортировке равно nlogn, число перестановок - nlogn/6. Недостаток - низкая производительность при небольших n.
Рекурсивная и нерекурсивная версии имеет одинаковую временную сложность
void Quick(int arr[], int n)
{
int base, left, right, i, j; base = left = right = i = j = 0; stack *st;
push(st, n - 1);
push(st, 0); do {
left = Pop(&st); right = Pop(&st);
if (((right - left) == 1) && (arr[left] > arr[right]))
swap(arr[left], arr[right]); else {
base = arr[(left + right) / 2]; i = left;
j = right; do {
while ((base > arr[i]))
++i;
while (arr[j] > base)
--j;
if (i <= j)
swap(arr[i++], arr[j--]);
} while (i <= j);
}
if (left < j) {
push(st, j); push(st, left);
}
if (i < right) {
push(st, right); push(st, i);
}
} while (top(st) != NULL);
}
13 Вычислить константное булевое выражение с помощью обратной польской записи
Примечание: выражение вводится в постфиксной форме.
#include
#include "stack.h"
int main() {
char c, a, b;
stack s;
stack_create(&s);
while ((c = getchar()) != EOF) {
if (c == '0' || c == '1') {
stack_push(&s, c - '0');
} else if (c == '+') {
a = stack_pop(&s);
b = stack_pop(&s);
if (a && b)
stack_push(&s, a);
else
stack_push(&s, a + b);
} else if (c == '*') {
a = stack_pop(&s);
b = stack_pop(&s);
stack_push(&s, a * b);
}
}
printf("%d\n", stack_top(&s));
return 0;
}
14 билет (Проверить вложенность скобок *через стек*)
int main() {
int i = 0; char a[100], x;
stack *a = NULL; scanf("%s", a);
while (a[i] != '\0') {
if a[i] == '(' {
x = a[i];
push(a, x);
}
if a[i] == ')'{
if a[i] == top()
pop(&a); else {
printf("False\n"); return 1;
}
} i++;
}
if (top() != NULL)
printf("False\n")
else
printf("True\n");
return 0;
}
15 Составить прогу вычисляющую арифметическое выражение из чисел с обратной польской записью
Удобство обратной польской нотации заключается в том, что выражения, представленные в такой форме, очень легко вычислять, причём за линейное время. Заведём стек, изначально он пуст. Будем двигаться слева направо по выражению в обратной польской нотации; если текущий элемент — число или переменная, то кладём на вершину стека её значение; если же текущий элемент — операция, то достаём из стека два верхних элемента (или один, если операция унарная), применяем к ним операцию, и результат кладём обратно в стек. В конце концов в стеке останется ровно один элемент - значение выражения.
Очевидно, этот простой алгоритм выполняется за 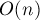 , т.е. порядка длины выражения. , т.е. порядка длины выражения.
#include
#include
#include
const int N = 20;
typedef struct _stack_item
{
struct _stack_item * next;
struct _stack_item * prev;
char data;
} stack_item;
typedef struct _stack
{
int size;
struct _stack_item * head;
} stack;
void stack_create(stack * s)
{
s->head = NULL;
s->size = 0;
}
void stack_push(stack * s, char value)
{
stack_item * tmp;
tmp = malloc(sizeof(stack_item));
tmp->data = value % 48;//******ВАЖНО******
if (s->size == 0)
tmp->prev = NULL;
s->head = tmp;
else
tmp->prev = s->head;
s->head->next = tmp;
s->head = tmp;
s->size++;
}
char stack_pop(stack * s)
{
char val;
stack_item * tmp;
val = s->head->data;
tmp = s->head->prev;
free(s->head);
s->head = tmp;
s->size--;
return val;
}
void stack_destroy(stack * s)
{
while (s->size > 1)
stack_pop(s);
free(s->head);
s->head = NULL;
s->size = 0;
}
int isNotEmpty(stack * s)
{
if (s->size == 0)
return 0;
else
return 1;
}
int main()
{
setlocale(LC_ALL, "rus");
char s[N];
scanf("%s",s);
int i = 0;
printf("Введенное выражение: ");
while (s[i] != '\0')
printf("%c",s[i]);
i += 1;
printf("\n");
i = 0;
stack st;
stack_create(&st);
while (s[i]!='\0')
if (s[i]>='0' && s[i]<='9')
stack_push(&st, s[i]);
if (s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/')
char tmp1;
char tmp2;
tmp2 = stack_pop(&st);//читаем ведь с лева на право
tmp1 = stack_pop(&st);
if (s[i] == '+')
stack_push(&st, tmp1 + tmp2);
else if (s[i] == '-')
stack_push(&st, tmp1 - tmp2);
else if (s[i] == '*')
stack_push(&st, tmp1 * tmp2);
else if (s[i] == '/')
stack_push(&st,tmp1 / tmp2);
i += 1;
char result = stack_pop(&st);
printf("Значение выражения: %d", result);
return 0;
}
else
printf("True\n");
return 0;
}
16 билет (Удаление из дерева выражения *1 и +0)
В дереве могут быть операции *1 или 1* (порядок не важен)
Ищем вершину, в которой операция *
Смотрим, есть ли в детях число 1
Если есть, удаляем
Смотрим корень и операцию, которую он хранит
Если это нужные нам "*" или "+", смотрим какие операнды (числа) она складывает: проверяем детей. Если хотя бы в одном из детей есть 1 (для *) или 0 (для +), удаляем обоих детей (дерево же бинарное) и сам корень
Тот же алгоритм применяем для детей и их детей, и их детей...
Это просто дерево выражения
А там могут быть всякие любые операции от деления до степени
Суть данной задачи в том, что эти выражения не имеют смысла
a * 1 = a
Поэтому мы хотим их удалить
if ((root->key == '*') && ((root->left->key == '1') || (root->right->key == '1'))) {
if (root->left->key == '1') { free(root->left);
tmp = root->right; free(root);
root = tmp;
}
}
if ((root->key == '*') && ((root->left->key == '1') || (root->right->key == '1'))) {
if (root->right->key == '1') { free(root->right);
tmp = root->left; free(root);
root = tmp;
}
}
if ((root->left->key == '*') && ((root->left->left->key == '1') || (root-
>left->right->key == '1'))) {
if (root->left->left->key == '1' ) { free(root->left->left);
root->left = root->left->right;
}
}
if ((root->left->key == '*') && ((root->left->left->key == '1') || (root-
>left->right->key == '1'))) {
if (root->left->right->key == '1') { free(root->left->right);
root->left = root->left->left;
}
}
if ((root->right->key == '*') && ((root->right->left->key == '1') || (root-
>right->right->key == '1'))) {
if (root->right->left->key == '1') { free(root->right->left);
root->right = root->right->right;
}
}
if ((root->right->key == '*') && ((root->right->left->key == '1') || (root-
>right->right->key == '1'))) {
if (root->right->right->key == '1') {
free(root->right->right);
root->right = root->right->left;
}
}
if (root->left != NULL && root->left->left != NULL && root->left->right != NULL)
task(root->left);
if (root->right != NULL && root->right->left != NULL && root->right->right != NULL)
task(root->right);
}
Реализация +0 аналогичным способом
void transtree(link &tree)
{ char c, cl, cr, cl1, cr1;
if(tree)
{if(tree->data=='*')
{ cl=tree->left->data; cr=tree->right->data;
if (cl == '1' && cr == '1'){
tree->data = '1';
tree->right = NULL;
tree->left = NULL;
delete(tree->right);
delete(tree->left);
}
if (cl == '1' && cr != '1'){
link t = tree->right;
tree->right = NULL;
tree->left = NULL;
delete(tree->right);
delete(tree->left);
tree = t;
printf("data - %c \n",tree->data);
}
if (cr == '1' && cl != '1'){
link t = tree->left;
tree->right = NULL;
tree->left = NULL;
delete(tree->right);
delete(tree->left);
tree = t;
printf("data - %c \n",tree->data);
}
}
transtree(tree->left);
transtree(tree->right);
}
} |
|
|
 Скачать 176.26 Kb.
Скачать 176.26 Kb.

