информатикаа. Ункция это множество точек (x, y), удовлетворяющее выражению yf(x). 1) График линейной функции y5x2
 Скачать 167.35 Kb.
|
|
ункция -это множество точек (x, y), удовлетворяющее выражению y=f(x). 1) График линейной функции: y=5x-2 Г 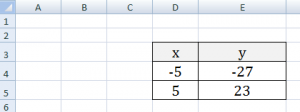 рафиком линейной функции является прямая, которую можно построить по двум произвольным точкам. Создадим таблицу, выполним вычисления.Для построения графика необходимо выделить полученную таблицу и выбирать опцию меню: Вставка - Точечная – Точечная с гладкими кривыми и маркерами. 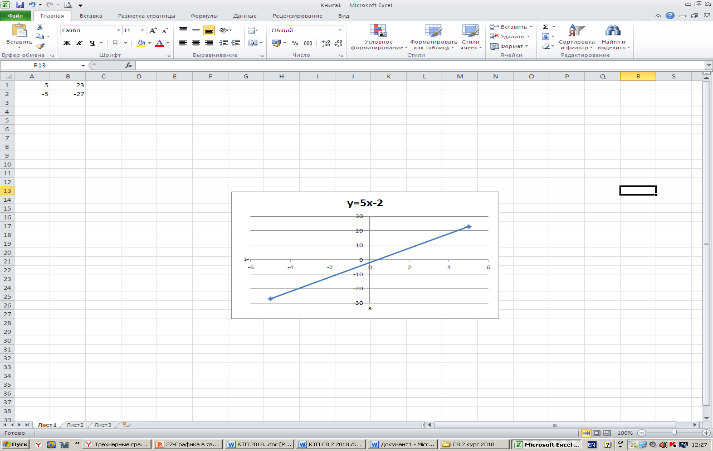 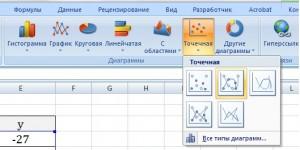  Замечание. Для изменения параметров осей используйте опцию меню Конструктор – Выбрать данные 2) График квадратичной функции – параболы y=2x2-2 П 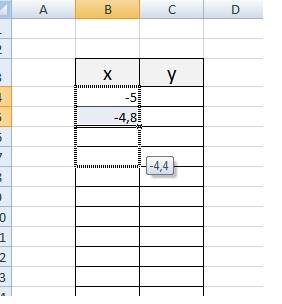 араболу по двум точкам уже не построить, в отличии от прямой.Создадим таблицу, выполним вычисления: Зададим интервал на оси x, на котором будет строиться парабола, например [-5; 5]. Зададим шаг (чем меньше шаг, тем точнее будет построенный график), например, 0,2. Рассчитаем столбец значений у. Действуем аналогично построению графика линейной функции. П 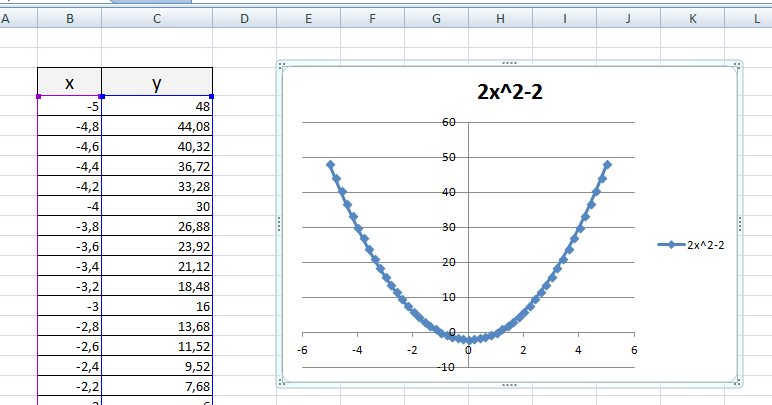 олучим:Замечание. Чтобы не было точек на графике, поменяйте тип диаграммы на Точечная с гладкими кривыми. 3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм. Р 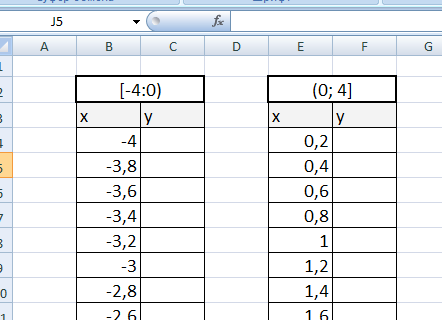 ассмотрим это на примере функции у=1/х.Функция определена на интервалах (- беск;0) и (0; +беск) Создадим график функции на интервалах: [-4;0) и (0; 4]. Подготовим две таблицы, где х изменяется с шагом 0,2: Находим значения функции от каждого аргумента х аналогично примерам выше. На диаграмму необходимо добавить два ряда - для первой и второй таблички соответственно. Далее нажимаем кнопку Добавить и заполняем таблицу Изменение ряда значениями из второй таблицы. |