лллл. Практическое № 11 Уравнения плоскости и прямой в пространстве. Уравнения плоскости и прямой в пространстве
 Скачать 16.89 Kb. Скачать 16.89 Kb.
|
|
Уравнения плоскости и прямой в пространстве 1. Найдите координаты: а) точки 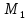 – проекции точки – проекции точки  на плоскость на плоскость 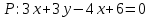 ; б) точки ; б) точки  , симметричной точке , симметричной точке 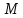 относительно плоскости относительно плоскости  . .2. Найдите уравнение плоскости, проходящей через прямую  , заданную в виде пересечения двух плоскостей: , заданную в виде пересечения двух плоскостей: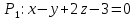 и и  , ,Перпендикулярно другой плоскости 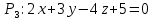 . .3. Исследуйте взаимное расположение прямой  и плоскости: а) и плоскости: а)  ; б) ; б) 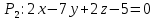 ; в) ; в) 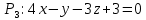 . Если прямая и плоскость параллельны, то найдите расстояние между ними, а если пересекается, то найдите координаты точки пересечения и угол между ними. . Если прямая и плоскость параллельны, то найдите расстояние между ними, а если пересекается, то найдите координаты точки пересечения и угол между ними.4. Докажите, что прямые 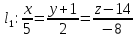 и и  параллельны и а) найдите расстояние между ними; б) составьте уравнение плоскости параллельны и а) найдите расстояние между ними; б) составьте уравнение плоскости  , проходящей через эти прямые. , проходящей через эти прямые.5. Докажите, что прямые  и и 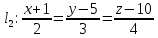 пересекаются и а) найдите координаты точки пересечения; б) составьте уравнение плоскости, содержащей эти прямые. 6. Даны координаты точек:  , ,  и и  . Найдите: а) периметр треугольника . Найдите: а) периметр треугольника  ; б) угол ; б) угол  ; в) площадь треугольника ; в) площадь треугольника  ; г) уравнение прямой треугольника ; г) уравнение прямой треугольника 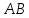 ; д) уравнение плоскости треугольника ; д) уравнение плоскости треугольника  . .7. Даны координаты четырёх точек:  , , 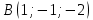 , , 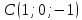 и и  : :a) докажите, что эти точки не лежат в одной плоскости; b) найдите уравнение плоскости  ; ;c) найдите уравнение прямой  ; ;d) найдите площадь треугольника  ; ;e) найдите уравнение и длину высоты пирамиды  , опущенной из вершины , опущенной из вершины  на основание на основание  ; ;f) определите координаты точки  – основания высоты (из п. е) – основания высоты (из п. е)g) найдите угол между ребром  и основанием и основанием  h) найдите угол между гранями  и и  ; ;i) вычислите объём пирамиды. |
