Бинарные деревья. Урок 8. Конспект. Урок Бинарные деревья
 Скачать 1.62 Mb.
|
  Урок 8. Бинарные деревья |
| class BinaryTree: def __init__(self, root_obj): # корень self.root = root_obj # левый потомок self.left_child = None # правый потомок self.right_child = None # добавить левого потомка def insert_left(self, new_node): # если у узла нет левого потомка if self.left_child is None: # тогда узел просто вставляется в дерево # формируется новое поддерево self.left_child = BinaryTree(new_node) # если у узла есть левый потомок else: # тогда вставляем новый узел tree_obj = BinaryTree(new_node) # и спускаем имеющегося потомка на один уровень ниже tree_obj.left_child = self.left_child self.left_child = tree_obj # добавить правого потомка def insert_right(self, new_node): # если у узла нет правого потомка if self.right_child is None: # тогда узел просто вставляется в дерево # формируется новое поддерево self.right_child = BinaryTree(new_node) # если у узла есть правый потомок else: # тогда вставляем новый узел tree_obj = BinaryTree(new_node) # и спускаем имеющегося потомка на один уровень ниже tree_obj.right_child = self.right_child self.right_child = tree_obj # метод доступа к правому потомку def get_right_child(self): return self.right_child # метод доступа к левому потомку def get_left_child(self): return self.left_child # метод доступа к корню def get_root_val(self): return self.root r = BinaryTree(8) print(r.get_root_val()) print(r.get_left_child()) r.insert_left(25) print(r.get_left_child()) print(r.get_left_child().get_root_val()) r.insert_right(6) print(r.get_right_child()) print(r.get_right_child().get_root_val()) print(r.get_right_child().get_root_val()) |
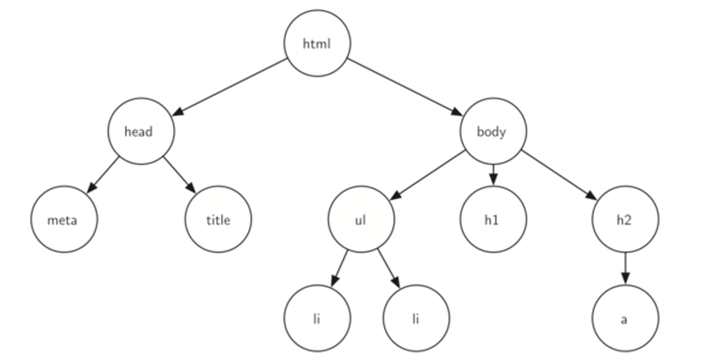
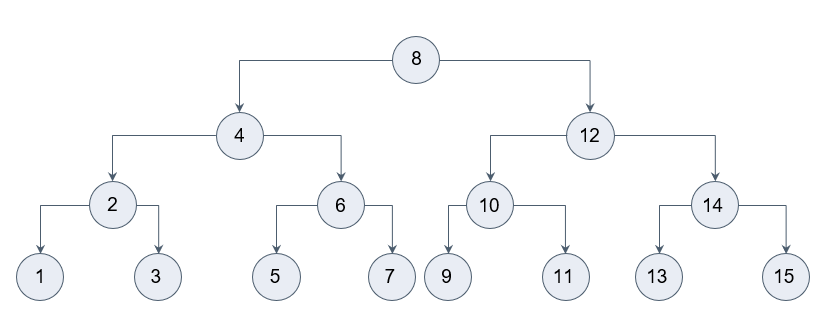
В приведенном примере мы создали простое дерево с узлом 8 в качестве корня и узлами 4 и 12 в качестве левого и правого потомков, соответственно. Обратите внимание, что левый и правый потомки корня являются сущностями класса BinaryTree. Таким образом, мы видим рекурсивное определение дерева. Это позволяет нам работать с любым потомком двоичного дерева, как с самим деревом.ЗАЧЕМ НУЖНЫ БИНАРНЫЕ ДЕРЕВЬЯ И ГДЕ ПРИМЕНЯЮТСЯ
Основное назначение двоичных деревьев заключается в повышении эффективности поиска. При поиске выполняются такие операции, как нахождение заданного элемента из набора различных элементов, определение наибольшего или наименьшего элемента в наборе, фиксация факта, что набор содержит заданный элемент. На практике двоичные деревья поиска очень удобны во многих приложениях, где входные данные случайны или есть другие причины надеяться на сохранение деревом хорошей формы.
Что же касается в целом деревьев, то в различных задачах применяются различные виды деревьев, например,
при разработке парсеров или трансляторов полезным может оказаться дерево синтаксического разбора (синтаксическое дерево);
при работе со строками удобными могут оказаться суффиксные деревья;
при разработке оптимальных алгоритмов на графах полезным может оказаться структура данных в виде кучи;
двоичные деревья поиска используются при реализациях словаря, они являются достаточно простым и распространенным видом деревьев, поэтому их мы рассмотрим более подробно;
В большинстве реляционных СУБД в качестве структуры данных для индексов (та или иная их реализация) используются именно деревья.
Сами по себе деревья бесполезны, если мы не выполняем с ними определенные операции. К таким операциям обычно относят: поиск элемента, поиск минимального (максимального) элемента, вставка, удаление.
ЭФФЕКТИВНОСТЬ
ПРИМЕНЕНИЕ БИНАРНОГО ДЕРЕВА ДЛЯ РЕАЛИЗАЦИИ АЛГОРИТМА КОДИРОВАНИЯ ПО ХАФФМАНУ
В основе идеи кодировании Хаффмана – подсчет частоты появления символа в последовательности. Символ, который встречается чаще всего, получает новый, очень маленький код. Наиболее редки символ, напротив, получает очень длинный код.
В следующем примере символ будет иметь длину 8 бит.
Рассмотрим применение алгоритма Хаффмана. Допустим, у нас есть строка «beep boop beer!», для которой на каждый знак тратится по одному байту. Это означает, что вся строка занимает 15*8 = 120 бит памяти. После кодирования – 40 бит.
Чтобы получить код для каждого символа, нужно построить бинарное дерево, где каждый лист будет содержать символ. Символы с меньшей частотой будут дальше от корня, чем символы с большей.
Посчитаем частоты всех символов.
После вычисления частот создадим узлы бинарного дерева для каждого символа и добавим их в очередь, используя частоту в качестве приоритета. В начале очереди окажутся символы с наименьшей частотой, с наибольшей – в конце.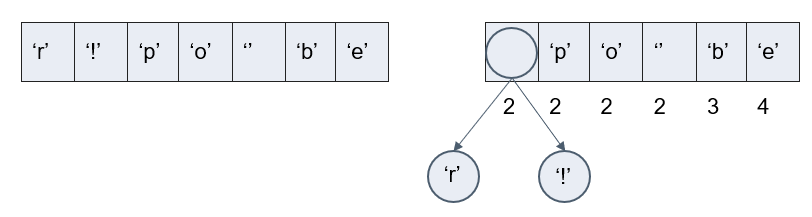
Берем из очереди два элемента с наименьшими частотами и связываем их, создавая новый узел дерева. В нем они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. Добавим получившийся узел обратно в очередь.
Повторим те же шаги необходимое количество раз.
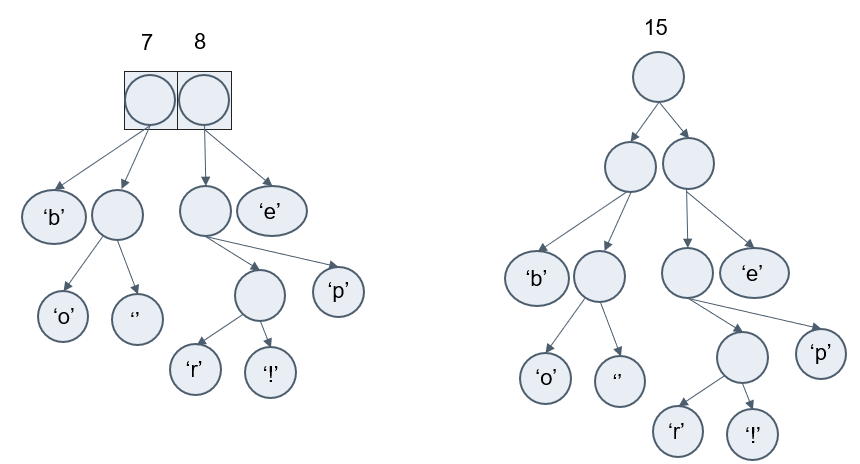
В конце свяжем два последних элемента и получится итоговое дерево.
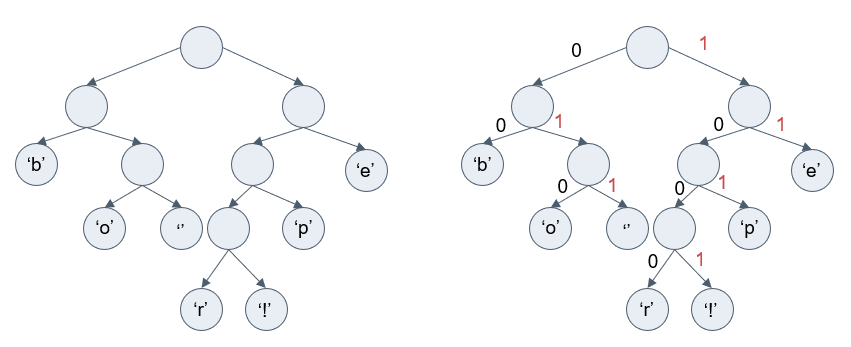
Чтобы получить код для каждого символа, надо просто пройтись по дереву и для каждого перехода добавлять 0, если мы идем влево, и 1 – если направо.
Получим следующие коды для символов:
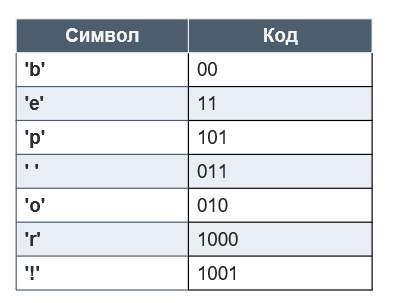
На практике при реализации данного алгоритма сразу после создания дерева строится таблица Хаффмана. Она содержит каждый символ и его код, потому что это делает кодирование более эффективным (по сути, это односвязный список). Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как видим, ASCII-версия строки и закодированная версия существенно различаются.
Рассмотрим варианты программной реализации алгоритма Хаффмана.
Листинг 2. task_2.py
| """Хаффманчерезколлекции""" from collections import Counter, deque def haffman_tree(s): # Считаемуникальныесимволы. # Counter({'e': 4, 'b': 3, 'p': 2, ' ': 2, 'o': 2, 'r': 1, '!': 1}) count = Counter(s) # Сортируем по возрастанию количества повторений. # deque([('r', 1), ('!', 1), ('p', 2), (' ', 2), ('o', 2), ('b', 3), ('e', 4)]) # deque([({0: 'r', 1: '!'}, 2), ('p', 2), (' ', 2), ('o', 2), ('b', 3), ('e', 4)]) sorted_elements = deque(sorted(count.items(), key=lambda item: item[1])) # Проверка, если строка состоит из одного повторяющего символа. if len(sorted_elements) != 1: # Цикл для построения дерева while len(sorted_elements) > 1: # далее цикл объединяет два крайних левых элемента # Вес объединенного элемента (накопленная частота) # веса - 2, 4, 4, 7, 8, 15 weight = sorted_elements[0][1] + sorted_elements[1][1] # Словарь из 2 крайних левых элементов, попутно вырезаем их # из "sorted_elements" (из очереди). # comb - объединенный элемент ''' {0: 'r', 1: '!'} {0: {0: 'r', 1: '!'}, 1: 'p'} {0: ' ', 1: 'o'} {0: 'b', 1: {0: ' ', 1: 'o'}} {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'} {0: {0: 'b', 1: {0: ' ', 1: 'o'}}, 1: {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'}} ''' comb = {0: sorted_elements.popleft()[0], 1: sorted_elements.popleft()[0]} # Ищем место для ставки объединенного элемента for i, _count in enumerate(sorted_elements): if weight > _count[1]: continue else: # Вставляем объединенный элемент # deque([({0: 'r', 1: '!'}, 2), ('p', 2), (' ', 2), ('o', 2), ('b', 3), ('e', 4)]) sorted_elements.insert(i, (comb, weight)) break else: # Добавляем объединенный корневой элемент после # завершения работы цикла sorted_elements.append((comb, weight)) ''' deque([({0: 'r', 1: '!'}, 2), ('p', 2), (' ', 2), ('o', 2), ('b', 3), ('e', 4)]) deque([(' ', 2), ('o', 2), ('b', 3), ({0: {0: 'r', 1: '!'}, 1: 'p'}, 4), ('e', 4)]) deque([('b', 3), ({0: ' ', 1: 'o'}, 4), ({0: {0: 'r', 1: '!'}, 1: 'p'}, 4), ('e', 4)]) deque([({0: {0: 'r', 1: '!'}, 1: 'p'}, 4), ('e', 4), ({0: 'b', 1: {0: ' ', 1: 'o'}}, 7)]) deque([({0: 'b', 1: {0: ' ', 1: 'o'}}, 7), ({0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'}, 8)]) deque([({0: {0: 'b', 1: {0: ' ', 1: 'o'}}, 1: {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'}}, 15)]) ''' else: # приравниваемыем значение 0 к одному повторяющемуся символу weight = sorted_elements[0][1] comb = {0: sorted_elements.popleft()[0], 1: None} sorted_elements.append((comb, weight)) # sorted_elements - deque([({0: {0: 'b', 1: {0: ' ', 1: 'o'}}, 1: {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'}}, 15)]) # {0: {0: 'b', 1: {0: ' ', 1: 'o'}}, 1: {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'}} # словарь - дерево return sorted_elements[0][0] code_table = dict() """ tree - { 0: {0: 'b', 1: {0: ' ', 1: 'o'}}, 1: {0: {0: {0: 'r', 1: '!'}, 1: 'p'}, 1: 'e'} } """ def haffman_code(tree, path=''): # Если элемент не словарь, значит мы достигли самого символа # и заносим его, а так же его код в словарь (кодовую таблицу). if not isinstance(tree, dict): code_table[tree] = path # Если элемент словарь, рекурсивно спускаемся вниз # по первому и второму значению (левая и правая ветви). else: haffman_code(tree[0], path=f'{path}0') haffman_code(tree[1], path=f'{path}1') # строка для кодирования s = "beep boop beer!" # функция заполняет кодовую таблицу (символ-его код) # {'b': '00', ' ': '010', 'o': '011', 'r': '1000', '!': '1001', 'p': '101', 'e': '11'} haffman_code(haffman_tree(s)) # code_table - {'b': '00', ' ': '010', 'o': '011', 'r': '1000', '!': '1001', 'p': '101', 'e': '11'} # выводим коды для каждого символа for i in s: print(code_table[i], end=' ') print() |
Для декодирования сообщения получателю необходимо сперва построить дерево, после чего он будет знать, как декодировать сообщение, чтобы прочесть оригинальное сообщение. Либо необходимо знать таблицу с символами и их кодами. Существует мнение, что кодирование по Хаффману не очень эффективно для большого количества редких элементов в огромном объеме текста. Однако эффективно для работы с документами, изображениями и т.д.