Решение задач на нахождение наибольшего и наименьшего значения функции. Урок По дисциплине Математика алгебра и начала анализа, геометрия
 Скачать 96.36 Kb. Скачать 96.36 Kb.
|
|
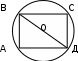
Министерство образования и молодежной политики Ставропольского края ГБПОУ Георгиевский региональный Колледж «Интеграл» Урок По дисциплине «Математика: алгебра и начала анализа, геометрия» Тема урока «Решение задач на нахождение наибольшего и наименьшего значения функции» Преподаватель Кардаильская С.А. ПЦК Естественно – научных дисциплин г. Георгиевск Тип урока: урок усвоения знаний на основе имеющихся. Цели образовательная: формировать способность применения знаний, полученных при изучении производной, для решения новых прикладных задач; развивающая: способствовать развитию математического мышления; воспитывающая: способствовать развитию логического мышления. Ход урока Организационный момент. Приветствие. Обоснование значения изучаемой темы и цели урока. План урока. Тема сегодняшнего урока – «Решение задач на нахождение наибольшего и наимень-шего значения функции». Еще в 19 в. Великий русский математик П.Л. Чебышев в своей работе «Черчение географических карт» писал, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения по возможности большей выгоды». С такими задачами приходится иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы получилось как можно больше продукции, конструкторы хотят так спланировать прибор на космическом корабле, чтобы масса прибора была наименьшей, экономисты стараются спланировать прикрепление заводов к источникам сырья так, чтобы транспортные расходы оказались минимальными. Задачи такого рода носят общее название задач на оптимизацию. В самых простых задачах, с которыми мы сегодня познакомимся, мы имеем дело с величиной, зависящей от другой величины, и надо найти такое значение второй величины, чтобы первая приняла наибольшее или наименьшее значение. С развитием информационных технологий появилась возможность упростить решение оптимизационных задач посредством составления программ, этим занимаетесь вы – программисты. Для составления программ, решающих задачи оптимизации, важно уметь построить общую математическую модель, а потом реализовать ее на языке программирования. Составлением математических моделей и их решением мы сегодня и будем заниматься. На уроках информатики вы научитесь составлять программы для решения таких задач. В курсе «Математические методы» наша задача усложнится, и мы научимся решать более сложные задачи оптимизации. Цель урока – научиться решать простейшие задачи оптимизации. План урока: 1. Проверка домашнего задания и проверка изученного. 2. Изучение нового материала. 3. Закрепление. 4. Проверка изученного (тест). Проверка домашнего задания и повторение пройденного материала. К доске вызываются двое учащихся, которые записывают решение домашних задач. В это же время остальным задаются вопросы: Назовите производную степенной функции; Назовите производную sin, cos; Что такое ускорение? Что такое скорость? Достаточный признак возрастания функции; Достаточный признак убывания функции; Признак максимума функции; Признак минимума функции. Изучение нового материала. Задача: «Число 24 представьте в виде суммы двух неотрицательных слагаемых так, чтобы сумма квадратов этих чисел была наименьшей.» Учащимся предлагается самостоятельно решить эту задачу. Они предлагают варианты ответов: 10 и 14, 5 и 19, 1 и 23, 3 и 21, 12 и 12. Правильный ответ 12 и 12. А теперь решим эту задачу, составив математическую функцию и исследовав ее на минимальное значение. 1)Пусть первое число = х, тогда второе число равно 24-х. По условию задачи сумма квадратов этх чисел должна быть наименьшей, составим функцию. f(x)= x2 + (24-x)2 2)f(x)= 2x2 – 28x + 576, Найдем производную: f,(x)= 4x – 48, Найдем нули производной: х=12, 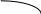  - 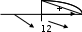 Т.к. в точке х=12 производная функции меняет знак с «- » на «+», то в этой точке функция достигает минимума. Ответ: 12 и 12. №312 Число 4 представьте в виде суммы двух неотрицательных слагаемых так, чтобы произведение этих чисел было наибольшим. Решение.1)Пусть первое число равно х, тогда второе число равно 4-х. По условию задачи произведение этих чисел должно быть наибольшим, составим функцию. f(x)= x (4 – x), 2) Найдем производную: f,(x)=4 - 2х, 3) Найдем нули производной: х= 2, 4)  -  Т. к. в точке х= 2 производная функции меняет знак с « +» на «-», то в этой точке функция достигает максимума. Ответ: 2 и 2. №319 Из круглого бревна вырезают балку с прямоугольным сечением наибольшей площади. Найдите размеры сечения балки, если радиус сечения бревна 20 см. Решение. 1)Пусть АВ= х см, тогда АД = 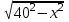 . Площадь сечения должна быть наибольшей, т.е. . Площадь сечения должна быть наибольшей, т.е.
2) 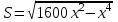 ; ;3) 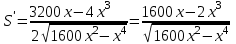 ; ;4) Найдем нули производной: 1600х-2х3=0; х=0 или х= 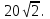 х=0 не удовлетворяет условию задачи. х=0 не удовлетворяет условию задачи. 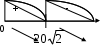 5) Т.К. в точке х= 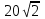 производная функции меняет свой знак с «+» на «-», т в этой точке функция достигает своего максимального значения. производная функции меняет свой знак с «+» на «-», т в этой точке функция достигает своего максимального значения.Ответ: 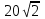 и и 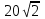 . .№321.
2) 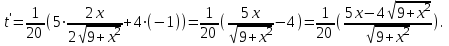 3) Найдем нули производной: 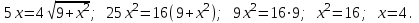  Т.к. в точке х=4 производная функции меняет знак с «- » на «+», то в этой точке функция достигает минимума. Ответ: 4 и 1. Проверка качества (тест). Задание на дом: №313, 316. |

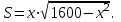

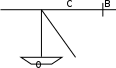
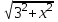 , СВ= 5-х. Т.к.
, СВ= 5-х. Т.к. 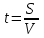 , то
, то