Фрагмент урока математики с использованием ИКТ (Advanced Grapher).. Практическая работа. Урока с использованием информационнокоммуникационных технологий (Advanced Grapher). Предмет алгебра Тема урока Графики функций yax 2 n ya(xm) Класс 9 Цели урока
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Подготовить фрагмент урока с использованием информационно-коммуникационных технологий (Advanced Grapher). Предмет: алгебра Тема урока: Графики функций y=ax2+n y=a(x-m)2. Класс: 9 Цели урока: Рассмотреть параллельный перенос графика функции у=ах2. Задачи: Образовательные: Расширить сведения о свойствах функций. Рассмотреть частные виды квадратичной функции у=ах2+n, у=а(х-m)2, получаемые параллельным переносомграфика функции у=ах2. Сформировать умение строить графики функций у=ах2+n, у=а(х-m)2. Развивающие: Развивать умение обобщать полученные знания. Формировать познавательные умения (наблюдение, сравнение, сопоставление). Развивать умение выдвигать и обосновывать свои высказывания. Повысить эмоциональный настрой учащихся путём привлечения технических средств обучения. Воспитательные: Расширять кругозор учащихся. Воспитывать наблюдательность и внимательность. Вырабатывать навыки социального и делового общения в коллективе. Тип урока: Урок изучения нового материала. Формы работы учащихся: Фронтальная, самостоятельная, индивидуальная. Необходимое техническое оборудование: интерактивная доска, компьютер. На прошлом уроке были рассмотрены два важнейших преобразования графика функции у= х2. График функции у= ах2 получается из графика функции у=х2 растяжением вдоль оси ординат в а раз при а>1 и в 1/а раз при 0<а< 1. Задание 1. Постройте графики функций у=х2, у=1/2х2 и у=2х2. Объясните трансформации, произошедшие с параболой у=х2. 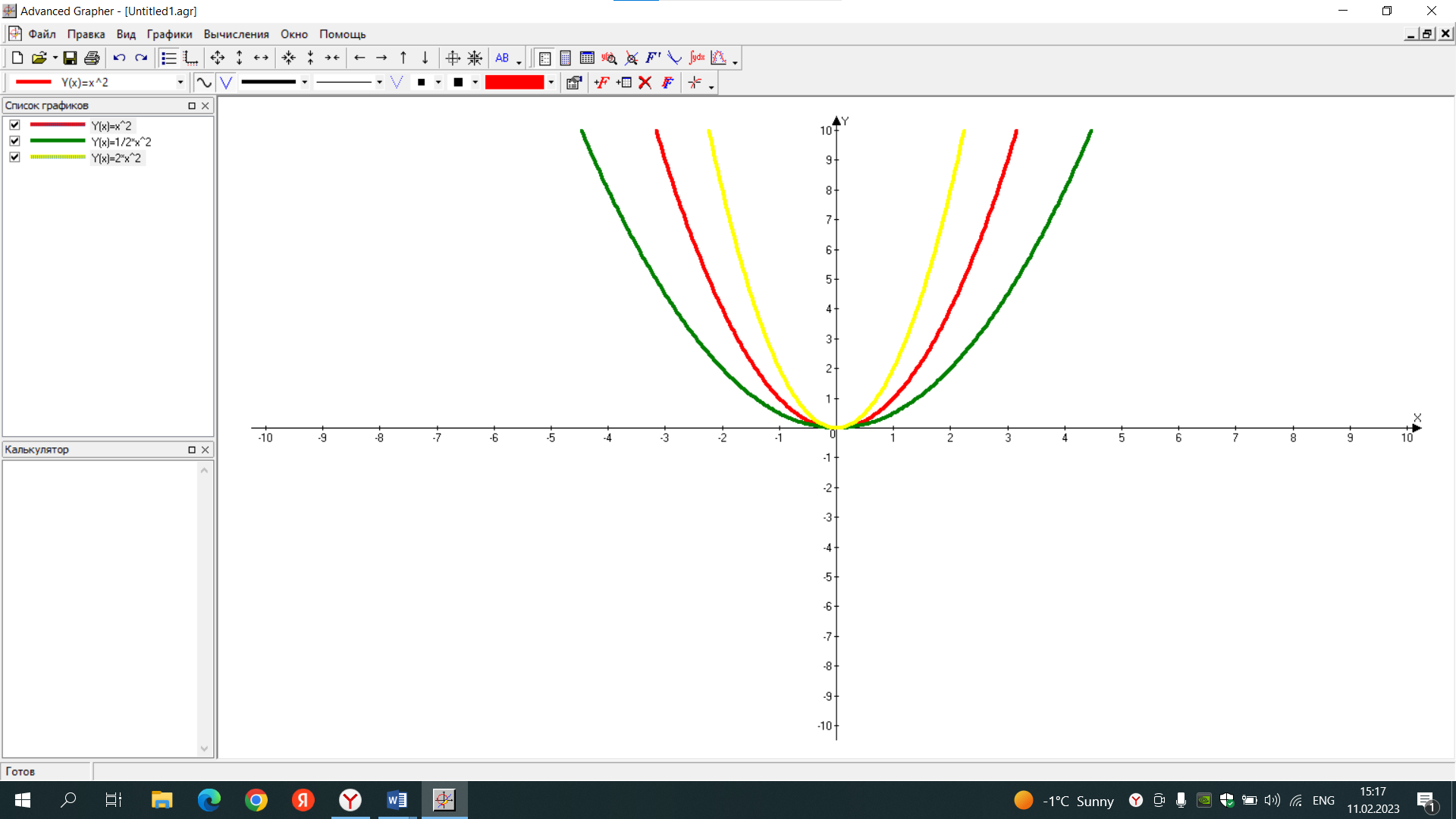 График функции у=-х2 получается из графика функции у=х2 с помощью симметрии относительно оси абсцисс. Задание 2. Постройте графики функций у=х2 и у= -х2. Объясните трансформации, произошедшие с параболой у=х2. 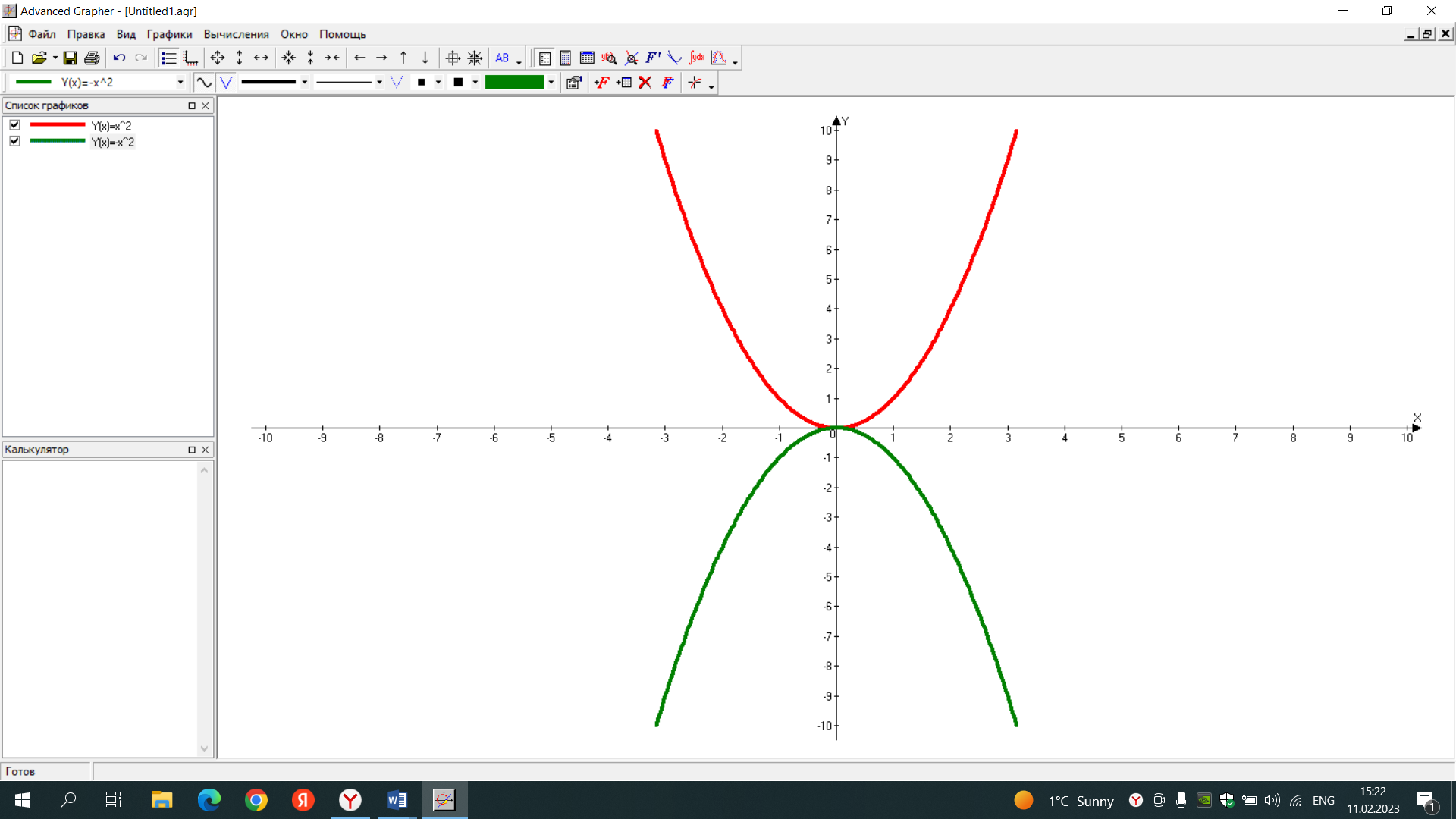 Рассмотрим ещё два важнейших преобразования графика функции у=ах2. Построение графиковфункций у=ах2+n и у=а(х-m)2. График функции у=ах2+n получается из графика функции у=ах2 с помощью параллельного переноса вдоль оси ординат на | n | единиц: вверх при n>0 и вниз при n<0. Задание 3. Постройте график функции у=0,5х2. А затем в этой же системе координат графики у=0,5х2+3 и у=0,5х2-4. С помощью выполнения этого задания можно увидеть, как с помощью параллельного переноса строятся эти графики. Объясните трансформации, произошедшие с параболой у=0,5х2. Назовите координаты вершины каждой параболы.  График функции у=а(х-m)2 получается из графика функции у=ах2 с помощью переноса вдоль оси абсцисс на |m| единиц: вправо при m>0 и влево при m<0. Задание 4. Постройте график функции у=х2. А затем в этой же системе координат графики у=(х-3)2, у=(х+4)2, у=0,5(х-5)2, у=0,5(х+2)2. С помощью выполнения этого задания можно увидеть, как с помощью параллельного переноса строятся эти графики. Объясните трансформации, произошедшие с параболой у=х2. Объясните трансформации, произошедшие с параболами у=х2 и у= 0,5х2. Назовите координаты вершины каждой параболы. 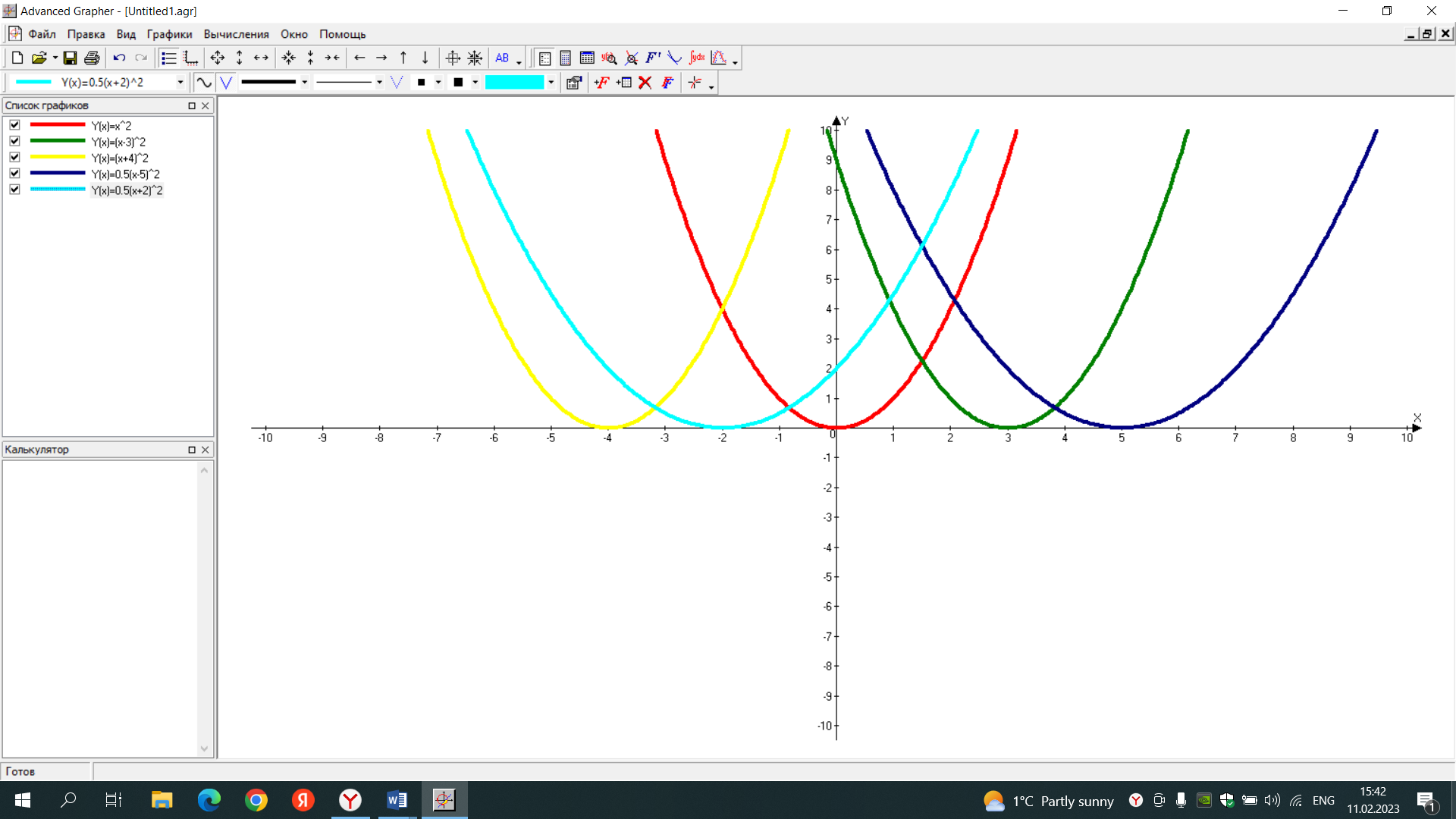 Задание 5. В одной системе координат построить графики функций у=2х2, у= -2(х+2)2, у= -2х2, у= -2(х-4)2. Объясните трансформации, произошедшие с параболой у=2х2. Назовите координаты вершины каждой параболы. Назовите координаты вершины каждой параболы. 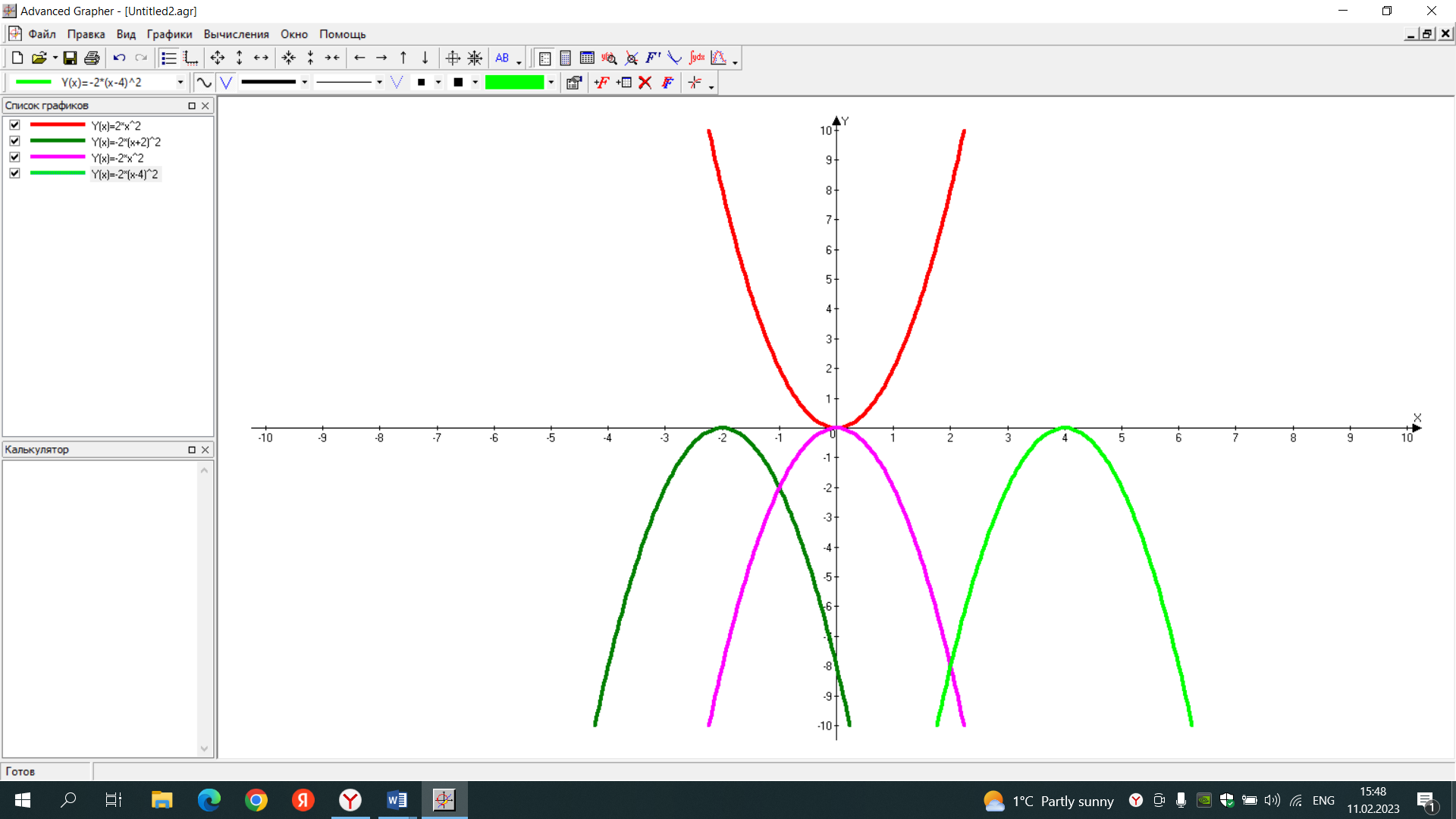 |
