Условие устойчивость Михайлова
|
Все n корней должны быть левыми
|
Критерий Найквиста работает по
|
АФЧХ (амплитудно-фазовой частотной характеристике)
|
Частотные критерии
|
Михайлова, Найквиста
|
Алгебраические критерии не работают, когда …
|
|
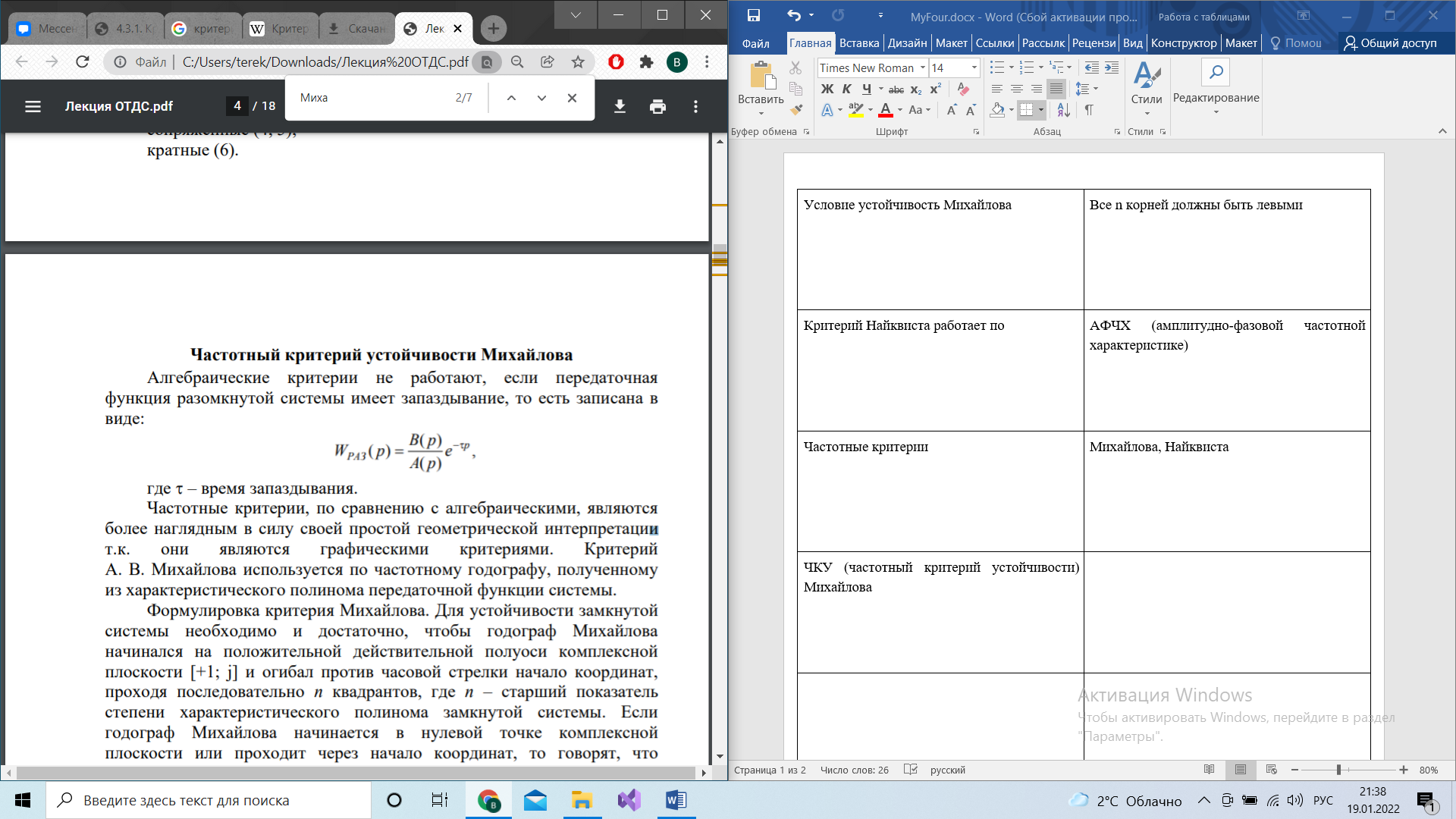
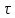 в ЧКУ Михайлова – это …
|
Время запаздывания
|
ЧКУ Михайлова определяет
|
Частотный годограф
|
Формулировка критерия Михайлова
|
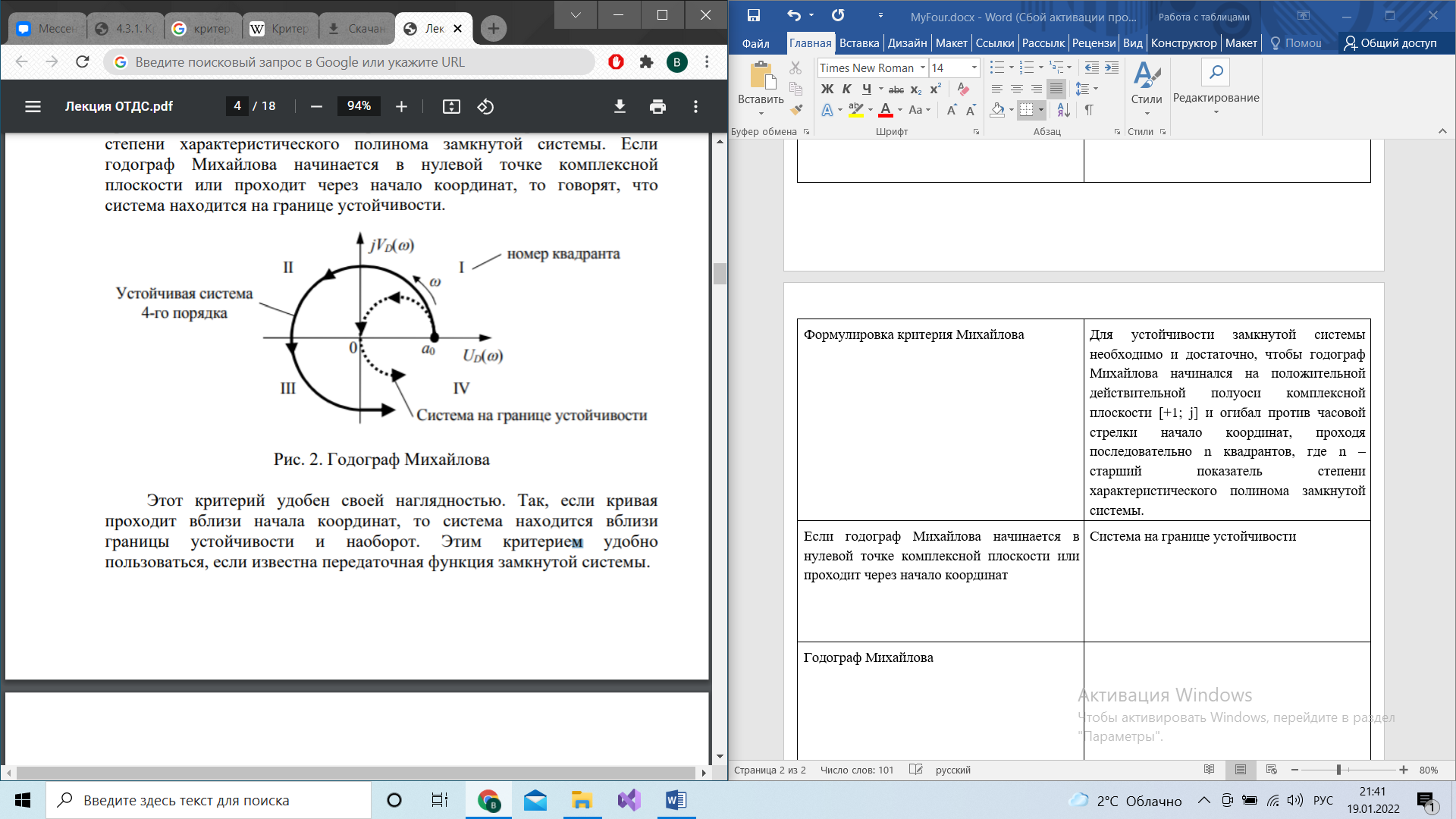
Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Михайлова начинался на положительной действительной полуоси комплексной плоскости [+1; j] и огибал против часовой стрелки начало координат, проходя последовательно n квадрантов, где n – старший показатель степени характеристического полинома замкнутой системы.
|
Если годограф Михайлова начинается в нулевой точке комплексной плоскости или проходит через начало координат
|
Система на границе устойчивости
|
Годограф Михайлова
|
|
Формулировка критерия Найквиста
|
Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы на комплексной плоскости [+1; j] (рис. 3.3) при изменении частоты от 0 до ∞ не охватывала точку с координатами (–1; j0).
|
(Найквист) Если АФЧХ разомкнутой системы проходит через точку с координатами (–1; j0), то система находится …
|
На границе устойчивости
|
Скачать 0.94 Mb.