задача нелинейного программирования. Условие задачи Построить область допустимых планов

• Название: Условие задачи 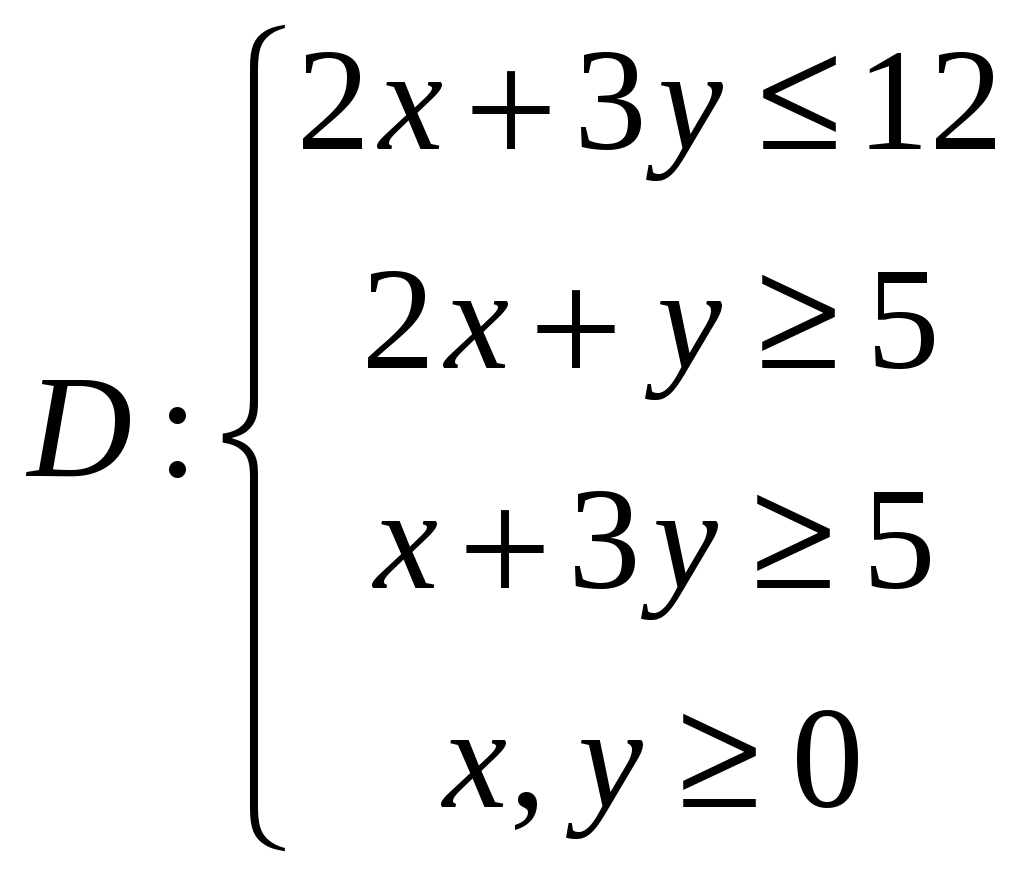Построить область допустимых планов
• Анкор: задача нелинейного программирования
• Дата: 27.05.2022
• Размер: 243.5 Kb.
• Имя файла: задача нелинейного программирования.doc
• Тип: Документы; #552287

Условие задачи:

1. 
   Построить область допустимых планов D и линии уровня целевой функции, решить задачи геометрически. Исследовать целевую функцию на выпуклость (вогнутость).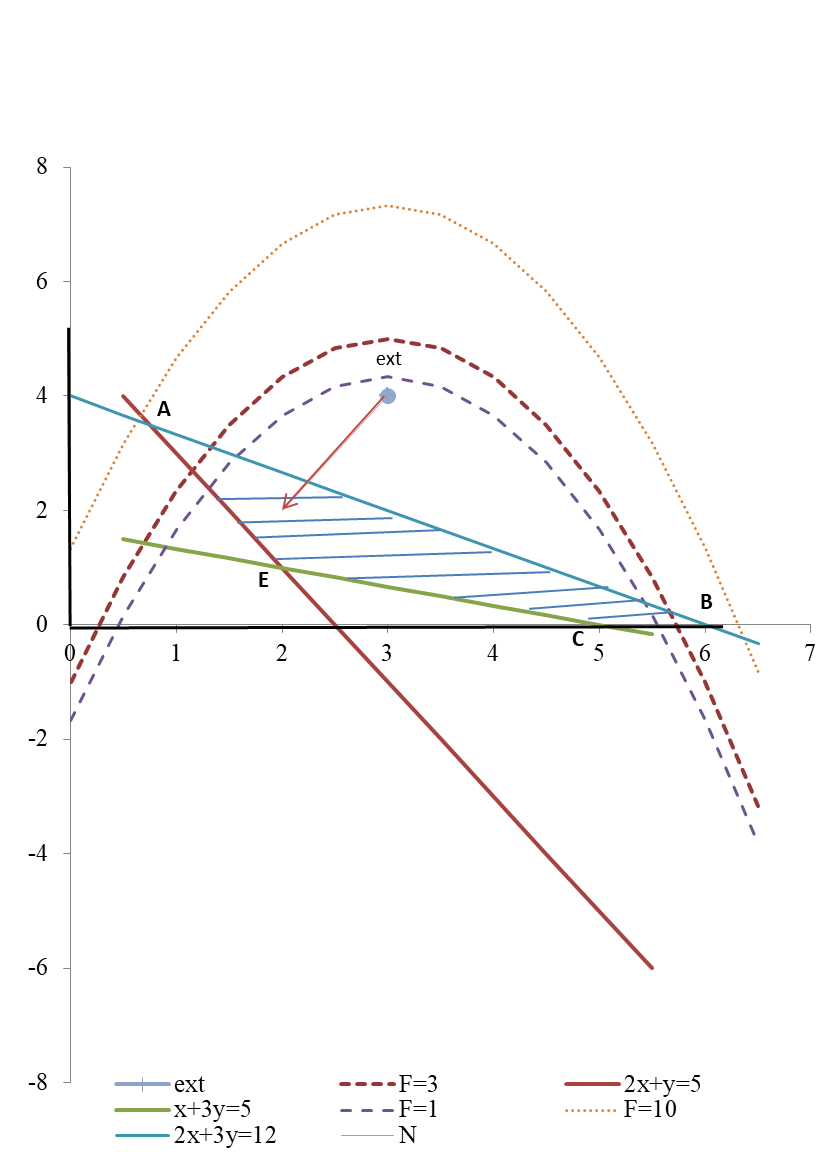
   

Рисунок - Область допустимых планов D = АВСЕ и линии уровня целевой функции: F=1, F=3 и F=10.
С(5, 0); В(6, 0); ;



- max

- min



Найдем частные производные: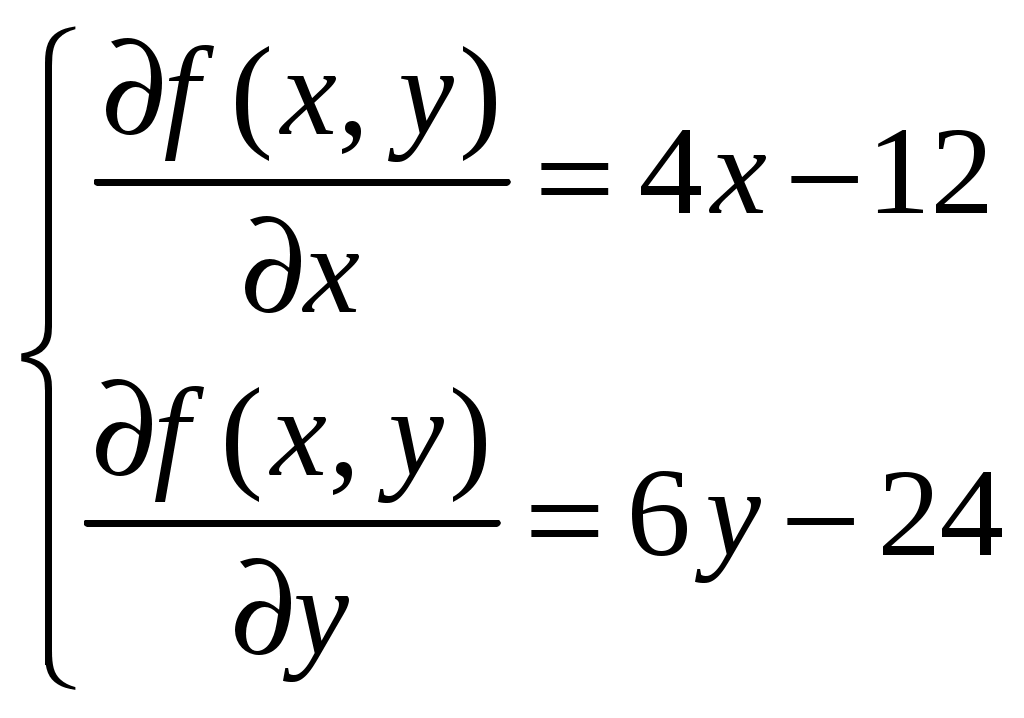

- вектор роста функции

Решим систему уравнений:



Количество стационарных точек равно 1: M(3;4)

Найдем частные производные второго порядка: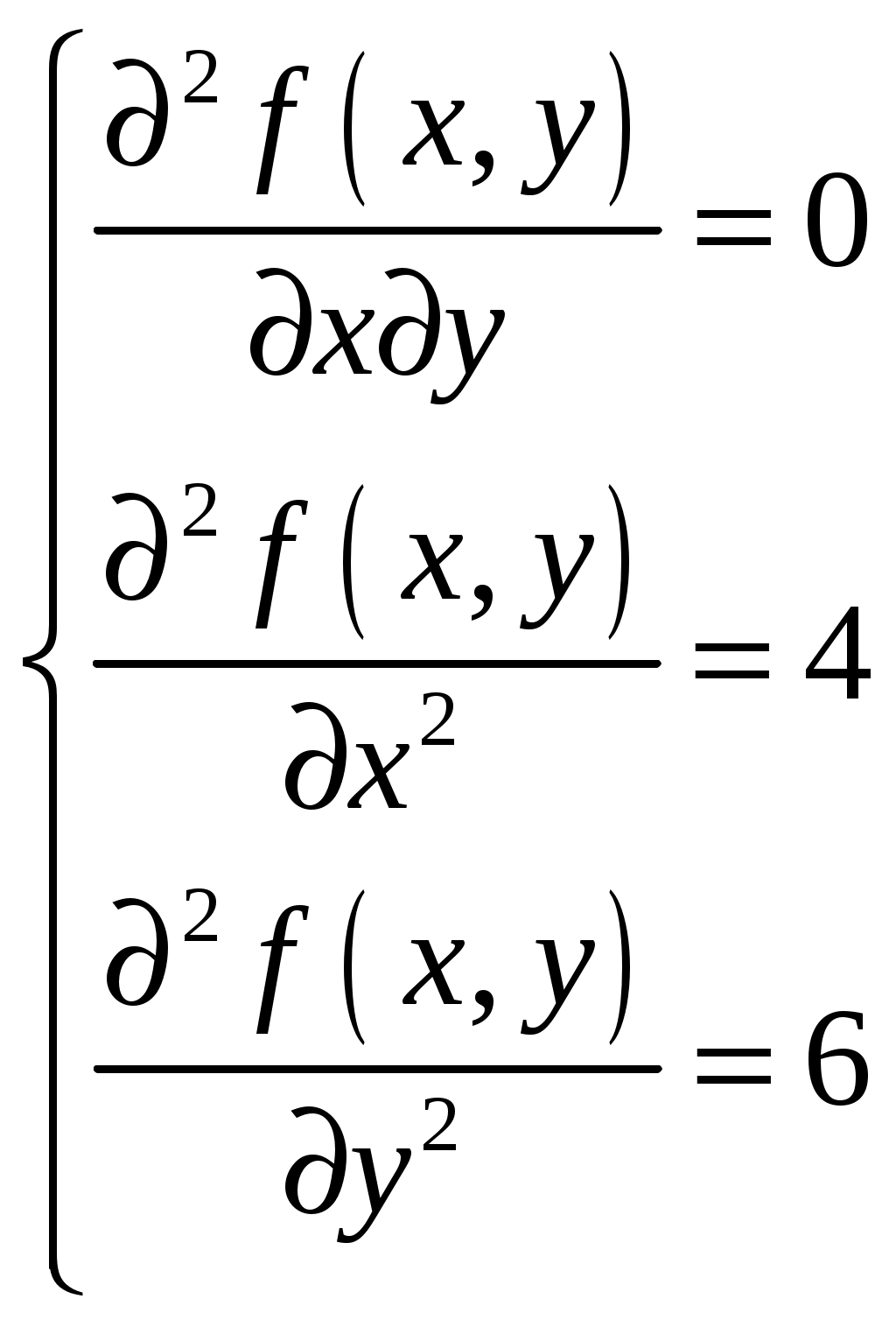



Вычисляем значения для точки M(3;4)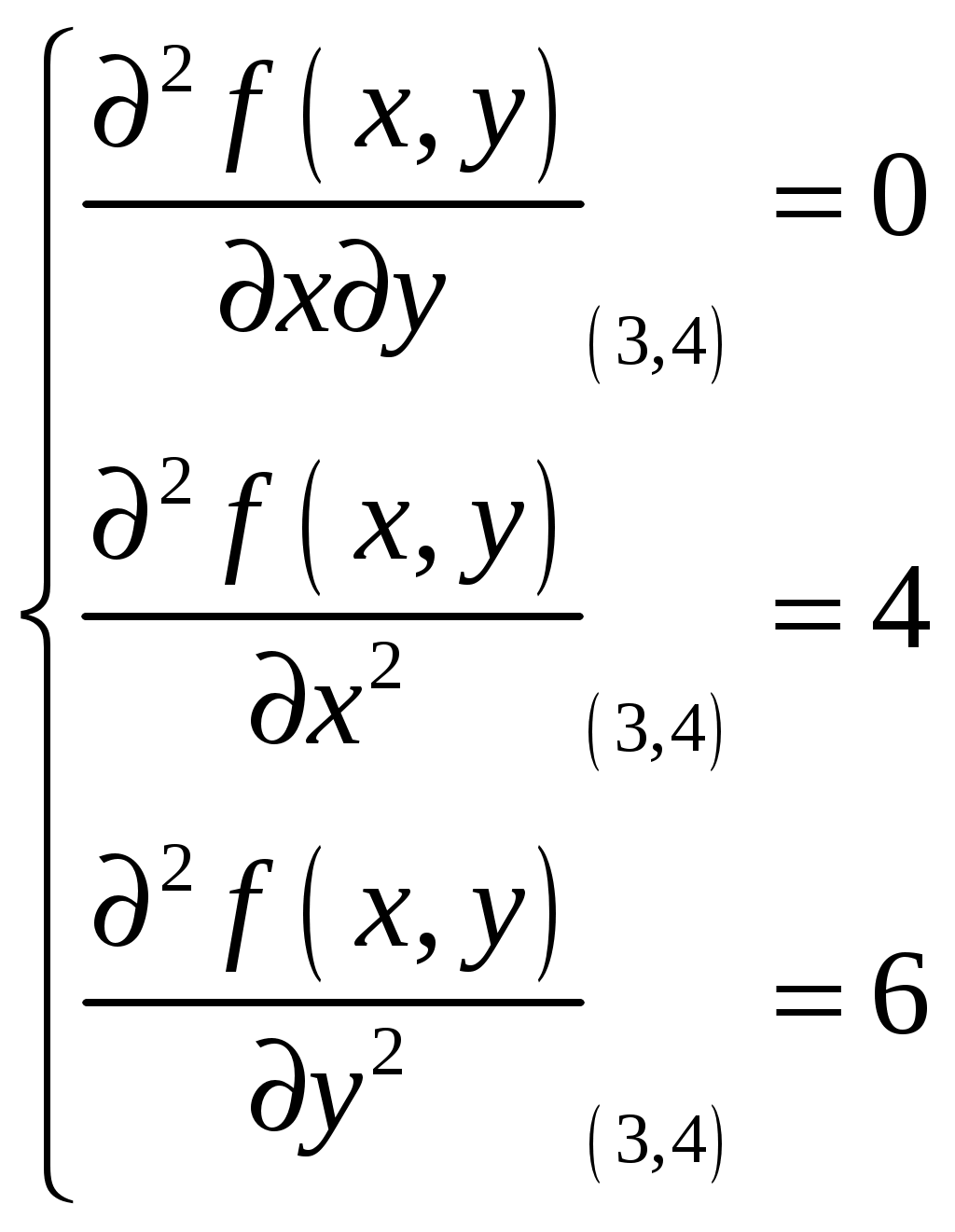



Строим матрицу Гессе:

D₁ = a₁₁ > 0, D₂ = 24 > 0

В точке M(3;4) матрица Гессе положительно определена, и функция является выпуклой. Точка (3;4) является точкой минимума, но не принадлежит области D.

2. 
   Составить функции Лагранжа для задачи минимизации целевой функции. Проверить необходимые условия Куна-Таккера для экстремальной точки, а также достаточные условия.
   

Перепишем ограничение задачи в неявном виде:

φ₁(x,y) = (2x+3y) – 12 = 0

φ₂(x,y) = 5-(2x+y) = 0

φ₃(x,y) = 5-(x+3y) = 0

Составим вспомогательную функцию Лагранжа: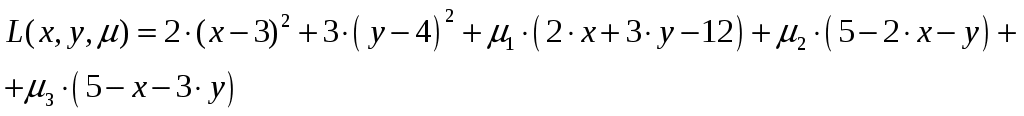



Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным х_i и неопределенным множителям μ_i.

Составим систему:











Проверим необходимые условия Куна-Таккера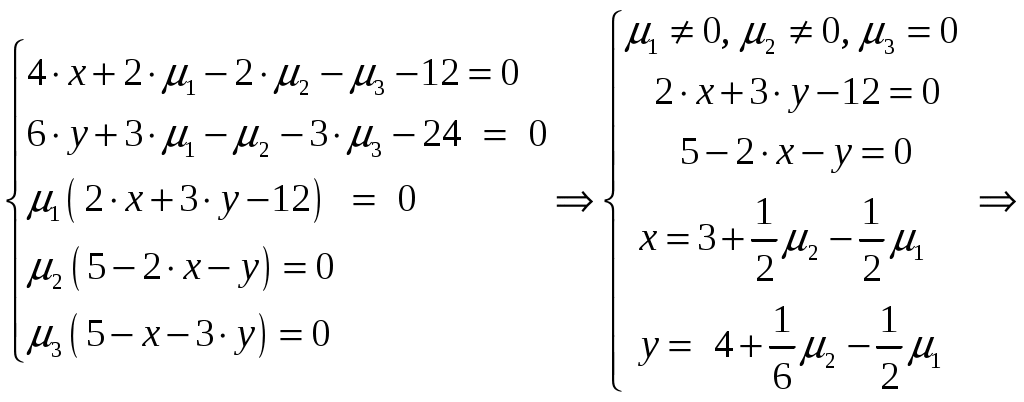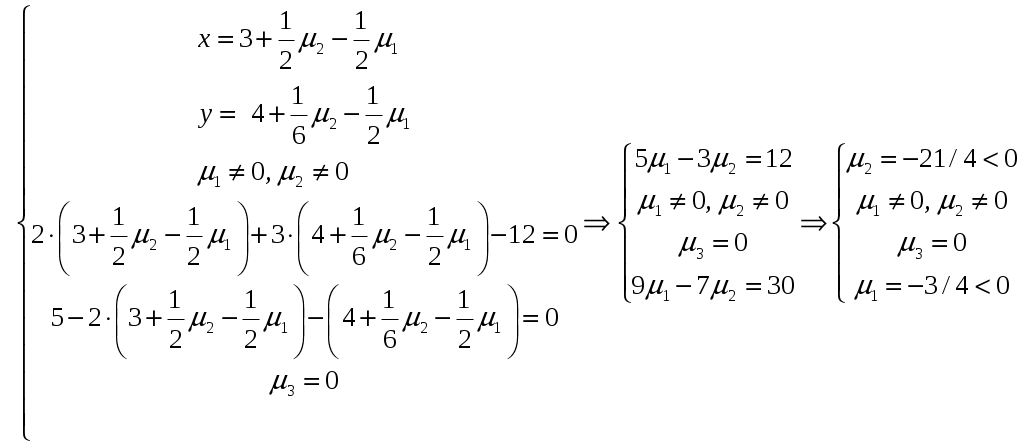





Не выполняются условия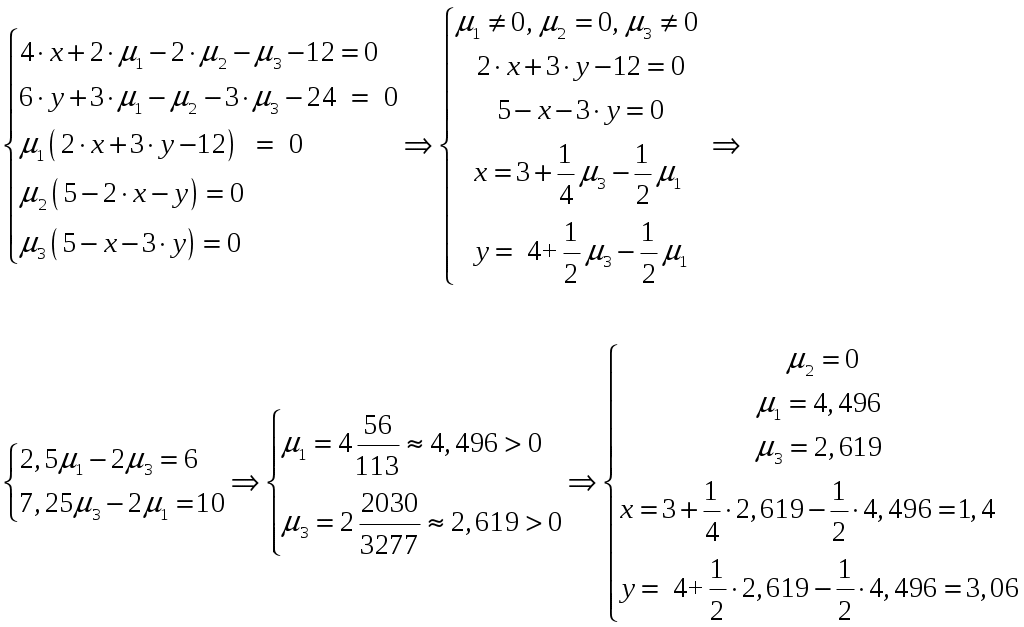



X=(1,4;3,06;4,496;0;2,619)

точка (1,4; 3,06) – точка условного минимума, который равен -6,93
3. Составить функции Лагранжа для задачи максимизации целевой функции. Проверить необходимые условия Куна-Таккера для крайних точек множества допустимых планов.

L(x,y,μ_i) = 2(x-3)²+3(y-4)² -μ₁(12-(2x+3y))-μ₂(5-(2x+y))-μ₃(5-(x+3y)) max

Составим систему:

1. 
   Для С(5,0) не выполняется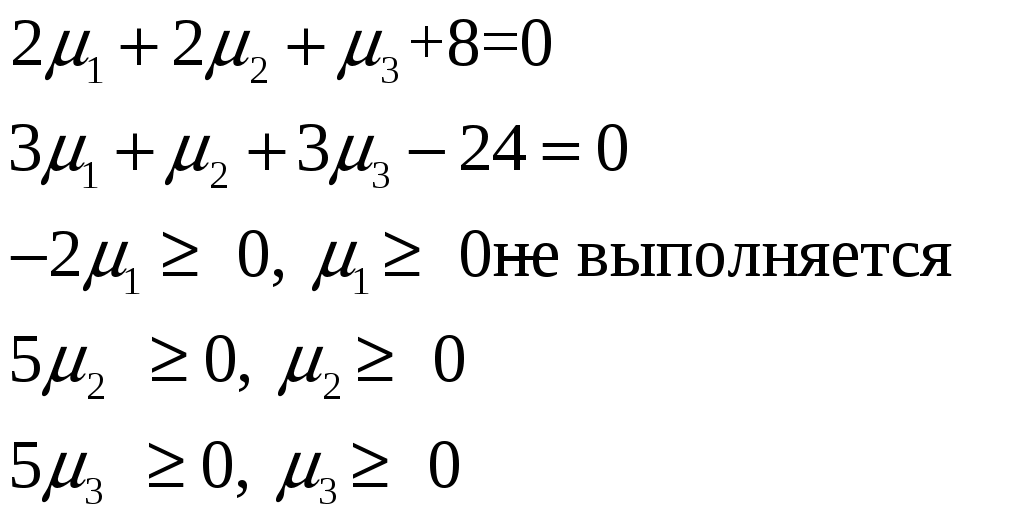
   

2. 
   Для Е(2,1) не выполняется
   

противоречие

3. 
   В(6,0) – не выполняется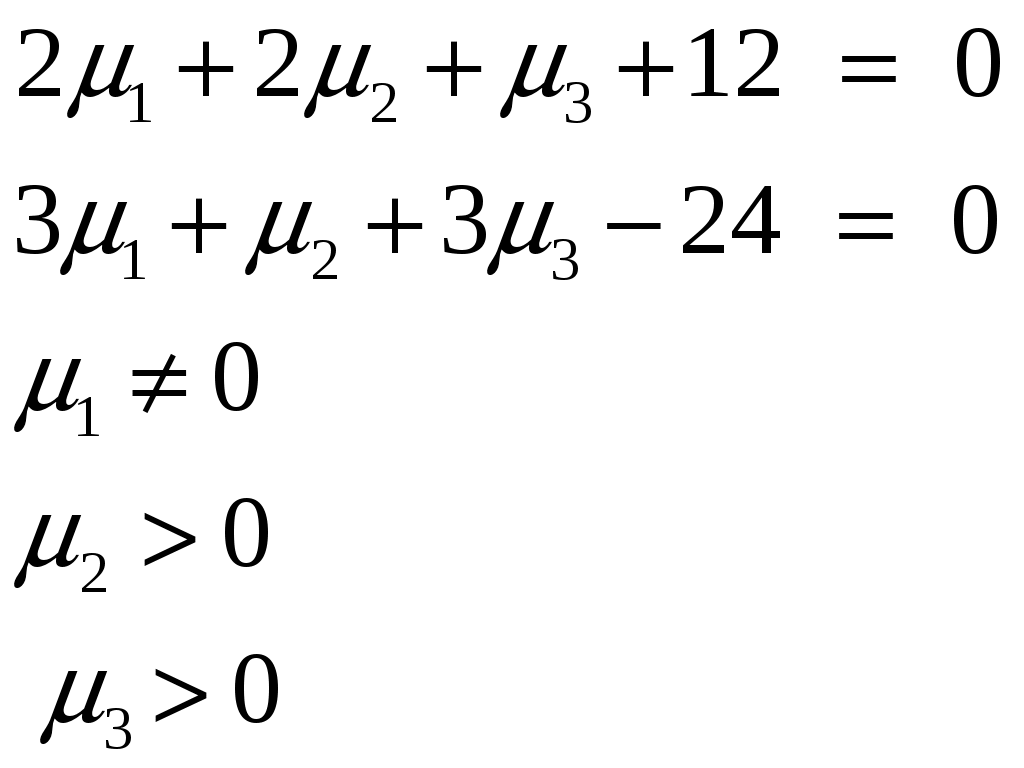
   

Если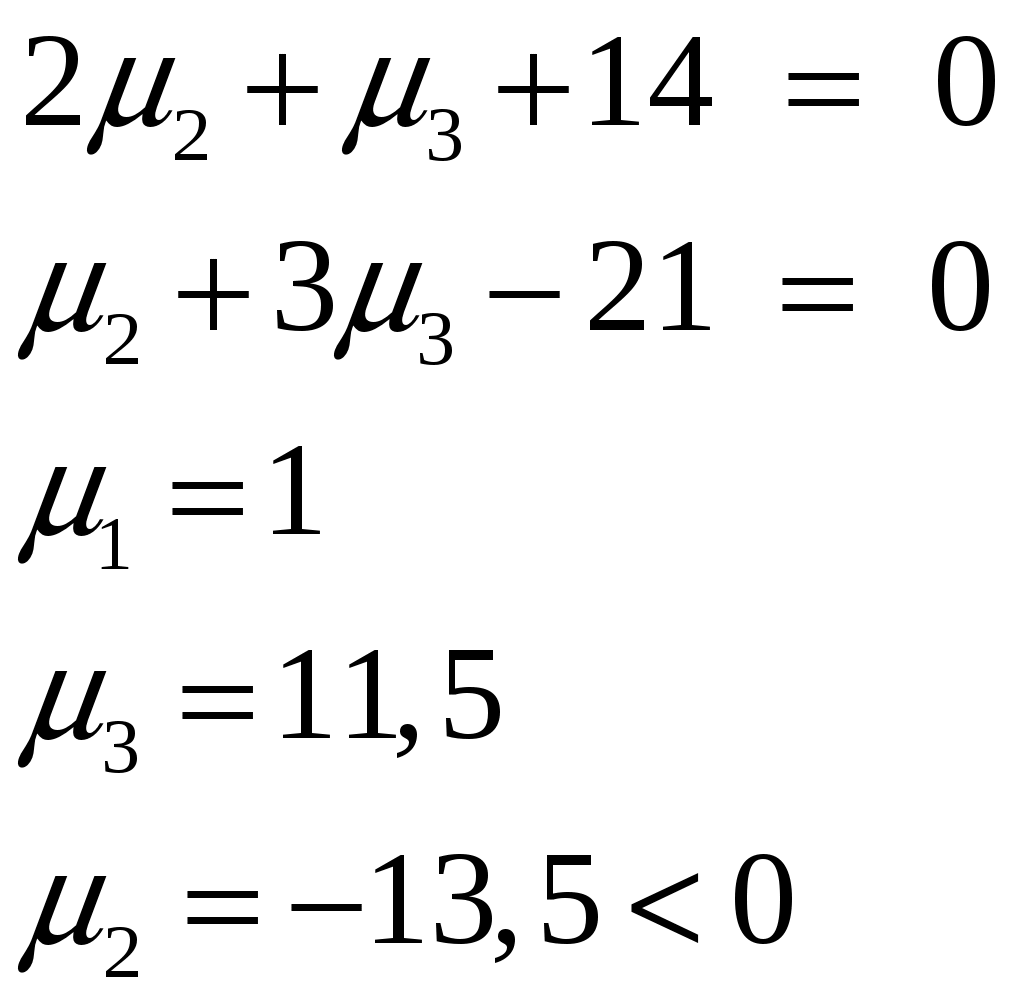



Для точки А(0,75; 3,5).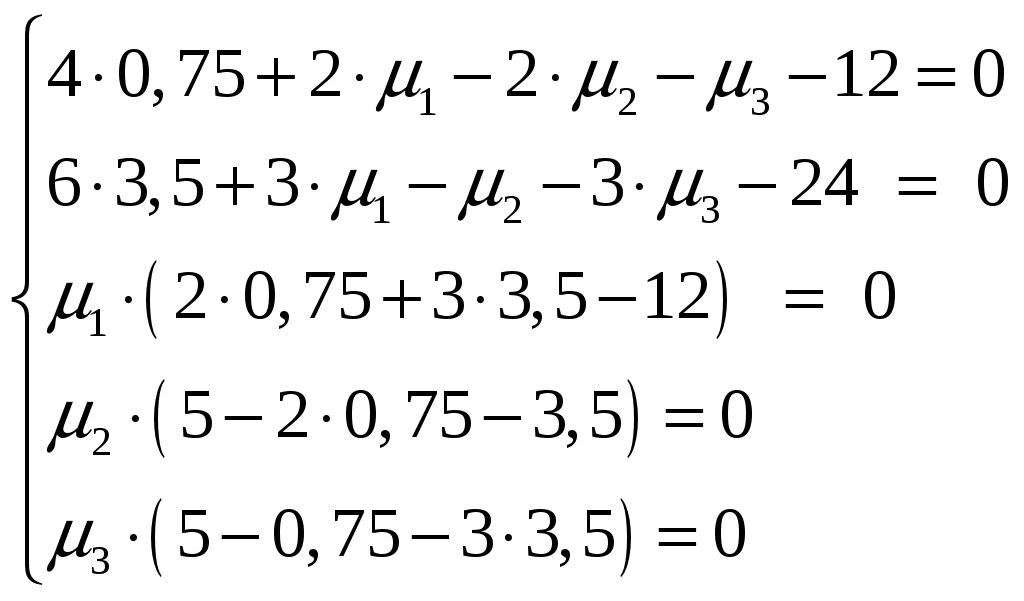



Пусть μ₃ = 0, μ₁ ≠ 0 и μ₂ ≠ 0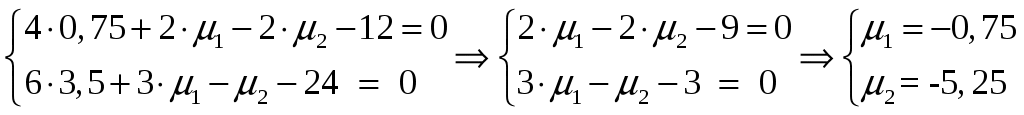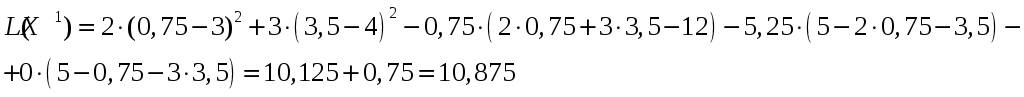







А(0,75; 3,5) точка условного максимума.

Максимальное значение составит L_max=10,875

4. 
   Определить экстремумы функции f(x₁; x₂) с помощью надстройки «Поиск решений» программы ExcelMSOffice взяв за начальные приближения крайние точки множества D (привести сообщения о завершении работы надстройки в обоих случаях).
   

	max		min
F(x,y)=	10,875		7,2
	переменные
х	y		х	y
0,75	3,5		1,8	2,8
	ограничения
12	12	<=	12
5	6,4	>=	5
11,25	10,2	>=	5
3,5	1,8	>=	0
0,75	2,8	>=	0

Максимум достигается в точке А(0,75;3,5) и равен

Минимум достигается в точке Р(1,8; 2,8) и равен