Задания. Условие задания
 Скачать 236.39 Kb. Скачать 236.39 Kb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Институт финансов, экономики и управления (наименование института полностью) Департамент бакалавриата (наименование кафедры/департамента/центра полностью) 38.03.03 Управление персоналом (код и наименование направления подготовки, специальности) Управление персоналом (направленность (профиль) / специализация) ПРАКТИЧЕСКИЕ ЗАДАНИЯ по учебному курсу «Финансовые вычисления» (наименование учебного курса)
Тольятти 2023 Практическое задание 1Условие заданияПостоянные издержки F, не зависящие от числа произведенной продукции х, составляют 135 тыс. руб. в месяц, а переменные издержки V – 750 руб. на каждую единицу продукции. Цена единицы продукции – 1300 руб. Найдите объем продукции х, при котором прибыль П равна 115 тыс. руб.Решение Для определения объема продукции х необходимо построить линейное уравнение, увязывающее в зависимость приведенные в условии задачи показатели. При этом: выручка представляет собой общий объем произведенной и реализованной продукции и определяется как произведение стоимости единицы продукции и общего объема произведенной продукции в натуральном выражении; общая сумма затрат складывается из затрат постоянных и затрат переменных. Последние, в свою очередь, определяются как произведение суммы затрат, приходящейся на единицу произведенной продукции, и общего объема произведенной продукции в натуральном выражении; прибыль (П) = выручка (В) – затраты (З). Для расчёта воспользуемся формулой сложных процентов. S = P*(1+j/m)^mn m – число начислений в год n – количество лет j – процентная ставка P — изначальная сумма Вариант 1: F = 100 000 * (1 + 0,15/1) 1*1 = 115 000 Вариант 2: F = 150 000 * (1 + 0,11/4) 4*2 = 186 357 Вариант 3: F = 120 000 * (1 + 0,12/2) 2*1,5 = 142 921 Вариант 4: F = 300 000 * (1 + 0,085/12) 12*1 = 326 517 Вариант 5: F = 120 000 * (1 + 0,09/12) 12*1,5 = 131 256 Вариант 6: F = 90 000 * (1 + 0,095/12) 12*1 = 98 932 Вариант 7: F = 110 000 * (1 + 0,118/2) 2*1 = 123 362 Вариант 8: F = 100 000 * (1 + 0,12/4) 4*2 = 126 677 Вариант 9: F = 90 000 * (1 + 0,121/4) 4*1,5 = 104 461 Вариант 10: F = 115 000 * (1 + 0,16/1) 1*1 = 133 400
Вывод: Расчет в таблице показал, что наибольшее количество процентных денег будет получено по варианту 2. Практическое задание 2Условие заданияСебестоимость производства телевизоров 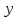 (в тыс. руб.) описывается функцией (в тыс. руб.) описывается функцией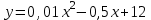 , где , где 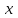 – объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед. – объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед.Решение1. Для решения задания воспользуйтесь следующим алгоритмом. Для определения функции скорости изменения себестоимости найдите первую производную от заданной в условии функции. Для определения функции темпа изменения себестоимости найдите вторую производную от заданной в условии функции. Подставьте в полученные функции заданные в условии объемы выпуска продукции. 2. Сделайте вывод. Практическое задание 3Тема 7. Экономико-математическое моделированиеУсловие задания. Провести процедуру краткосрочного прогнозирования спроса на некоторую услугу (млн руб.), используя процедуру сглаживания (по пяти точкам).
Рекомендации по выполнению задания Решение задания следует произвести на основе представленного в бланке выполнения задания 3 алгоритма. Бланк выполнения задания 3Условие задания. Проведите процедуру краткосрочного прогнозирования спроса на некоторую услугу (млн руб.), используя процедуру сглаживания (по пяти точкам) на основе данных, указанных в таблице.
Решение1. Для решения задачи используйте следующие формулы: 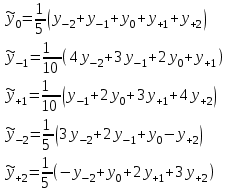 Первая формула позволяет определить сглаженные значения всех средних точек ряда (с 3-й по 10-ю), а оставшиеся формулы соответственно направлены на сглаживание крайних точек ряда (т. е. 2-й, 11-й, 1-й, 12-й точек соответственно). 2. Изобразите полученные результаты графически. Для этого в системе координат по оси 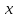 отложите порядковые номера месяцев, а по оси отложите порядковые номера месяцев, а по оси 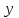 – объем спроса с удобным для вас шагом. В полученной системе координат постройте два графика: первый – по фактическим значениям, представленным в условии, второй – по значениям, полученным в результате проведенных расчетов. – объем спроса с удобным для вас шагом. В полученной системе координат постройте два графика: первый – по фактическим значениям, представленным в условии, второй – по значениям, полученным в результате проведенных расчетов.Практическое задание 4Тема 7. Экономико-математическое моделированиеУсловие задания. Рассчитать прогнозное значение по методу ЭВС на основе данных, приведенных в таблице с шагом прогнозирования, равным 1, и начальной оценкой U0 = 15. Расчеты следует провести при α = 0,2 и α = 0,3.
Рекомендации по выполнению заданияРешение задания следует произвести на основе представленного в бланке выполнения задания 4 алгоритма. Бланк выполнения задания 4Условие задания. Рассчитать прогнозное значение, используя метод экспоненциально взвешенного среднего (ЭВС) на основе данных, приведенных в таблице, с шагом прогнозирования, равным 1, и начальной прогнозной оценкой U0 = 15. Расчеты следует провести при α = 0,2 и α = 0,3.
Решение задания При сглаживании временного ряда методом ЭВС используется следующая формула: 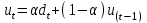 , ,где 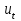 – прогнозное значение ЭВС; – прогнозное значение ЭВС; 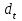 – фактическое значение показателей в момент t; – фактическое значение показателей в момент t; 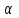 – параметр сглаживания; t – номер текущего периода; – параметр сглаживания; t – номер текущего периода; 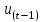 – прогнозное значение показателей в момент t. – прогнозное значение показателей в момент t.Практическое задание 5Тема 7. Экономико-математическое моделированиеУсловие задания. Имеется четыре измерения пары переменных |
| х | 1 | 2 | 3 | 4 |
| у | 0,2 | 0,3 | 1,0 | 1,2 |
Методом наименьших квадратов постройте линейную зависимость
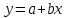 .
.Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 5 алгоритма.
Бланк выполнения задания 5
Условие задания. Имеется четыре измерения пары переменных
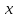 и
и 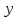 , результаты которых приведены в таблице:
, результаты которых приведены в таблице:| х | 1 | 2 | 3 | 4 |
| у | 0,2 | 0,3 | 1,0 | 1,2 |
Методом наименьших квадратов постройте линейную зависимость
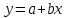 .
.Решение
Метод наименьших квадратов позволяет представить линейное уравнение вида
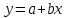 в виде системы уравнений:
в виде системы уравнений: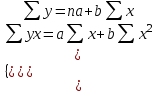 .
.Для того чтобы найти значения параметров линейного уравнения
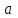 и
и 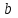 , следует произвести расчет всех известных составляющих системы. Для упрощения расчетов воспользуйтесь таблицей:
, следует произвести расчет всех известных составляющих системы. Для упрощения расчетов воспользуйтесь таблицей: 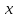 | 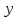 | 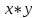 | 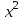 |
| 1 | 0,2 | ? | ? |
| 2 | 0,3 | ? | ? |
| 3 | 1,0 | ? | ? |
| 4 | 1,2 | ? | ? |
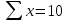 | 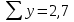 | 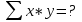 | 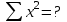 |
Рассчитав все неизвестные в таблице значения, подставьте их суммарные значения в систему уравнений и решите ее. В ответе укажите значения параметров
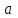 и
и 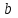 и впишите полученные значения в исходное уравнение вида
и впишите полученные значения в исходное уравнение вида 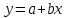 .
.Практическое задание 6
Тема 8. Теория игр
Условие задания. На основе квартальных данных об объемах продаж продукции предприятия (тыс. шт.) за 5 лет построена экономико-математическая модель. Оценки коэффициентов сезонности за последний год представлены в таблице.
| Квартал | 1 | 2 | 3 | 4 |
| Коэффициент сезонности | 0,89 | 1,15 | 1,25 | 0,71 |
Рассчитайте прогнозную оценку уровня продаж в I полугодии следующего года, если уравнение тренда имеет вид
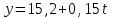 .
.Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 6 алгоритма.
Бланк выполнения задания 6
Условие задания. На основе квартальных данных об объемах продаж продукции предприятия (тыс. шт.) за 5 лет построена экономико-математическая модель. Оценки коэффициентов сезонности за последний год представлены в таблице.
| Квартал | 1 | 2 | 3 | 4 |
| Коэффициент сезонности | 0,89 | 1,15 | 1,25 | 0,71 |
Рассчитайте прогнозную оценку уровня продаж в I и II полугодиях следующего года, если уравнение тренда имеет вид
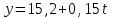 .
.Решение
Прогнозная оценка уровня продаж осуществляется на основе использования заданной в условии задачи экономико-математической модели посредством подстановки в уравнение порядковых номеров полугодий, следующих за порядковыми номерами временных интервалов, указанных в таблице.
