емтихан. Устемирова Ботакоз Рунге Кутт дісі
 Скачать 144.97 Kb. Скачать 144.97 Kb.
|
|
Устемирова Ботакоз Рунге – Кутт әдісі Жауабы: Рунге – Кутт әдісі бул әдіс функцияның мәндерін іздеп есептерді тізбегін есептеу формуласы мен бул жердегі нуктелердің тендеуіндегі жауабы болып табылады. Рунге Кутт әдістерінің басқа да бірреттік әдістері бар болып табылады. Олар k=1, y мәндерімен шыгарылады. Осы әдістердің ішіндегі ен коп тараган осы Рунге Кутт әдісі болып табылады. Осы әдіс турлі далдік катардың айырмалы сызбаларынан тургызылады. Осы Рунге Кутт әдісінің коп колданылатын формуласы  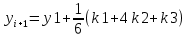 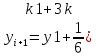 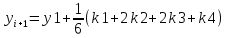 Осы формулага карап отырып Рунге Кутт әдісінің алгоритімін крастырып кореиік 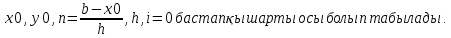 X0,y0, есептелген мәндерін корытындылау K1,k2, k3,k4 есепту Рунге Кутт әдісі коптеген есептеуді есептеу лер кажет етеді және де әдістер ділелдікке ие болгандықтан есептерді шыгаруга мумкіндіктер береді. Бул әдістің артықшылыгы аиналым кадамы мен мумкіндігі сонымен бірге біркелкі есептерді жургізуге болады. Рунге Кутт әдісі Xi – 0. 0.05 0.1 0.15 Yi-1 1.0477 1.0912 1.1341 Осылаиша Рунге Кутт әдісі жалгасын таба береді. 2 Ен кіші квадраттар әдісі бул әдіс функциялардың кесетелік турде берілуінен кенінен тараган турі болып табылады. Бул квадратты әдіс кестелік мінездеме турінде кездесіп жатады. Және де кестелік функцияларда мәндік бейнелеу корсетип кана коимаи аинымалы шамалар арасында анықтамалар да корсетип отырады. Ен кіші квадарттар әдісі аинымалы лар біркелкі турде корсетуге бола береді жіне де кіші квадарттар әдісі мен және фунциялар мәндік туред жаксы корінеді. Y=f(x) функиясын мәндер ретінде корсетип кореиік Y1= f(x), j=0,1,2,3,….,n Xj. x0 .x1 . x2,..,xn Yj . y0. Y1.y2. …yn Бул функциялар алгебарда кобінесе кездесетин болгандықтан оларды ен кіщі квадраттық әдістер ретінде де колданылады. Казіргі танда бул математикалық есептерді коп жерлерде кездестіруге болады. Жогаргы оку орындарында коп кездесіп жатады. Бул әдістердің көбінесе казакша окулықтарды коп кездесе бермеиді. Бул әдістерді уирену ушін коп ізденістер керек болады. Ен кіші кавдраттар әдісін колдануда кызыкты жазылган кітаптар бар екекін білесіздер. Онын мәні кыскаша аитканда ен кіші квадраттар әдісі олшеу нәтижесін белгісіз шамалар багасын беру ушін ен ынгаилы арі тиімді әдіс болып табылады. Бул жагдаилар неше турлу жагдаига акеп согу мумкін. 90/11=8.18теңдігінің абсолюттік қателігін табыңыз. 90/11=8,18 (8.18-8)=0,18 0.18/8=0,0225 0,0225*100%=2,25% |
