УЗЛОВОЙ И КОНТУРНЫЙ АНАЛИЗ И ПРЕОБРАЗОВАНИЕ ЭЛЛЕКТРИЧЕСКИХ ЦЕПЕЙ. курсач3. Узловой и контурный анализ и преобразование эллектрических цепей курсовая работа
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «Дальневосточный федеральный университет» ШКОЛА ПЕДАГОГИКИ Кафедра математики, физики и методики преподавания Цыганок Анна Витальевна УЗЛОВОЙ И КОНТУРНЫЙ АНАЛИЗ И ПРЕОБРАЗОВАНИЕ ЭЛЛЕКТРИЧЕСКИХ ЦЕПЕЙ КУРСОВАЯ РАБОТА
г. Уссурийск 2018 г. Оглавление Введение 3 Метод контурных токов 6 Метод узловых потенциалов 11 Заключение 14 Список использованных источников 15 ВведениеРеальные электротехнические устройства и системы имеют сложные схемы. В электрические цепи, кроме основных элементов – источников и приемников электрической энергии, входят различные вспомогательные аппараты и приборы, предназначенные для управления (рубильники, переключатели), регулирования (реостаты, стабилизаторы тока и напряжения), защиты (плавкие предохранители, реле), контроля (амперметры, вольтметры и другие электроизмерительные приборы). Перед специалистами стоят задачи расчета их параметров. Процесс расчета параметров в теории электротехники принято называть «анализом схем». Электрические схемы любой сложности подчиняются законам Ома и Кирхгофа. Однако применение только этих законов часто приводит к неоправданно сложным решениям. Поэтому был разработан ряд методов анализа, адаптированных к технологи электрических цепей и упрощающих процесс расчета их параметров. Основной задачей анализа электрических цепей является определение токов всех ветвей при заданной конфигурации цепи и известных параметрах всех ее элементов. При расчете токов часто изображают не реальную цепь, а ее схему замещения. Схема замещения - это графическое изображение реальной цепи с помощью идеальных элементов, параметрами которых являются параметры реальных элементов, входящих в цепь.[1] На схеме замещения не указывают измерительные приборы, аппаратуру защиты и аппаратуру включения-выключения. На схеме замещения различают ветви, узлы и контуры. Ветвь - это участок цепи, в любом сечении которого течет один и тот же ток. Узел - это точка, в которой сходится не менее трех ветвей. Контур - любой замкнутый путь для электрического тока. [2] Контур называется независимым, если он имеет хотя бы один элемент, принадлежащий только ему. Элементы цепи могут включаться последовательно и параллельно. При последовательном включении во всех элементах протекает один и тот же ток. При параллельном включении элементы цепи подключаются к одной паре узлов. Для расчета токов в ветвях цепи применяют законы Кирхгофа и Ома. Первый закон Кирхгофа [3] относится к узлу и гласит: алгебраическая сумма токов, сходящихся в узле, равна нулю. где i - номер тока; n - количество токов, сходящихся в узле. Второй закон Кирхгофа [3] относится к контуру, он гласит: Алгебраическая сумма ЭДС, действующих в контуре, равна алгебраической сумме падений напряжений в том же контуре. где i - номер ветви контура; n - число ветвей, входящих в контур. Законы Кирхгофа применяют для расчета сложных разветвленных цепей, включающих в себя несколько источников энергии. При этом необходимо составить N = Nв –(Nу-1) уравнений, где Nв - число ветвей, Nу - число узлов. При расчете рекомендуется придерживаться следующей последовательности: [4] Выбрать направление обхода контуров (ошибок в дальнейшем будет меньше, если направление будет во всех контурах одинаковым). Произвольно указать направление токов в ветвях цепи. Составить необходимые уравнения по первому закону Кирхгофа. Составить необходимые уравнения по второму закону Кирхгофа, считая положительными токи и ЭДС, совпадающие с направлением обхода контура. Решить полученную систему уравнений любым известным методом. Провести проверку правильности решения путем составления баланса мощностей. В данной работе я рассмотрю следующие основные методы анализа простейших (с небольшим числом ветвей) цепей: метод контурных токов и метод узловых потенциалов. Метод контурных токовМетод контурных токов позволяет уменьшить количество решаемых уравнений в сравнении с системой уравнений по законам Кирхгофа. Данный метод целесообразно применять в тех случаях, когда число независимых контуров цепи меньше числа ее узлов. Количество уравнений по методу контурных токов определяется числом уравнений по второму закону Кирхгофа для рассматриваемой электрической цепи. Метод основывается на том свойстве, что ток в любой ветви может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих по этой ветви. В соответствии с данным методом необходимо выбрать контурные токи таким образом, чтобы каждый из них проходил через один источник тока, а оставшиеся контурные токи выбирать проходящими по ветвям, не содержащим источники тока. Система уравнений по методу контурных токов в виде матрицы будет иметь столько строк и столбцов, столько уравнений необходимо записать по второму закону Кирхгофа для рассматриваемой электрической цепи. Если в электрической цепи имеется источник тока, то добавится столбец в систему уравнений, если два, то два столбца и т.д. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров. Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему линейных уравнений. Рассмотрим расчет на примере цепи, представленной на рис. 1 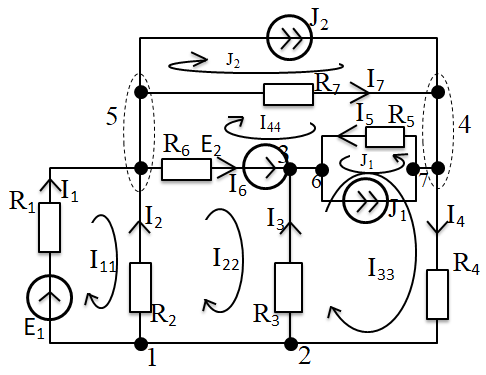 Рис. 1 Для цепи, представленной на рис. 1, найти токи во всех ветвях, если: E1=10 В; Е2=40 В; J1=1 A; J2=2 A; R1=10 Ом; R2=40 Ом; R3=50 Ом; R4=25 Ом; R5=20 Ом; R6=30 Ом; R7=35 Ом. Решение. Рассматриваемая схема замещения состоит из семи узлов (Nу = 7) и шести ветвей (Nв=7), среди них две ветви с источником тока (NJ=2). Направление обхода четырех независимых контуров выбираем по часовой стрелке, а в пятом и шестом контуре ток принимается равным токам источников. В пятом контуре направление берем против часовой стрелки, чтобы J было положительным. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура. Так как у нас четыре контура без источника тока, система будет состоять из четырех уравнений: 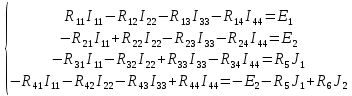 Такую систему уравнений достаточно тяжело решить. Для сокращения числа ветвей и уменьшения числа уравнений выполним преобразование цепи (см. рис. 2).         г) в) б) а) 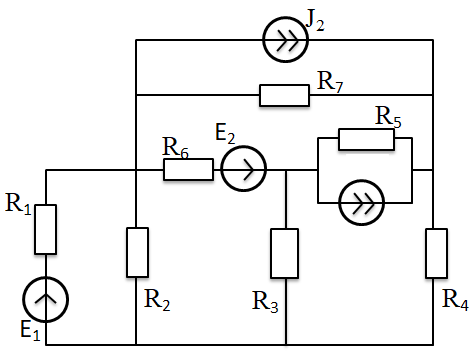  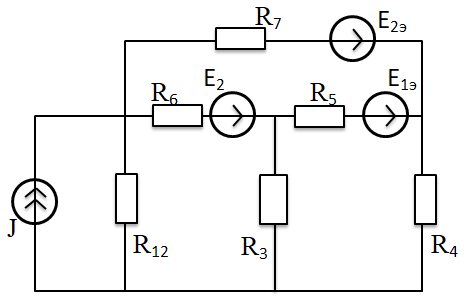  Рис. 2 В схеме идеальные источники тока преобразованы в эквивалентные источники ЭДС. В ней Е1э = J1*R5 = 20 В; Е2э = J2*R7 = 70 В; J=E1/R1=1 А; 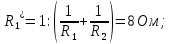 Еэ = J*R12 = 20 В (для удобства переобозначили R12, указанное на схеме на R1*). Еэ = J*R12 = 20 В (для удобства переобозначили R12, указанное на схеме на R1*).И в итоге получаем схему, изображенную на рис. 3 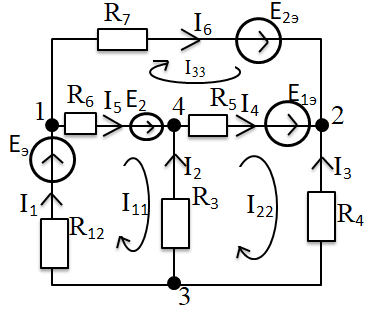 Рис. 3 Новая цепь будет состоять уже из четырех узлов (Nу = 4) и шести ветвей (Nв=6). Направление обхода трех независимых контуров выбираем по часовой стрелке. После всех преобразований можно формировать контурные уравнения: 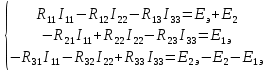 Где R1, R2, R3, R4, R5, R6 - собственные сопротивления контуров, а R11 = R1*+R3+R6 = 88 Ом; R12 = R3 = 50 Ом; R22 = R3+R4+R5 = 95 Ом; R13 = R6 = 30 Ом; R33 = R5+R6+R7 = 85 Ом; R23 = R5 = 20 Ом; - взаимные сопротивления контуров. В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом. 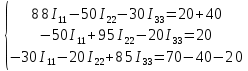 Из данной системы находим контурные токи: 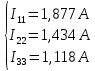 Значение реального тока конкретной ветви составляет алгебраическую сумму контурных токов, протекающих по этой ветви. Определим значения токов: I1 = I11; I1=1,877 А; I2 = I22 - I11; I2=-0,443 А; I3 = I22; I3=1,434 А; I4 = I22 - I33; I4=0,316 А; I5 = I11 - I33; I5=0,759 А; I6 = I33; I6=1,118 А. В случае, где ток получился отрицательным, его направление будет противоположным выбранному направлению тока. Метод узловых потенциаловДанный метод также позволяет уменьшить количество решаемых уравнений в сравнении с системой уравнений по законам Кирхгофа. Данный метод целесообразно применять тогда когда число узлов цепи меньше или равно числу независимых контуров этой цепи. Количество уравнений по методу узловых потенциалов определяется количеством уравнений по первому закону Кирхгофа для рассматриваемой электрической цепи. В соответствии с данным методом, необходимо сначала определить потенциалы всех узлов электрической цепи, а затем с помощью закона Ома определить токи в ветвях. При этом один из узлов электрической схемы, который называют опорным, заземляется, его потенциал становится равен нулю. Узел для заземления выбирается произвольно. Удобно заземлять узел, номер которого имеет наибольшее значение в заданной электрической цепи. Система уравнений по методу узловых потенциалов в виде матрицы будет иметь столько строк и столбцов, столько уравнений необходимо записать по первому закону Кирхгофа для рассматриваемой электрической цепи. Если в электрической цепи имеется ветвь, содержащая только идеальный источник ЭДС. Тогда удобно пронумеровать узлы электрической цепи так, чтобы номер узла с наибольшим значения в заданной электрической цепи, оказался в узле от которого отходит источник ЭДС. Этот узел принимают за опорный и заземляют. Тогда потенциал узла, в который входит источник ЭДС, будет известным и равным величине ЭДС источника. Метод узловых потенциалов использует m=q-1 линейно независимых уравнений по числу независимых узлов. В качестве неизвестных выступают потенциалы узлов, по которым при помощи закона Ома находят токи ветвей. Наличие в цепи идеального источника напряжения упрощает задачу анализа, так как сокращает количество необходимых уравнений, поскольку идеальный источник напряжения определяет (с учетом направления) узловое напряжение узла, к которому он подключен. Алгоритм метода узловых потенциалов состоит из четырех основных этапов: 1. Выбор опорного узла; обозначение направлений узловых напряжений и токов в ветвях. При наличии РИН будем заменять их эквивалентными РИТ. 2. Запись системы линейных уравнений в общем виде; нахождение всех коэффициентов: собственных и взаимных проводимостей и узловых токов. 3. Решение полученной системы и нахождение узловых напряжений. 4. Определение токов в ветвях через узловые напряжения по закону Ома. Рассмотрим данный метод на примере уже преобразованной схемы, представленной на рис. 4 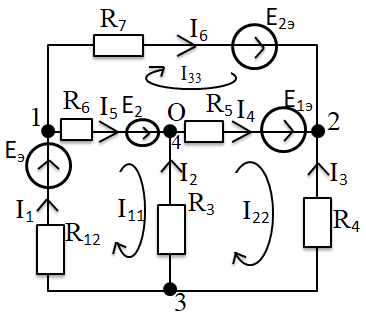 Рис. 4 В качестве опорного выбираем узел О, так как к нему примыкает наибольшее число ветвей. Потенциал у опорного узла принимаем равным нулю. Остальные узловые напряжения направляем к опорному узлу. Система стандартизованных уравнений по первому закону Кхиргофа для этой схемы будет иметь вид: 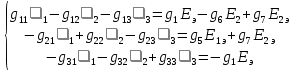 где gn=Rn-1 – проводимость соответствующих сопротивлений (g1=1/R1*; g5=1/R5; g6=1/R6; g7=1/R7). Собственная проводимость узла (суммарная проводимость всех ветвей подходящих к нему): g11=g1+g6+g7=0,187 Ом-1; g22=g4+g5+g7=0,119 Ом-1; g33=g1+g3+g4=0,185 Ом-1; Взаимная проводимость узла (проводимость соединяющих их ветвей): g12=g21=g7=0,028 Ом-1; g13=g31=g1=0,125 Ом-1; g23=g32=g4=0,04 Ом-1; 1, 2, 3 – потенциалы соседних узлов. Подставим данные из первой задачи в систему и решим ее: 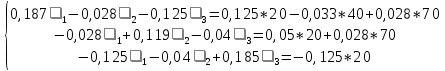 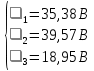 Используем обобщённый закон Ома для нахождения каждого из токов (за i берем потенциал узла из которого ток выходит, а за потенциал узла в который ток входит): Ii = 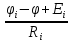 = gi (i-+Ei) = gi (i-+Ei)I1=g1 (3-1+Еэ)=0,446; I2=g3 (3-0)= g23=0,473; I3=g4(3-2) =-0,824; I4=g5(-2+Е1э)=-0,978; I5=g6(1+Е2)=2,51; I6=g7 (1-2-Е2э)=-2,07. В результате значения токов, найденные разными способами, в пределах погрешности совпадают. ЗаключениеСуществует множество различных методов анализа простейших цепей. Метод выбирается от характера самой цепи. В данной курсовой работе были подробно исследованы только два основных метода на примере одной и той же схемы. Так же были выполнены преобразования цепи для ее упрощения и сокращения числа ветвей. В данной схеме на самом деле оказался более простым в решении метод контурных токов, однако независимо от выбора метода анализа цепи, значения токов получаются одинаковыми. . Список использованных источниковНемцов М.В. Электротехника и электроника (6-е изд., стер.) учебник. –М: Академия, 2013. – 480 с. Электротехника и электроника: Учебное пособие для вузов / В.В. Кононенко [и др.]; под ред. В.В. Кононенко. – Изд. 6-е – Ростов н/Д: Феникс, 2010. – 784 с. (Высшее образование). Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.   J2    J2          I7 R7              I5 I44 R5 5 4          R6 E2 J1 3                     I6 I1 7 6 R1        I3 I4 I2 J1              I33 I22 I11 R4              R2 R3 E1     1 2  Рис. 1    E2э R7         R1 E1э E2       R5 R6     Eэ J          R12 J R4 R3 Рис. 1                                    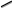 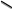 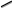                 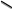 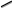        О 4 3 2 1 Eэ I6 I5 R7 R6 E2 I4 I3 I2 I1 E2э R4 R3 I33 I11 I22 R12 R55 E1э |
