физика. V 041 Динамика вращательного движения. Момент силы. Момент импульса. Момент инерции тел кластер П( c041, 7 шт)
 Скачать 455.31 Kb.
|
|
большеймолярной массой и таким же числом молекул, то 1) величина максимума уменьшится 2) площадь под кривой увеличится 3) максимум кривой сместится влево, в сторону меньших скоростей 4) максимум кривой сместится вправо, в сторону больших скоростей :3 S115 – М Распределение Больцмана -5 заданий 1. [Уд1] (ВОМ). Распределение Больцмана характеризует: 1) равновесное распределение частиц по координатам в стационарном потенциальном поле. 2) системы, состоящие как электронейтральных, так и заряженных классических частиц. 3) системы частиц со скоростями близкими к скорости света. :1,2 2. [Уд1] (ВОМ). Формула  описывает распределение одинаковых молекул массой по высоте в изотермической атмосфере; здесь – концентрация молекул при ,n – их концентрация на высоте h. Для этой зависимости справедливы следующие утверждения:1) приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при T2 > T1 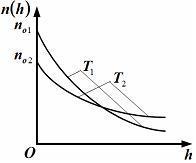 2) приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем m1 > m2 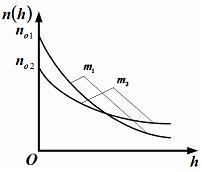 3) приведенные на рисунке кривые соответствуют распределениям для одного и того же газа, причем T2 < T1 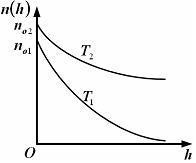 4) приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению m1 < m2 :1,2 3. [Уд1] (ВО1). Отношение концентрации молекул водорода (M1 = 2⋅10-3 кг/моль) к концентрации молекул азота (M2 = 28⋅10-3 кг/моль) равно η0, а на высоте h соответствующее составляет ηh. Если температура Т = 380 Ки ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет  , то высотаh равна … км.1) 3 2) 6 3) 4,5 4) 8,7 :1 4. [Уд1] (ВО1). Отношение концентрации молекул водорода (M1 = 2⋅10-3 кг/моль) к концентрации молекул азота (M2 = 28⋅10-3 кг/моль) равно η0, а на высоте h = 3000 м соответствующее составляет ηh. Если температура Т и ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет , то температура равна … К.1) 380 2) 250 3) 540 4) 410 :1 5. [Уд1] (ВО1). Плотность водорода ρh на высоте h на 10% меньше его плотности ρ0 на уровне моря. Если температура Т = 273 Ки ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, то высота h равна … км. 1) 6,8 2) 9,4 3) 12,2 4) 15,7 :3 C115 – М Распределение Максвелла – 13 заданий 1. [Уд1] (ВО1). Функция распределения Максвелла для молекул газа имеет вид 1)  2) 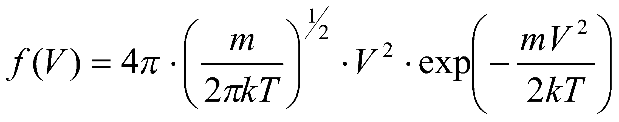 3) 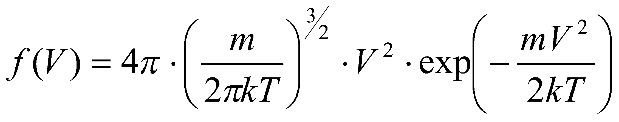 4)  :3 2. [Уд1] (ВО1). Если давление и плотность молекул газа соответственно составляют Р = 40 кПа и ρ = 0,35 кг/м3, то наиболее вероятная скорость равна … м/с. 1) 478 2) 630 3) 250 4) 346 :1 3. [Уд1] (ВО1). Если плотность газа ρ = 0,35 кг/м3, наиболее вероятная скорость его молекул 630 м/с, то давление равно … кПа. 1) 23,4 2) 69,5 3) 47,8 4) 53,6 :2 4. [Уд1] (ВО1). При нагревании некоторого газа средняя арифметическая скорость молекул этого газа увеличилась в 2 раза. При этом наиболее вероятная скорость … раз(а). 1) увеличилась в 2) увеличилась в 4 3) уменьшилась в 8 4) увеличилась в 2 :4 5. [Уд1] (ВО1). В сосуде находятся одинаковые количества азота N2 и водорода H2. Распределение скоростей молекул газа в сосуде будет описываться кривыми, изображенными на рисунке под номером 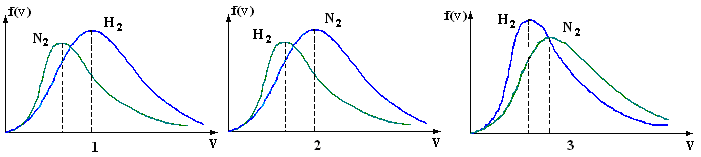 1) 1 2) 2 3) 3 4) правильного рисунка нет :4 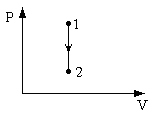 6. [Уд1] (ВО1). На (Р,V) – диаграмме показан процесс, производимый идеальным газом в изолированной сосуде. Начальное и конечное состояния будут соответствовать распределениям скоростей, изображенным на рисунке 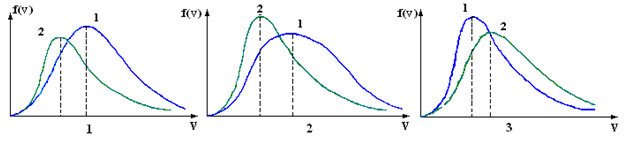 1) 1 2) 2 3) 3 :2 7. [Уд1] (ВО1). В трех одинаковых сосудах находится одинаковое количество газа при разных температурах. Распределение скоростей молекул в сосуде с максимальной температурой будет описывать кривая, обозначенная номером 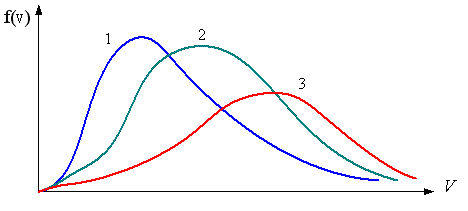 1) 1 2) 2 3) 3 :3 8. [Уд1] (ВО1). Максимальное значение функции распределения Максвелла при данной температуре Т равно  (e - основание натурального логарифма, VB - наиболее вероятная скорость). Если при изменении температуры газа f(VB) уменьшится в 2 раза, то средняя квадратичная скорость молекул газа … раза.1) увеличится в 4 2) уменьшится в 3) уменьшится в 2 4) увеличится в 2 :4 9. [Уд1] (ВОМ). Правильные утверждения, относящиеся к функциям распределения Максвелла и Больцмана: 1) Функция распределения Максвелла позволяет найти распределение молекул по значениям потенциальной энергии. 2) Распределение Больцмана справедливо только в потенциальном поле силы тяжести. 3) Распределение молекул в пространстве устанавливается в результате совместного действия теплового движения и потенциального поля. 4) Распределение Больцмана характеризует распределение частиц классической системы по координатам после установления в системе равновесия. :3,4 10. [Уд1] (ВО1). Если молярные массы азота и кислорода соответственно равны M1= 28⋅10-3 кг/мольи M2= 32⋅10-3 кг/моль, а наиболее вероятные скорости молекул азота и кислорода будут отличаться друг от друга на ΔV = 30 м/c, то температура смеси газов равна … К. 1) 180 2) 256 3) 363 4) 450 :3 11. [Уд1] (ВО1). При некоторой температуре распределение молекул газа по модулям скоростей оказалось таким, что скоростям V1 = 200 м/с и V2 = 800 м/с соответствует одинаковое значение функции распределения Максвелла f(v). Тогда наиболее вероятная скорость молекул этого газа равна … м/с. 1) 250 2) 346 3) 465 4) 630 :3 12. [Уд1] (ВО1). При скорости V1= 800 м/с значения функции распределения Максвелла по модулям скоростей f(V) одинаковы для кислорода и азота (см. рисунок). Молярные массы газов равны, соответственно, M1 = 32⋅10-3 кг/моль и M2 = 28⋅10-3 кг/моль. Тогда смесь газов находится при температуре … К. 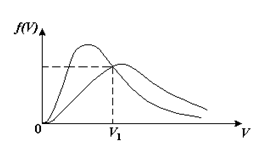 1) 258 2) 471 3) 650 4) 769 :4 13. [Уд1] (ВО1). На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  - доля молекул, скорости которых заключены в интервале от до в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ сменьшеймолярной массой и таким же числом молекул, то 1) высота максимума увеличится 2) площадь под кривой уменьшится 3) максимум кривой сместится вправо, в сторону больших скоростей 4) максимум кривой сместится влево, в сторону меньших скоростей :4 S116 – МУО+КЗ Распределение Больцмана – 4 задания 1. [Уд1] (ВО1). Распределение Больцмана описывает распределение частиц по 1) координатам 2) кинетическим энергиям 3) импульсам 4) скоростям :1 2. [Уд1] (ВОМ). Распределение Больцмана можно использовать, если справедливы утверждения: 1) температура в разных частях системы одинакова 2) температура в разных частях системы неодинакова 3) импульсы всех молекул системы одинаковы 4) система находится в состоянии равновесия :1,4 3. [Уд1] (ВО1). Установленная вертикально закрытая с обоих концов труба наполнена газообразным кислородом M = 32⋅10-3 кг/моль. Высота трубы h = 200 м, ускорение силы тяжести g = 9,8 м/с2. Стенки трубы имеют всюду одинаковую температуру Т = 293 К. Давление газа внутри трубы вблизи ее основания равно Р0 = 105 Па. Давление Рh в трубе вблизи верхнего его конца равно … кПа. 1) 87 2) 110 3) 97 4) 100 :3 4. [Уд1] (ВО1). На взлетной площадке барометр показывает давление P0 = 100 кПа, а в кабине вертолета барометр показывает давление P = 90 кПа. Если температура воздуха (Т = 293 К) и ускорение силы тяжести (g = 9,8 м/с2) не изменяются с высотой и, молярная масса воздуха равна M = 29⋅10-3 кг/моль, то высота h, на которойлетит вертолет, равна … м. 1) 800 2) 900 3) 1000 4) 750 :2 C116 – МУО+КЗ Распределение Максвелла – 4 задания 1. [Уд1] (ВОМ) Абсолютное число dN молекул идеального газа, скорости которых при данной температуре T заключены в интервале от V до V + dV, зависит от: 1) температуры газа 2) от общего числа N молекул этого газа 3) от объема, занимаемого газом 4) от значения скорости V, в окрестности которой выбран рассматриваемый интервал dV :1,2,4 2. [Уд1] (ВО1). Функция распределения Максвелла 1) не имеет экстремальный вид 2) является величиной безразмерной 3) может быть величиной отрицательной 4) при заданной температуре может соответствовать двум различным скоростям молекул газа :4 3. [Уд1] (ВОМ). В статистике Максвелла функция распределения имеет вид  . Верные утверждения:1) f(V) - относительное число молекул, скорости которых лежат в единичном интервале скоростей вблизи заданного значения скорости V. 2) f(V)dV - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. 3) f(V)NdV - число молекул, скорости которых заключены в интервале скоростей от V до V+dV. 4) 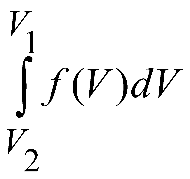 - абсолютное число молекул, скорости которых заключены в интервале от скоростиV1 до скорости V2.:1,2,3 4. [Уд1] (ВОМ). На рисунке изображен график функции распределения Максвелла молекул идеального газа по модулю скоростей. Тогда площадь заштрихованной полоски есть: 1) относительное число молекул  , скорости которых заключены в интервале отV до V + dV.2) вероятность того, что скорость данной молекулы имеет значение, заключенное в интервале от V до V + dV. 3) доля молекул, скорости которых заключены в интервале от V до V + dV. 4) число частиц, скорости которых заключены в интервале от V до V + dV. :1,2,3 Дисциплина: Физика Тема: 120 Термодинамика V124 – П Энтропия и второе начало термодинамики. S124 –П Энтропия и второе начало термодинамики (10 заданий) . 1. [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы уменьшается в процессах: 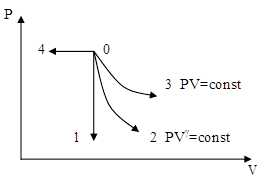 1) 0 → 1 2) 0 → 2 3) 0 → 3 4) 0 → 4 :1, 4 2. [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы возрастает в процессах: 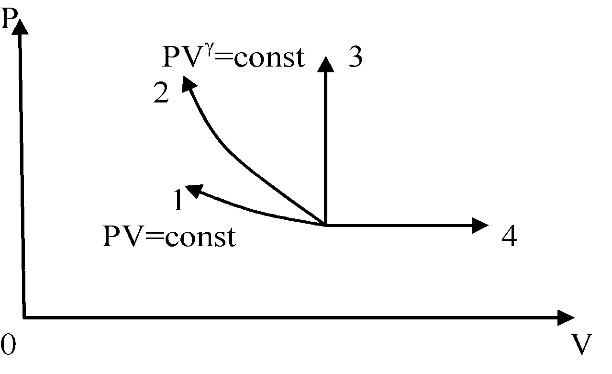 1) 0 → 1 2) 0 → 2 3) 0 → 3 4) 0 → 4 :3, 4 3. [Уд1] (ВОМ). Один моль гелия и один моль азота, находящиеся в закрытых сосудах, нагрели от температуры Т1 до температуры Т2. Тогда 1) изменения энтропий этих газов не зависят от объемов сосудов 2) изменения энтропий этих газов не зависят от скорости нагрева 3) ΔSN2 =ΔSHe 4) ΔSN2 >ΔSHe :2, 4 4. [Уд1] (ВО1). Изотермическое расширение одного моля азота проведено до удвоения объема. Такое же увеличение объема осуществлено для моля гелия. Тогда 1) ΔSN2 >ΔSHe 2) ΔSN2 <ΔSHe 3).Δ SN2 =Δ SHe 4) изменения энтропий этих газов зависят от скорости нагрева :3 5. [Уд1] (ВОМ). Правильные утверждения: 1) равновесие термодинамическое состояние – это такое состояние термодинамической системы, при котором все ее термодинамические параметры остаются постоянными сколь угодно долго. 2) термодинамический процесс – это любое изменение термодинамического состояния системы. 3) неравновесный процесс – процесс, состоящий из ряда следующих друг за другом равновесных состояний. 4) обратимый процесс всегда является равновесным процессом. : 1, 2, 4 6. [Уд1] (ВО1). Воду массой m = 0,1 кг нагревают от 0°С до 100°С и превращают в пар. Удельная теплоемкость воды cУД = 4,19⋅103 Дж/кг⋅К. Изменение энтропии при нагревании равно … Дж/К. 1) 131 2) 250 3) 347 4) 589 :1 7. [Уд1] (ВО1). При изобарическом расширении массы m = 8 г гелия от объема V1 = 10 л до объема V2 = 25 л приращение ΔS энтропии равно … Дж/К. 1) 14,9 2) 38,1 3) 37,6 4) 43,5 :2 8. [Уд1] (ВО1). При изотермическом расширении массы m = 6 г водорода от давления p1 = 100 кПа до давления p2 = 50 кПа приращение ΔS энтропии равно … Дж/К. 1) 17,3 2) 52,8 3) 87,6 4) 46,5 :1 9. [Уд1] (ВО1). Масса |