Теория по погрешностям. В физическом практикуме

• Название: В физическом практикуме
• Анкор: Теория по погрешностям
• Дата: 27.05.2021
• Размер: 105 Kb.
• Имя файла: Теория по погрешностям.doc
• Тип: Практикум; #210556

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

В ФИЗИЧЕСКОМ ПРАКТИКУМЕ
Измерения и погрешности измерений
Физика -  наука экспериментальная, это означает, что физические законы устанавливаются и проверяются путем накопления и сопоставления экспериментальных данных. Цель физического практикума заключается в том, чтобы студенты изучили на опыте основные физические явления, научились правильно измерять числовые значения физических величин и сопоставлять их с теоретическими формулами.

Все измерения можно разделить на два вида – прямые и косвенные.

При прямых измерениях значение искомой величины непосредственно получается по показаниям измерительного прибора. Так, например, длина измеряется линейкой, время по часам и т. д.

Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными.

Измерение любой величины не дает абсолютно точного значения этой величины. Каждое измерение всегда содержит некоторую погрешность (ошибку). Ошибкой называют разность между измеренным и истинным значением.

Ошибки принято делить на систематические и случайные.

Систематической называют ошибку, которая остается постоянной на протяжении всей серии измерений. Такие погрешности обусловлены несовершенством измерительного инструмента (например, смещением нуля прибора) или методом измерений и могут быть, в принципе, исключены из конечного результата введением соответствующей поправки.

К систематическим ошибкам относятся также погрешность измерительных приборов. Точность любого прибора ограничена и характеризуется его классом точности, который, как правило, обозначен на измерительной шкале.

Случайной называется ошибка, которая изменяется в разных опытах и может быть и положительной и отрицательной. Случайные ошибки обусловлены причинами, зависящими как от измерительного устройства, (трение, зазоры, и т. п..), так и от внешних условий (вибрации, колебания напряжения в сети и т.п.).

Случайные ошибки нельзя исключить опытным путем, но их влияние на результат можно уменьшить многократными измерениями.

ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ

СРЕДНЕЕ ЗНАЧЕНИЕ И СРЕДНЯЯ АБСОЛЮТНАЯ ОШИБКА.
Предположим, что мы проводим серию измерений величины Х. Из-за наличия случайных ошибок, получаем n различных значений:

Х₁, Х₂, Х₃… Х_n

В качестве результата измерений обычно принимают среднее значение

(1)

Разность между средним значением и результатом i – го измерения назовем абсолютной ошибкой этого измерения




В качестве меры ошибки среднего значения можно принять среднее значение абсолютной ошибки отдельного измерения

(2)

Величина называется средней арифметической (или средней абсолютной) ошибкой.

Тогда результат измерений следует записать в виде

(3)

Для характеристики точности измерений служит относительная ошибка, которую принято выражать в процентах

(4)
СРЕДНЯЯ КВАДРАТИЧНАЯ ОШИБКА.
При ответственных измерениях, когда необходимо знать надежность полученных результатов, используется средняя квадратичная ошибка  (или стандартное отклонение), которая определяется формулой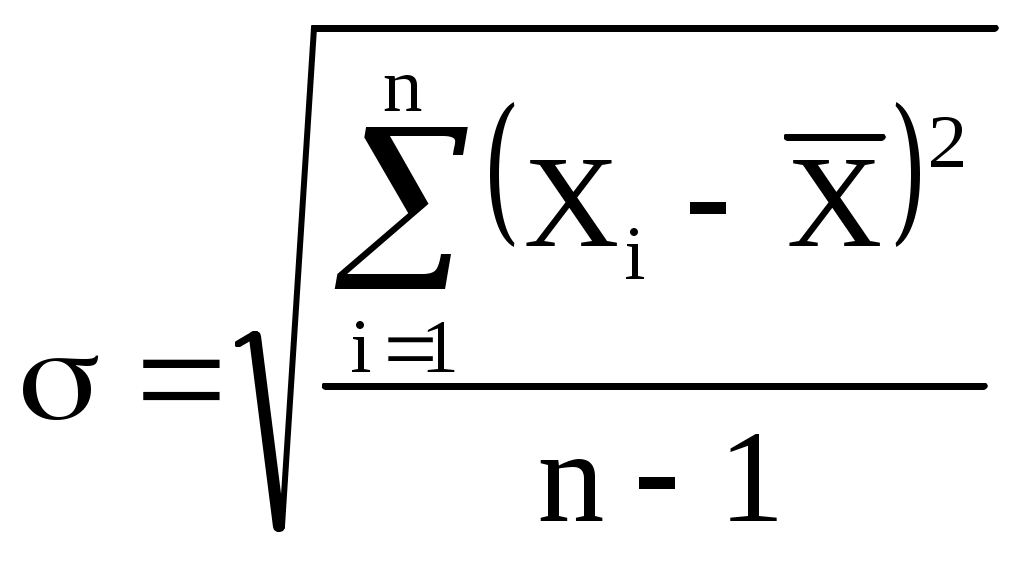

(5)

Величина  характеризует отклонение отдельного единичного измерения от истинного значения.

Если мы вычислили по n измерениям среднее значение 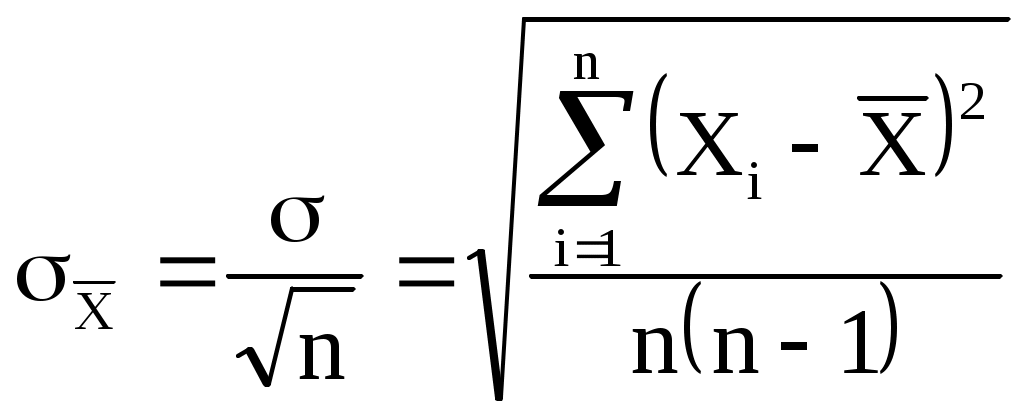по формуле (2), то это значение будет более точным, то есть будет меньше отличаться от истинного, чем каждое отдельное измерение. Средняя квадратичная ошибка среднего значения равна

(6)

где  - среднеквадратичная ошибка каждого отдельного измерения, n – число измерений.

Таким образом, увеличивая число опытов, можно уменьшить случайную ошибку в величине среднего значения.

В настоящее время результаты научных и технических измерений принято представлять в виде

(7)

Как показывает теория, при такой записи мы знаем надежность полученного результата, а именно, что истинная величина Х с вероятностью 68% отличается от не более, чем на .

При использовании же средней арифметической (абсолютной) ошибки (формула 2) о надежности результата ничего сказать нельзя. Некоторое представление о точности проведенных измерений в этом случае дает относительная ошибка (формула 4).

При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).

Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки среднего (формулы 5 и 6).
УЧЕТ СИСТЕМАТИЧЕСКИХ ОШИБОК.
Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.

Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм; для измерений штангенциркулем –

0,1 – 0,05 мм; микрометром – 0,01 мм.

Часто в качестве систематической ошибки берется половина цены деления прибора.

На шкалах электроизмерительных приборов указывается класс точности. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆Х по формуле



где К – класс точности прибора, Х_пр – предельное значение величины, которое может быть измерено по шкале прибора.

Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более



Среднее значение полной погрешности складывается из случайной и систематической погрешностей.



Ответ с учетом систематических и случайных ошибок записывается в виде



ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
В физических экспериментах чаще бывает так, что искомая физическая величина сама на опыте измерена быть не может, а является функцией других величин, измеряемых непосредственно. Например, чтобы определить объём цилиндра, надо измерить диаметр D и высоту h, а затем вычислить объем по формуле



Величины D и h будут измерены с некоторой ошибкой. Следовательно, вычисленная величина V получится также с некоторой ошибкой. Надо уметь выражать погрешность вычисленной величины через погрешности измеренных величин.

Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку.

Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.

Пусть искомая величина φ является функцией нескольких переменных Х, У, Z…

φ(Х, У, Z…).

Путем прямых измерений мы можем найти величины , а также оценить их средние абсолютные ошибки … или средние квадратичные ошибки _Х, _У, _Z…

Тогда средняя арифметическая погрешность  вычисляется по формуле



где  - частные производные от φ по Х, У, Z. Они вычисляются для средних значений …

Средняя квадратичная погрешность вычисляется по формуле



Пример. Выведем формулы погрешности для вычисления объёма цилиндра.

а) Средняя арифметическая погрешность.

Величины D и h измеряются соответственно с ошибкой D и h.

Погрешность величины объёма будет равна



б) Средняя квадратичная погрешность.

Величины D и h измеряются соответственно с ошибкой _D, _h.

Погрешность величины объёма будет равна



Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять относительную погрешность. Для этого (в случае средней арифметической погрешности) надо проделать следующее.

1. Прологарифмировать выражение.

2. Продифференцировать его.

3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.

4. Взять выражение перед различными дифференциалами по модулю.

5. Заменить значки дифференциалов d на значки абсолютной погрешности .

В итоге получится формула для относительной погрешности



Затем, зная , можно вычислить абсолютную погрешность 

 = 

Пример.









Аналогично можно записать относительную среднюю квадратичную погрешность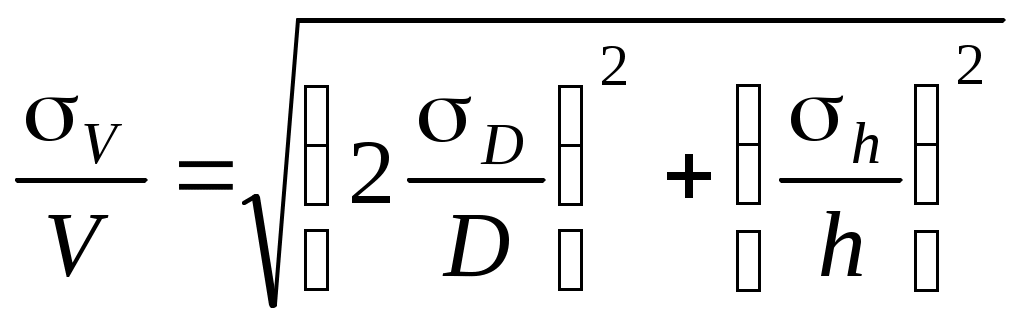


Правила представления результатов измерения следующие:

1. 
   погрешность должна округляться до одной значащей цифры:
   

правильно  = 0,04,

неправильно -  = 0,0382;

2. 
   последняя значащая цифра результата должна быть того же порядка величины, что и погрешность:
   

правильно  = 9,830,03,

неправильно -  = 9,8260,03;

3. 
   если результат имеет очень большую или очень малую величину, необходимо использовать показательную форму записи - одну и ту же для результата и его погрешности, причем запятая десятичной дроби должна следовать за первой значащей цифрой результата:
   

правильно -  = (5,270,03)10^-5,

неправильно -  = 0,00005270,0000003,

 = 5,2710^-50,0000003,

 = = 0,0000527310^-7,

 = (5273)10^-7,

 = (0,5270,003) 10^-4.

4. 
   Если результат имеет размерность, ее необходимо указать:
   

правильно – g=(9,820,02) м/c²,

неправильно – g=(9,820,02).
Правила построения графиков
1. Графики строятся на миллиметровой бумаге.

2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х), значения функции - на оси ординат (ось у).

3. Из экспериментальных данных определить пределы изменения аргумента и функции.

4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин.

5. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой).

6. Провести через экспериментальные точки плавную кривую (прямую) так, чтобы эти точки приблизительно в равном количестве располагались по обе стороны от кривой.