В. М. Деревяшкин и. Б. Елистратова основы научных исследований
 Скачать 3.1 Mb. Скачать 3.1 Mb.
|
|
Общие сведения об экспериментальных исследованиях Эксперимент – это важнейшая составная часть научных исследований. Его основой является научно поставленный опыт с точно учитываемыми и управляемыми условиями. Основной целью эксперимента являются выявление свойств исследуемых объектов, проверка справедливости гипотез и на этой основе широкое и глубокое изучение темы научного исследования. Они различаются [3,20]: по способу формирования условий (естественный и искусственный); по целям исследования (преобразующие, констатирующие, контролирующие, поисковые, решающие); по организации проведения (лабораторные, натурные и т.д.); по структуре изучаемых объектов и явлений (простые, сложные) и т.д. Естественный эксперимент предполагает проведение опытов в естественных условиях существования объекта исследования. Искусственный эксперимент предполагает формирование искусственных условий. Преобразующий эксперимент включает активное изменение структуры и функций объекта исследования в соответствии с выдвинутой гипотезой, формирование новых связей и отношений между компонентами объекта или между исследуемым объектом и другими объектами. Исследователь преднамеренно создает условия, которые должны способствовать формированию новых свойств и качеств объекта. Констатирующий эксперимент используется для проверки определенных предположений. Контролирующий эксперимент сводится к контролю за результатами внешних воздействий над объектом исследования с учетом его состояния, характера воздействия и ожидаемого эффекта. Поисковый эксперимент проводится в том случае, если затруднена классификация факторов, влияющих на изучаемое явление вследствие отсутствия достаточных предварительных данных. По результатам поискового эксперимента устанавливаются значимость факторов, осуществляется отсеивание незначимых. Решающий эксперимент ставится для проверки справедливости основных положений фундаментальных теорий в том случае, когда две или несколько гипотез одинаково согласуются со многими явлениями. Это согласие приводит к затруднению, какую именно из гипотез считать правильной. Решающий эксперимент дает такие факты, которые согласуются с одной из гипотез и противоречат другой. Лабораторный эксперимент проводится в лабораторных условиях с применением типовых приборов, специальных моделирующих установок, стендов и т.д. Чаще всего в лабораторном эксперименте изучается не сам объект, а его образец (модель). Натурный эксперимент проводится в естественных условиях и на реальных объектах. В зависимости от места проведения испытаний он делится на производственный, полевой, полигонный и т.д. Простой эксперимент используется для изучения объектов, не имеющих разветвленной структуры, с небольшим количеством взаимосвязанных и взаимодействующих элементов, выполняющих простейшие функции. Сложный эксперимент изучает явления или объекты с разветвленной структурой и большим количеством взаимосвязанных и взаимодействующих элементов, выполняющих сложные функции. Особое значение имеет правильная разработка методики эксперимента. Методика – это совокупность мыслительных и физических операций, размещенных в определенной последовательности, в соответствии с которой достигается цель исследования. При разработке методики проведения эксперимента необходимо предусматривать: проведение предварительного целенаправленного наблюдения над изучаемым объектом или явлением с целью определения исходных данных (гипотез, выбора варьирующих факторов); создание условий, в которых возможно экспериментирование (подбор объектов для экспериментального воздействия, устранение влияния случайных факторов); определение пределов измерений; систематическое наблюдение за ходом развития изучаемого явления и точные описания фактов; проведение систематической регистрации измерений и оценок фактов различными средствами и способами; создание повторяющихся ситуаций, перекрестных воздействий, изменение их характера и условий; создание усложненных ситуаций с целью подтверждения или опровержения ранее полученных данных; переход от эмпирического изучения к логическим обобщениям, к анализу и теоретической обработке полученного фактического материала. Перед каждым экспериментом составляется его план, который включает [3]: цель и задачи эксперимента; выбор варьируемых факторов; обоснование объема эксперимента, числа опытов; порядок реализации опытов; определение последовательности изменения факторов; выбор шага изменения факторов, задание интервалов между будущими экспериментальными точками; обоснование средств измерений; описание проведения эксперимента; обоснование способов обработки и анализа результатов эксперимента. Рассмотрим представленный план более подробно. Важным этапом подготовки эксперимента является определение его целей и задач. Количество задач не должно быть слишком большим (лучше 3-4, максимально 8-10) [20]. Перед экспериментом надо выбрать варьируемые факторы, т.е. установить основные и второстепенные характеристики, влияющие на исследуемый процесс, проанализировать расчетные схемы процесса. Правильный выбор основных и второстепенных факторов играет важную роль в эффективности эксперимента, поскольку он сводится к нахождению зависимостей между этими факторами. Необходимо также обосновать набор средств измерений, оборудования, машин и аппаратов. Поэтому важно быть хорошо знакомым с выпускаемой в стране измерительной аппаратурой. Нередко возникает потребность в создании уникальных приборов, установок, стендов для выполнения эксперимента. При этом их разработка и конструирование должны быть тщательно обоснованы теоретическими расчетами. Одним из самых ответственных моментов в эксперименте является установление точности измерений и погрешности. Методы измерений должны базироваться на законах специальной науки – метрологии, изучающей средства и методы измерений. При экспериментальном исследовании одного и того же процесса повторные отсчеты на приборах, как правило, неодинаковы. Отклонения возможны по ряду причин: несовершенство приборов, неоднородность свойств изучаемого материала и др. Поэтому эксперимент никогда не обходится одним измерением, а следовательно, нужно знать их минимальное количество, которое смогло бы обеспечить устойчивое среднее значение измеряемой величины, удовлетворяющей заданной степени точности. В методике эксперимента подробно разрабатывается процесс его проведения; составляется последовательность операций измерений и наблюдений; детально описывается каждая операция в отдельности с учетом выбранных средств для проведения эксперимента; обосновываются методы контроля качества операций, обеспечивающие при минимальном количестве измерений высокую надежность и заданную точность; разрабатываются формы журналов для записи результатов наблюдений и измерений. Важным разделом методики является выбор методов обработки и анализа экспериментальных данных. Обычно результаты экспериментов сводятся в следующие формы записи: таблицы, графики, формулы, что позволяет быстро анализировать полученную информацию. Особое внимание в методике должно быть уделено математическим методам обработки и анализу опытных данных, например, установлению эмпирических зависимостей, аппроксимации связей между варьирующими характеристиками, установлению критериев и доверительных интервалов и др. На объем и трудоемкость проведения экспериментальных работ существенно влияет вид эксперимента. Например, натурные и полевые эксперименты, как правило, имеют большую трудоемкость, что следует учитывать при планировании. После установления объема экспериментальных работ составляется перечень необходимых средств измерений, объем материалов, список исполнителей, календарный план и смета расходов. Программу эксперимента рассматривает научный руководитель, обсуждают в научном коллективе (например, на заседании кафедры или научно-технического совета) и утверждают в установленном порядке. Метрология в экспериментальных исследованиях Важное место в экспериментальных исследованиях занимают измерения. Измерение – это нахождение значения физической величины опытным путем с помощью специальных технических средств. Суть измерения составляет сравнение измеряемой величины с известной величиной, принятой за единицу (эталон) [21]. Теорией и практикой измерений занимается метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. К основным проблемам метрологии относятся [3]: общая теория измерений; единицы физических величин и их системы; методы и средства измерений; методы определения точности измерений; основы обеспечения единства измерений. Важнейшее значение в метрологии отводятся эталонам и образцовым средствам измерений. К эталонам относятся средства измерений, обеспечивающих воспроизведение и хранение единицы с целью передачи ее размера нижестоящим средствам измерения. Эталоны выполнены по особой спецификации. Эталонная база России содержит более 120 государственных эталонов, в том числе, например: единицы длины, массы и др. Образцовые средства измерений служат для проверки по ним рабочих средств измерения, постоянно используемых непосредственно в исследованиях. Различают несколько основных методов измерения [21]. Метод непосредственной оценки – определение значения величины непосредственно по отсчетному устройству измерительного прибора прямого действия (например, измерение массы на циферблатных весах). Метод сравнения с мерой – измеряемая величина сравнивается с величиной, воспроизводимой мерой (например, измерение массы на рычажных весах с уравновешиванием гирями). Дифференциальный метод – на измерительный прибор воздействует разность измеряемой и известной величины, воспроизводимой мерой (например, измерения, выполняемые при проверке мер длины сравнением с образцовой мерой на компараторах). Нулевой метод – результирующий эффект воздействия величины на прибор доводят до нуля (например, измерение электрического сопротивления мостом с полным его уравновешиванием). Метод замещения – измеренную величину замещают известной величиной, воспроизводимой мерой (например, взвешивание с поочередным помещением измеряемой массы и гири на одну и ту же чашку весов). Метод совпадений – разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряется с использованием совпадения отметок шкал или периодических сигналов. Неотъемлемой частью экспериментальных исследований являются средства измерения – совокупность технических средств, имеющих нормированные погрешности, которые дают необходимую информацию для экспериментатора. В настоящее время в России выпускается большое количество средств измерений и наблюдений для измерения показателей физических, механических, химических свойств, а также структуры материала и изделия и т.д. К средствам измерений относят меры, измерительные приборы, установки и системы. Одна из важнейших характеристик средства измерения является погрешность. Она возникает вследствие недоброкачественных материалов, комплектующих изделий, применяемых для изготовления приборов; плохого качества изготовления приборов; неудовлетворительной эксплуатации и др. Рассмотрим основные характеристики прибора. Чувствительность – способность отсчитывающего устройства реагировать на изменения измеряемой величины. Точность – характеристика, связанная с суммарной погрешностью. Стабильность – свойство отсчетного устройства обеспечивать постоянство показаний одной и той же величины. Любое средство измерения должно подвергаться поверке на точность. Рабочая поверка проводится в низовых звеньях организации каждым экспериментатором непосредственно перед началом измерений и наблюдений. Государственная поверка за обеспечением в стране единства мер проводится государственными метрологическими институтами и лабораториями по надзору за стандартами и измерительной техникой. Ведомственная поверка осуществляется в периоды между государственными по специальному графику, разработанному для данной организации. Она мало чем отличается от государственных поверок, но, как правило, проводится по сокращенной программе. Организация рабочего места экспериментатора Рабочее место – часть рабочего пространства, на которое распространяется непосредственное воздействие экспериментатора в процессе исследования. Рабочее пространство – часть лабораторного или производственного помещения, оснащенная необходимыми экспериментальными средствами и обслуживаемая одним или группой исследователей. Рабочее пространство может быть [3]: стационарным (в лабораториях, научно-исследовательских учреждениях, полигонах); условно-стационарным (в передвижных лабораториях, временных полигонах); мобильным (в ходовых лабораториях). Лаборатория представляет собой специально оборудованное помещение, в котором производятся экспериментальные исследования. В соответствии с особенностями рабочего пространства можно выделять два типа исследовательских лабораторий: стационарные и передвижные. Рабочее место стационарной лаборатории комплектуется специальным рабочим столом. В зависимости от назначения лаборатории каждый лабораторный стол может обеспечиваться водой, электричеством, газом, паром, сжатым воздухом и общим вакуумом. На столах размещаются также штепселя для включения электроприборов, настольных ламп, вычислительных машинок, нагревательных приборов (паяльники, плитки), размещаемых на кусках толстого листового асбеста. Особое внимание следует уделять освещенности рабочего места. Оборудование передвижных лабораторий близко к стационарным, но несколько уступает им из-за нехватки площадей. Передвижные лаборатории вместо лабораторных столов оснащаются откидными столиками для ведения необходимых записей в процессе проведения эксперимента. Все анализы, определения и наблюдения необходимо записывать в специальный журнал, даже если результаты одного статистического ряда резко отличаются от соседних измерений. В дальнейшем это позволит установить причины отклонений. Кроме того, в журнал вносятся простейшие расчеты, необходимые в течение эксперимента. При проведении эксперимента необходимо непрерывно следить за средствами измерений, правильностью их показаний, периодически проводить их поверку, не допускать посторонних лиц в рабочую зону. Следует также не забывать о технике безопасности во время проведения эксперимента. Особое место при проведении экспериментальных исследований принадлежит анализу результатов эксперимента. Это завершающая часть, на основе которой делают вывод о подтверждении гипотезы научного исследования. Предварительную обработку результатов эксперимента и их анализ необходимо проводить перед каждым последующим измерением, что позволит контролировать исследуемый процесс, корректировать эксперимент и повышать его эффективность. Результаты экспериментов оформляются протоколом, который подписывается экспериментатором и, если эксперимент был производственным, руководителем производства. Влияние различных факторов на ход и качество эксперимента В процессе проведения эксперимента измерения различных показателей не могут быть выполнены абсолютно точно, поскольку сами измерительные приборы имеют определенную погрешность, которая помимо указанных выше причин, может возникать вследствие недостаточно тщательного проведения опыта, влияния различных неучтенных факторов в процессе опыта, субъективных особенностей экспериментатора. В качестве примера можно привести следующие факторы. Систематические погрешности – при повторных экспериментах остаются постоянными (или изменяются по известному закону). Они могут быть постоянными или переменными, увеличивающимися или уменьшающимися в процессе эксперимента. Их обязательно нужно исключать путем регулировки или ремонта средств измерения, тщательной проверки их установки, устранения нежелательных воздействий внешней среды. Случайные погрешности – возникают случайно при повторном измерении. Их разновидность – грубые погрешности или промахи, существенно превышающие систематические или случайные погрешности. В большинстве случаев они вызваны ошибками экспериментатора. Субъективная погрешность – вызвана психологическими (психологические барьеры и инерционность мышления) или психофизическими причинами (дефект зрения экспериментатора). Иногда исследователь в процессе анализа результатов эксперимента бессознательно подгоняет экспериментальные данные для подтверждения ранее выдвинутой гипотезы. Иногда ошибки эксперимента связаны с тем, что исследователь не представляет себе четко, что он собирается получить. В результате могут быть не учтены важнейшие факторы, что существенно затруднит анализ экспериментальных данных. Все вышеизложенное показывает, что любой результат эксперимента должен восприниматься критически и многократно проверяться. Перепроверку результатов эксперимента целесообразнее осуществлять в другое время дня или, если есть возможность, по истечении нескольких дней. После завершения всех серий эксперимента исследователь принимает то или иное решение [3]: признать основную часть работы законченной; провести дополнительный сбор информации и отбор материала с целью подтверждения гипотезы; признать работу неудавшейся и т.д. Если самостоятельные опыты продолжаются длительное время, рекомендуется периодически проводить их обсуждение в научном коллективе. Это позволяет своевременно скорректировать ход эксперимента и направить его в требуемое русло. Задания для самоконтроля Чтоозначает слово “метод”? В чем заключается цель теоретических исследований? Что относится к основным задачам и этапам теоретического исследования. Что лежит в основе создания модели? Какие стадии включаются в процесс проведения теоретических исследований? Какие стадии включаются в процесс с математической формализации задачи? Что относится к понятию «случайные события»? Что относится к основным методам измерения? В чем основное отличие рабочего места от рабочего пространства? Чем обоснована необходимость перепроверка результатов измерений? МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ Графическое представление экспериментальных данных Графическое представление экспериментальных данных — наиболее наглядное (например, по сравнению с табличным или аналитическим), позволяет выявить общий характер функциональной зависимо- сти изучаемых физических величин, сравнительно легко установить наличие экстремумов функции, пределов увеличения (уменьшения) функций. Обычно при графическом представлении применяют прямоугольную систему координат. На плоскость наносят точки, отображающие экспериментальные данные. Если попытаться провести линию через все точки (соединить точки отрезками прямых), то она будет иметь резкие искривления (это будет ломаная линия) (рис. 6.1). 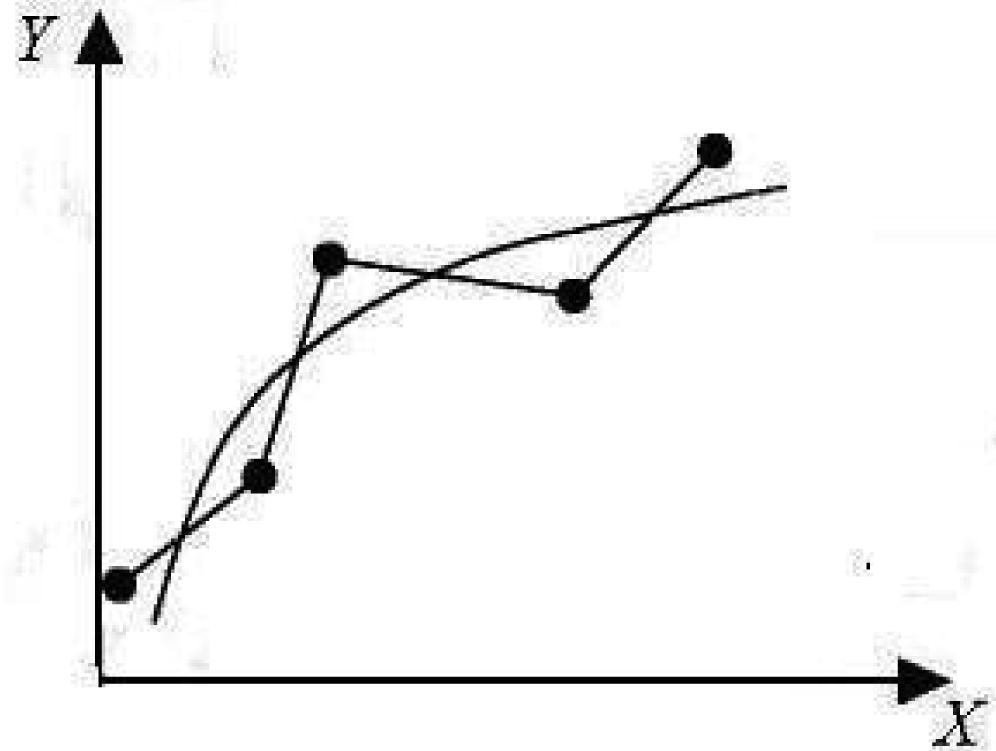 Рисунок 6.1-Графическое представление функции В естественных процессах такие искривления (на математическом языке — быстрые изменения первой производной) встречаются редко. Поскольку в экспериментальных данных всегда присутствуют ошибки измерения, график, проведенный через все экспериментальные точки, фактически отражает воздействие случайных мешающих факторов на результат измерения, а не исследуемоефизическоеявление. Поэтому при построении графика стараются провести плавную линию, как можно ближе проходящую ко всем экспериментальным точкам. Иногда при построении графика выясняется, что некоторые точки резко удалены от кривой. В этих случаях, если нет оснований предполагать наличие скачка функции, резкое отклонение, скорее всего, объясняется грубой ошибкой измерения или промахом. Эксперимент следует повторить в диапазоне резкого отклонения данных. Графики функций, имеющие сложный немонотонный вид (например, имеющие экстремумы), требуют тщательного вычерчивания в зонах изгибов и перегибов.На этих участках шаг изменения независимой переменой в эксперименте должен быть значительно меньше, чем на плавных участках. Часто при проведении экспериментальных измерений приходится иметь дело с функцией двух переменных z= f(x, y). В этом случае одну из переменных, например у, при построении используют в качестве параметра. В результате график (рис. 6.2) представляет собой семейство кривых z=f(x) при у=у1, у=у2, … у=уn. 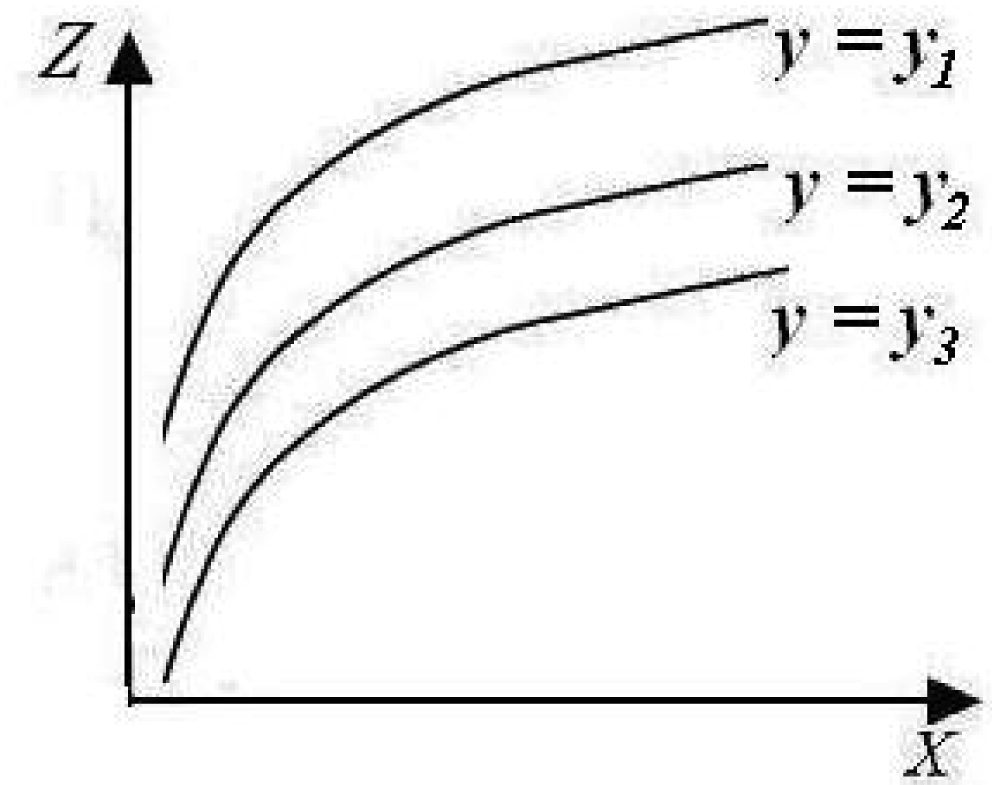 Рисунок 6.2 - Семейство кривых z=f(x) Еще одна проблема при построении графика — рациональный выбор масштаба. Для увеличения точности построения необходимо, чтобы график заполнял всю площадь листа. Поэтому следует определить диапазон изменений переменных по координатным осям и соответствующим образом выбрать шкалы осей (не обязательно вести отсчет от нуля!).Масштаб осей, таким образом, получится автоматически. Приведенные рекомендации могут оказаться недостаточными, если одна или обе переменные имеют большой диапазон изменений, например, несколько порядков. В этом случае применяют полулогарифмический у=f(lgx) или логарифмический lgy= f(lgx) масштабы. 6.2 Аппроксимация экспериментальных данных Термин аппроксимация (от латинского approximo)означает замену одних математических объектов другими, более простыми и в том или ином смысле близкими к исходным. Задача аппроксимацииможет возникнуть, например при обработке экспериментальных данных, когда в результате некоторых измерений получена связь независимой переменной х и зависимой пере- меной. Задача аппроксимации возникает также и в случае, когда для относительно сложной функции требуется получить более простое выражение, которое легко интегрируется или анализируется тем или иным стандартным методом. Например, разложение функции в ряд Тейлора и использова / // ние в качестве аппроксимирующей функции только нескольких первых членов этого ряда позволяет существенно упростить исходную функцию для дальнейшего анализа. Очевидно, что качество аппроксимации может быть оценено двумя показателями: 1 — точность аппроксимации; 2 — простота аппроксимирующей функции. Причем данные показатели противоречивы. Процедура аппроксимации включает в себя два этапа: выбор типа аппроксимирующей функции (это может быть многочлен степени п,в частности, при п= 1 и п= 2 — соответственно прямая и парабола, экспонента, синусоида, гипербола, логарифмическая функция и другие функции); выбор параметров аппроксимирующей функции (коэффициентов многочлена, показателя экспоненты, амплитуды, часто- ты и фазы синусоиды и т. д.), обеспечивающих наилучшее приближение аппроксимирующей функции к исходным данным. При этом обязательно должен быть заранее сформулирован критерий оценки качества приближения. Если исходная экспериментальная или расчетная зависимость задана в виде набора точек (хiyi), i= 1, 2, ..., k, где k — количество точек, то при аппроксимации возникает естественное желание наиболее полно использовать имеющуюся информацию: т. е. подобрать такую функцию, значения которой во всех точках хiсовпадают со значениями yi. Эта задача была решена во второй половине XVIII века французским математиком Лагранжем, который предложил так называемый «интерполяционный многочлен п-го порядка» в виде суммы (п+1) слагаемых. Интерполяционный многочлен — частный случай аппроксимирующей функции — позволяет вычислить значение f(x) = Pn(x) для любого х, причем в узлах интерполяции — точках (хiyi) —выполняется условие Pn(xi) =yi; i= 1, ..., n+1. Интерполяционный многочлен n-го порядка проходит через k= п +1 исходных точек. Если точек достаточно много, то и многочлен будет иметь высокую степень, т. е. аппроксимирующая функция получится сложной. Кроме того, стремление провести аппроксимирующую функцию через исходные точки, особенно при их экспериментальном происхождении, не разумно из-за наличия ошибок измерения. Поэтому следует ограничиться невысокой степенью многочлена п = 1, 2 и 3 так, чтобы график аппроксимирующей функции, соответственно прямая, парабола или кубическая парабола, адекватно отражал общий ход экспериментальной зависимости. При таком подходе количество определяемых параметров аппроксимирующей функции меньше количества точек k, используемых для этого. Поэтому необходимо выбрать специальные критерии качества аппроксимирующей функции. На практике чаще других используются следующие два критерия: Критерий равномерного приближения. Критерий наименьших квадратов. |
