лабораторная работа 6-1. лр 6-1. В последовательном колебательном контуре

• Название: В последовательном колебательном контуре
• Анкор: лабораторная работа 6-1
• Дата: 21.12.2021
• Размер: 75.06 Kb.
• Имя файла: лр 6-1.docx
• Тип: Лабораторная работа; #312021

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Омский государственный технический университет»
Кафедра физики

Отчёт

по лабораторной работе №6-1

ИЗУЧЕНИЕ ЯВЛЕНИЯ РЕЗОНАНСА

В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ


Выполнила:

студентка группы ЗТОП-201

Зубкова алёна

Проверил: Доц., К.Н. Постников Д.В.

Дата сдачи отчета:03.12.21
Омск-2021
Лабораторная работа 6-1
ИЗУЧЕНИЕ ЯВЛЕНИЯ РЕЗОНАНСА

В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы: изучить зависимость амплитуды напряжения на конденсаторе последовательного колебательного контура от частоты вынуждающей ЭДС; определить по результатам измерений параметры колебательного контура.

Приборы и принадлежности: работа выполняется на компьютере.

Краткая теория
Последовательный колебательный RLC-контур состоит из конденсатора емкостью С, катушки индуктивностью L, резистора сопротивлением R_м, включенных между собой последовательно (рис.1).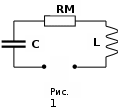

Для возбуждения вынужденных колебаний в контуре в него включен источник переменной вынуждающей ЭДС Е, изменяющейся по по закону:

Е = Е₀ sin t,

где Ω – циклическая частота колебаний вынуждающей ЭДС, Е₀– ее амплитуда.

Неоднородное дифференциальное уравнение, описывающее колебательный процесс в данном контуре:

(1)

где U – напряжение на конденсаторе,  - коэффициент затухания, ₀ - циклическая частота собственных колебаний контура, - коэффициент затухания.

Коэффициент затухания и циклическая частота собственных колебаний связаны с параметрами контура: R/2L=, ₀² = 1/LC.

Частное решение уравнения (1) имеет вид:

U = U_с sin (t +), (2)

где: 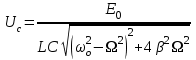, (3)

. (4)

U_с - амплитуда вынужденных колебаний напряжения на конденсаторе,  - сдвиг фаз колебаний напряжения на конденсаторе по отношению к колебаниям вынуждающей ЭДС.

Вынужденные колебания напряжения на конденсаторе происходят с частотой вынуждающей ЭДС .
Исследование зависимости амплитуды вынужденных колебаний напряжения на конденсаторе U_с от вынуждающей частоты  показывает:

- при   0 амплитуда напряжения на емкости U_с  Е₀;

- функция U_с = U_с () обладает максимумом U_сm при частоте генератора, называемой резонансной: ;

- при    амплитуда напряжения на емкости U_с  0.

Резкое увеличение амплитуды колебаний до максимального значения U_сm при частоте генератора _р называется резонансом. Зависимость амплитуды напряжения на емкости от частоты вынуждающей ЭДС носит название резонансной кривой. Положение и величина максимума резонансной кривой зависит от коэффициента затухания (рис.2). Выявление этих закономерностей – одна из задач построения кривых в данной работе.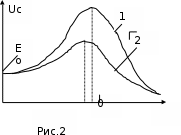

Для колебательного контура вводится понятие добротности, которая в работе может быть найдена как:

Q = U_сm /Е₀. (5)

Или

Q = 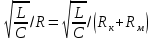, (6)

где R_к - некоторое эффективное сопротивление, учитывающее потери энергии в контуре, R_м – сопротивление резистора. Зная несколько значений сопротивлений резистора R_мi, поочередно включаемого в контур, можно определить величину R_к для каждого R_мi: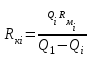

. (7)

Для данного контура выполняется условие:   ₀, при этом резонансная частота слабо зависит от коэффициента затухания и ее значение мало отличается от собственной циклической частоты:

_р  ₀ = 2n_pm, (8)

где n_pm – значение резонансной частоты.

Тогда индуктивность контура может быть вычислена:

L = 1/₀²C, (9)

при этом следует считать, что ₀ = 2n_pm0, где n_pm0 – значение резонансной частоты при R_м = 0 Ом.

Зная величину индуктивности и общее сопротивление контура, можно вычислить коэффициенты затухания по соотношению:

_i=(к> + R_мi)/2L, где i = 1, 2, 3, 4. (10)


Порядок выполнения работы

1. 
   Открыть диалоговое окно (щёлкнув дважды по «ярлык для резонанса» на рабочем столе), выбрать в меню «резонанс напряжения в RLC-контуре».
   
2. 
   Установить значение емкости контура (по указанию преподавателя), занести значения С и Е₀ в табл.1.
   

Таблица 1

	Е0 =				С =0,21Нфр
	Rм = 0 Ом		Rм = 100 Ом		Rм = 250 Ом
	n, кГц	Uс, В	n, кГц	Uс, В		n, кГц	Uс, В
1	80	1	80	1		80	1
2	85	1,5	85	1,5		85	1,5
3	90	1,7	90	1,7		90	1,7
4	95	2,5	95	2		95	2
5	100	2,5	100	2,3		100	2,3
6	105	5	105	5		105	3
7	107	16	107	8		107	5
8	110	5	110	6		110	4
9	115	2,5	115	2,5		115	1
10	120	2	120	2		120	1
npm,	107		107		107
кГц
Ucm,	16		8		5
В

3. 
   Получить изображения 3^х резонансных кривых, устанавливая поочередно значения R_м= 0, 100, 250 Ом и активируя «мышкой» клавишу «строить».
   
4. 
   Установить значение частот левой и правой границ в диапазоне примерно  10 кГц (или  20 кГц) от резонансной частоты , активируя режим масштабирования (кнопка с изображением увеличительного стекла). Занести значения U_c для 10 частот из диапазона масштабирования в табл.1. Для удобства определения значений можно поочередно работать с резонансной кривой при каждом значении R_м.
   
5. 
   Определить для каждой кривой (при каждом значении сопротивления резистора) уточненные значения резонансной частоты n_pm, при которой наблюдается резонанс напряжения на конденсаторе, и занести n_pm и соответствующие значения U_сm в табл.1.
   
6. 
   Построить резонансные кривые U_c = U_c(n) для каждого из сопротивлений и сделать выводы о наблюдаемых закономерностях.
   
7. 
   Вычислить для каждого значения R_м величину добротности по формуле (5) и соответствующие сопротивления контура R_к по формуле (7). Вычислить среднее значение сопротивления контура. Результаты занести в табл.2.
   

Таблица 2

№ опыта, i	Rм, Ом	Qi	RКi, Ом		L, Гн		 
1	0	16				671960	1,95Е+04
2	100	8	100	106,818182	2,73Е-03	671960	3,78Е+0,4
3	250	2	113,64			671960	6,53Е+04